标题

NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis, link

期刊

ECCV, 2020, 1432 citations. arxiv link, arxiv pdf link

后来又被期刊Communications of the ACM收录，pdf link, website link

Project link: https://www.matthewtancik.com/nerf

贡献

使用MLP学习三维场景中的隐含形式，给定100张场景中的视角图片训练模型，通过体渲染的方式获取新视角下的图像。

公式解读

突破性理解的笔记

- 是这样：从原点$\mathbf{o}$出发，沿着方向$\mathbf{d}$，移动速度是$\mathbf{d}$，移动时间是t，得到的射线。
- $r(t)$ 表示在$t$（可以理解为移动的时间，也可以理解为移动的比例）的位置。
- $C(\mathbf{r})$表示的是沿着射线r，从$t_n$到$t_f$这段路径中获取到的颜色。
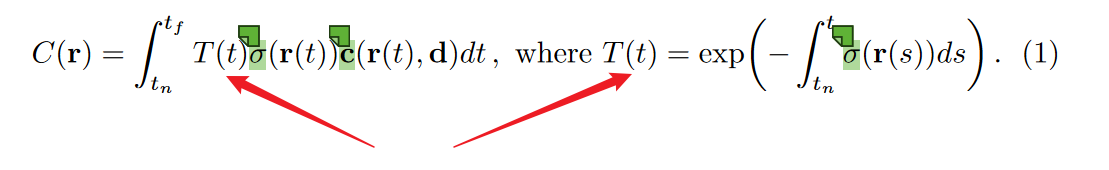
- $T(t)$表示的是，一条光线想要成功从t传播回到$t_n$是需要路上干干净净的，如果路上不干净，有一些东西挡着它，就无法顺利的传播回来。
- $\int_{t_n}^{t}\sigma (\mathbf{r}(s))ds$表示从$t_n$到$t$这段路上有多少人进行遮挡，数值越大，遮挡的程度越高。
- $-\int_{t_n}^{t}\sigma (\mathbf{r}(s))ds$，与不加负号的时候相反，遮挡的越多，数值越小，表示的是通过程度。遮挡越多，通过程度越高；遮挡越少，通过程度越高。不过这是一个负数，要给他变到正数上去。
- $exp\left(-\int_{t_n}^{t}\sigma (\mathbf{r}(s))ds\right)$ ，是从$t_n$到$t$的通过程度。这时候，该数值已经是0到1之间的浮点数了，可以理解为概率。
- $T(t)$，因此就表示为光线顺利通过的路径概率，路径的起点是$t_n$,终点是$t$。
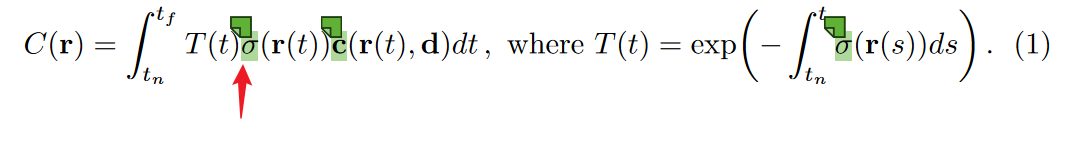
- 路径上每个地方都有粒子、物品在发光，发光的粒子越多，最后呈现出来的光就越亮。
- $\sigma(\mathbf{r}(t))$表示的是在t所对应的位置，发光粒子的数量。
- 最后，每个位置的发光粒子，发的光颜色是不一样的。
- $\mathbf{c}(\mathbf{r}(t), \mathbf{d}(t))$表示这个粒子所体现的颜色值，注意这个颜色值是矢量，代表它至少是RGB三通道的，每个通道都可以积分。

连续积分不容易处理，使用离散采样求和的方法，逼近连续积分的精确数值。

- $\delta_{j}$ 表示移动的距离
- 积分形式的离散化求和表示而已。
- 由于原始式子的不可微性，通过alpha组合的方式，转换为可微的新形式。
- 与$\sigma_{i}$ 是成正向相关的。$\sigma_{i}$ 越大，该项的数值越大。而且，是一个0-1之间的数值。表示这段区域内的占有体积的比率。