标题
Volume Rendering of Neural Implicit Surfaces
2021, NIPS, 95 citations. 是2021年NIPS的Oral。
作者
Lior Yariv$^1$ Jiatao Gu$^2$ Yoni Kasten$^1$ Yaron Lipman$^{1,2}$
$^1$Weizmann Institute of Science
$^2$Facebook AI Research
Weizmann科学研究所的作品,是另一篇IDR,原班人马的续作。Weizmann科学研究所位于以色列,被誉为是除美国之外最适合科研的场所之一。这个研究所的内容以数学功底见长,本篇论文中使用数学慢慢证明出一个误差上界,采用迭代的方式降低误差界,以获得物体表面处的采样值。
链接
论文链接:
论文的Peer Reviews:
-
值得注意的是,这篇文章的Peer Review评分很高。
-
Rating: 9, 9, 7, 9
-
Confidence: 4, 3, 5, 4
代码实现:
-
官方GitHub版本。VolSDF GitHub
-
在GitHub上找到一个非官方的个人实现版本。 Neurecon GitHub。
-
数据集链接来自论文的项目网站,约2GB。Data Link
相关知识链接:
-
文章中,提到朗博表面、非朗博表面。
-
学习参考链接:表面辐射特性 Blog
-
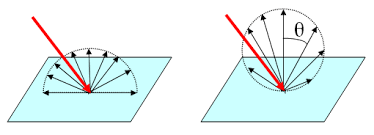
学习总结:朗博表面是一种高度理想化的表面,这种表面不吸收任何入射光,均匀的向各个方向反射,反射的辐射强度(radiance intensity, I)是随表面法线之间的夹角余弦值变化的。辐照度(radiance, L)是各个方向上相同的。
-
-
图左为辐射强度,图右为辐照度。
Open Review Ratings
| Time Spent Reviewing | Rating | Confidence |
|---|---|---|
| 3.5 | 9 | 4 |
| 6 | 9 | 3 |
| 4 | 7 | 5 |
| 7 | 9 | 4 |
要点
目的
针对NeRF重建物体表面比较粗糙的问题,目的是实现平滑性好、伪影少的重建模型。
除此之外,通过引入SDF的约束,让两个分支网络——空间占有率网络和空间颜色网络,实现表面渲染过程中二者的解构。
思想
从两条思路进行改进。一是原NeRF并不对密度场进行显式约束,因而采用有符号距离函数作为重建的约束条件;二是NeRF的采样算法不够完善,针对光路径上的离散化积分策略进行改进。
-
使用SDF约束体密度。
-
设计光路采样算法。
方法
-
SDF约束体密度。
-
采用Laplace密度函数作为体密度的估计值,函数的输入是有符号距离函数值,函数的输出乘以$\alpha$倍就得到体密度。
-
与Laplace的密度函数相关的体密度为:
-
迭代采样策略。
-
首先均匀采样,得到采样点$\mathcal{T}$。
-
根据采样点估计误差上界。如果误差上界不满足误差下限$\varepsilon$,或者达到迭代最多次数,就终止循环。
-
开始循环
-
增加采样个数,使得误差小于下界$\varepsilon$。
-
在新的采样情况下,降低$\beta$的数值。
-
根据采样的情况,估计空间中的体密度分布状况。
-
根据空间中的体密度分布情况,获取最终的采样值。渲染。
公式证明
定理1的证明
附录中定理1的证明

最后一个不等式,其实就是下面的式子,右边就是利普西斯常数的上界了。
\[\begin{align} &\vert\sigma(x(s)) - \sigma(x(t))\vert\\ \leq&\alpha \vert s - t \vert \dfrac{1}{2\beta}exp\left(- \dfrac{\vert s \vert}{\beta}\right)\\ = &\vert s - t \vert \dfrac{\alpha}{2\beta} exp(-\dfrac{\vert s \vert}{\beta}) \end{align}\]想法
优点
- 优化采样策略估计体密度分布。不过这样真的有效吗?
缺点
- From Paper Conclusions
First, although working well in practice, we do not have a proof of correctness for the sampling algorithm. We believe providing such a proof, or finding a version of this algorithm that has a proof would be a useful contribution. In general, we believe working with bounds in volume rendering could improve learning and disentanglement and push the field forward.
实际效果很好,但是没有采样算法正确性的证明。假设在体渲染的时候,处于体的边界会对学习和解构有所提升。
- From Paper Conclusions
Second, representing non-watertight manifolds and/or manifolds with boundaries, such as zero thickness surfaces, is not possible with an SDF. Generalizations such as multiple implicits and unsigned fields could be proven valuable.
对于非密闭的流形,或者有边界的流形来说,(例如比较细、比较薄的表面),不能使用SDF进行表达。多种隐表示的泛化以及无符号场可能会是有效的。
- From Paper Conclusions
Third, our current formulation assumes homogeneous density; extending it to more general density models would allow representing a broader class of geometries.
目前的公式假设存在同质的密度,将这个扩展到更加一般化的密度模型,有可能可以表达更大范围的几何物体类别。
Eikonal Loss的作用在于让SDF的梯度接近于1,也就是SDF的变化是均匀的,意味着物体的密度变化是均匀的,而无法考虑物体的密度变化,比如在烟雾或者水体、玻璃等场景中的变化情况。如果需要估计场景中的密度值,就不应该在全局中使用Eikonal Loss。
- From Paper Conclusions
Fourth, now that high quality geometries can be learned in an unsupervised manner it will be interesting to learn dynamic geometries and shape spaces directly from collections of images.
高质量的几何结构可以用无监督的方式学习得到,有可能直接从图像中学习到动态几何空间和形状空间。
后续要读的文章
-
同期的另一篇隐式表面重建工作。UniSURF
-
2022年的解构几何形状和物体表面的工作。NeuMesh
-
NeRF的改进工作,在文中用于做比对。NeRF++
-
从点云重建物体mesh。Poisson Surface Reconstruction, 2006
-
多视图几何,从图像生成多幅深度图,最后融合成点云。ColMAP. [Pixelwise view selection for unstructured multi-view stereo.]
-
在NeuS中也见到过,不确定这是约束什么的。Eikonal loss. [Multiview neural surface reconstruction by disentangling geometry and appearance.], [Implicit geometric regularization for learning shapes.]
-
体密度定义的来源。Optical models for direct volume rendering.
-
IDR、BRDF都来自于这篇文章。BRDF的思想让VolSDF引入了渲染颜色时,依赖于水平集的梯度方向,也就是物体的表面朝向。IDR与VolSDF竟然是同一批作者,又是同一个工作的延展,可以,太可以了。IDR(Implicit Differentiable Render). BRDF(Bidirectional Reflectance Distribution Function). Multiview neural surface reconstruction by disentangling geometry and appearance.
-
DTU, BlendedMVS. 两个常见的NeRF数据集。DTU: [Large scale multi-view stereopsis evaluation.]. BlendedMVS: [Blendedmvs: A large-scale dataset for generalized multi-view stereo networks.].
-
COLMAP,似乎可以应对non-tightwater的物体表面重建问题。[Pixelwise view selection for unstructured multi-view stereo.]
-
Phase Transitions, Distance Functions, and Implicit Neural Representations. ICML 2021 Link
-
SAL: Sign Agnostic Learning of Shapes from Raw Data. VolSDF里面提到,神经网络的初始化,用的是这篇文章中的方法。SAL: Sign Agnostic Learning of Shapes from Raw Data
论文重点难点介绍
1. 研究背景与动机
-
背景:神经体积渲染(Neural Volume Rendering)近年来因其能够从稀疏输入图像合成新视图而受到关注。然而,现有的方法通常使用通用密度函数来表示场景几何,导致几何重建质量较差,通常存在噪声且保真度低。
-
动机:本文提出了一种新的方法(VolSDF),通过将体积密度表示为几何的函数,而不是将几何表示为密度的函数,从而改善神经体积渲染中的几何表示和重建质量。
2. 方法核心:VolSDF
- 密度表示:VolSDF将体积密度$\sigma(x)$定义为拉普拉斯累积分布函数(CDF)应用于符号距离函数(SDF)表示的结果,即:
其中,$\alpha$和$\beta$是可学习参数,$\Psi_\beta$是拉普拉斯分布的CDF,$d_\Omega(x)$是符号距离函数。
- 优势:
-
提供几何学习的归纳偏置,便于分离密度和辐射场。
-
通过误差界限,实现对视图射线的准确采样,从而精确耦合几何和辐射场。
-
实现形状和外观的高效无监督分离。
3. 体积渲染与采样
- 体积渲染积分:体积渲染的核心是计算沿射线的积分,以获取从相机位置$c$沿方向$v$的光线在路径上的累积辐射:
其中,$L$是辐射场,$\tau(t)$是概率密度函数(PDF),表示光线在路径上的衰减。
- 采样算法:VolSDF提出了一种基于误差界限的采样算法,通过迭代调整采样点和参数$\beta$,确保对不透明度的近似误差在给定阈值$\epsilon$内。算法通过以下步骤实现:
-
初始化均匀采样点集$T_0$。
-
根据误差界限选择初始$\beta^+$。
-
迭代上采样$T$,调整$\beta^+$,直到满足误差要求或达到最大迭代次数。
-
使用最终的$T$和$\beta^+$进行逆CDF采样。
4. 训练与损失函数
-
网络结构:VolSDF包含两个多层感知机(MLP):
-
$f_\phi(x)$用于近似SDF和全局几何特征$z$。
-
$L_\psi(x, n, v, z)$用于表示场景的辐射场。
-
损失函数:总损失由两部分组成:
其中,$L_{RGB}$是颜色损失,$L_{SDF}$是Eikonal损失,用于约束SDF的梯度接近1。
5. 实验结果
-
多视图3D重建:
-
在DTU数据集上,VolSDF在Chamfer距离上优于NeRF和COLMAP,与IDR相当,但无需使用物体掩码。
-
在BlendedMVS数据集上,VolSDF在Chamfer距离上显著优于NeRF++,同时保持了相似的PSNR值。
-
几何与外观分离:VolSDF能够成功分离几何和外观,通过交换不同场景的辐射场,实现形状和材质的切换,而NeRF则无法实现这一功能。
6. 难点与挑战
-
采样算法的理论保证:虽然采样算法在实践中表现良好,但目前缺乏严格的理论证明。
-
非封闭流形的表示:SDF无法表示非封闭流形或零厚度表面,需要进一步扩展到更通用的表示方法。
-
非均匀密度的建模:当前方法假设密度是均匀的,扩展到非均匀密度模型将有助于表示更广泛的几何形状。
7. 总结
VolSDF通过将体积密度表示为符号距离函数的变换,显著提高了神经体积渲染中的几何重建质量,并实现了几何与外观的有效分离。该方法在多视图3D重建任务中表现出色,同时为未来的研究提供了新的方向,例如动态几何学习和更复杂的密度建模。
论文详细讲解
1. 研究背景与动机
神经体积渲染(Neural Volume Rendering)近年来因其能够从稀疏输入图像合成新视图而受到广泛关注。然而,现有的方法通常将场景几何建模为通用密度函数,导致几何重建质量较差,通常存在噪声且保真度低。本文提出了一种新的方法(VolSDF),通过将体积密度表示为几何的函数,而不是将几何表示为密度的函数,从而改善神经体积渲染中的几何表示和重建质量。
2. 方法核心:VolSDF
2.1 密度表示
VolSDF的核心在于将体积密度$\sigma(x)$定义为符号距离函数(SDF)的变换形式:
\[\sigma(x) = \alpha \Psi_\beta(-d_\Omega(x))\]其中:
-
$d_\Omega(x)$是符号距离函数(SDF),表示点$x$到场景表面的有符号距离。
-
$\Psi_\beta$是拉普拉斯分布的累积分布函数(CDF),具体定义为:
- $\alpha$和$\beta$是可学习参数,控制密度的幅度和衰减速度。
这种表示方法有三个主要优势:
-
归纳偏置:通过SDF的零等值面自然定义几何表面,为几何学习提供有用的归纳偏置。
-
误差界限:允许对不透明度近似误差进行有效约束,从而实现对视图射线的准确采样。
-
分离形状和外观:通过SDF表示的密度能够高效地分离几何和外观,便于在不同场景之间切换形状和材质。
2.2 体积渲染与采样
体积渲染的核心是计算沿射线的积分,以获取从相机位置$c$沿方向$v$的光线在路径上的累积辐射:
\[I(c, v) = \int_0^\infty L(x(t), n(t), v) \tau(t) dt\]其中:
-
$L(x(t), n(t), v)$是辐射场,表示点$x(t)$在方向$v$上的辐射。
-
$\tau(t) = \sigma(x(t)) T(t)$是概率密度函数(PDF),表示光线在路径上的衰减。
-
$T(t) = \exp\left(-\int_0^t \sigma(x(s)) ds\right)$是透明度函数。
为了高效计算上述积分,VolSDF提出了一种基于误差界限的采样算法:
-
初始化采样点:从均匀采样点集$T_0$开始。
-
误差界限计算:根据定理1和定理2,计算不透明度近似误差的上界$B_{T,\beta}$。
-
迭代优化:通过迭代上采样和调整参数$\beta$,确保误差上界$B_{T,\beta} < \epsilon$,其中$\epsilon$是预设的误差阈值。
-
逆CDF采样:使用最终的采样点集$T$和参数$\beta$进行逆CDF采样,生成用于积分的样本点。
算法的核心在于通过误差界限动态调整采样点,从而在有限的采样预算下实现高精度的体积渲染。
2.3 训练与损失函数
VolSDF包含两个多层感知机(MLP):
-
几何网络:$f_\phi(x)$用于近似符号距离函数(SDF)和全局几何特征$z$。
-
辐射场网络:$L_\psi(x, n, v, z)$用于表示场景的辐射场。
总损失函数由两部分组成:
\[L(\theta) = L_{RGB}(\theta) + \lambda L_{SDF}(\phi)\]其中:
-
$L_{RGB}(\theta) = \mathbb{E}_p |I_p - \hat{I}_S(c_p, v_p)|_1$是颜色损失,用于优化渲染图像与真实图像之间的差异。
-
$L_{SDF}(\phi) = \mathbb{E}_z (|\nabla d(z)| - 1)^2$是Eikonal损失,用于约束SDF的梯度接近1,确保其符合符号距离函数的性质。
-
$\lambda$是超参数,用于平衡两种损失。
3. 实验结果
3.1 多视图3D重建
VolSDF在两个数据集上进行了评估:DTU数据集和BlendedMVS数据集。
-
DTU数据集:
-
VolSDF在Chamfer距离上优于NeRF和COLMAP,与IDR相当,但无需使用物体掩码。
-
在PSNR方面,VolSDF与NeRF相当,表明其在渲染质量上具有竞争力。
-
具体数值结果如下表所示:
| 方法 | Chamfer距离 (mm) | PSNR (dB) |
|---|---|---|
| NeRF | 1.89 | 30.65 |
| VolSDF | 0.86 | 30.38 |
| IDR | 0.90 | - |
-
BlendedMVS数据集:
-
VolSDF在Chamfer距离上显著优于NeRF++,同时保持了相似的PSNR值。
-
具体数值结果如下表所示:
| 方法 | Chamfer距离改善 (%) | PSNR (dB) |
|---|---|---|
| NeRF++ | - | 27.55 |
| VolSDF | 51.8 | 27.08 |
3.2 几何与外观分离
VolSDF能够成功分离几何和外观,通过交换不同场景的辐射场,实现形状和材质的切换。相比之下,NeRF无法实现这一功能,表明VolSDF在分离几何和外观方面具有显著优势。
4. 难点与挑战
尽管VolSDF在几何重建和渲染质量上取得了显著进展,但仍存在一些挑战:
-
采样算法的理论保证:虽然采样算法在实践中表现良好,但目前缺乏严格的理论证明。
-
非封闭流形的表示:SDF无法表示非封闭流形或零厚度表面,需要进一步扩展到更通用的表示方法。
-
非均匀密度的建模:当前方法假设密度是均匀的,扩展到非均匀密度模型将有助于表示更广泛的几何形状。
5. 总结
VolSDF通过将体积密度表示为符号距离函数的变换,显著提高了神经体积渲染中的几何重建质量,并实现了几何与外观的有效分离。该方法在多视图3D重建任务中表现出色,同时为未来的研究提供了新的方向,例如动态几何学习和更复杂的密度建模。
论文方法部分详解
3. 方法
本文提出了一种新的体积密度参数化方法,通过将密度表示为符号距离函数(SDF)的变换,从而改善神经体积渲染中的几何表示和重建质量。以下是方法部分的详细讲解:
3.1 密度作为变换后的SDF
符号距离函数(SDF)
设$\Omega \subset \mathbb{R}^3$表示场景中物体占据的空间,其边界为$M = \partial \Omega$。符号距离函数(SDF)$d_\Omega(x)$定义为:
\[d_\Omega(x) = (-1)^{1_\Omega(x)} \min_{y \in M} \|x - y\|\]其中,$1_\Omega(x)$是指示函数,当$x \in \Omega$时取值为1,否则为0。SDF的值为负时表示点在物体内部,为正时表示点在物体外部。
体积密度的定义
在神经体积渲染中,体积密度函数$\sigma: \mathbb{R}^3 \rightarrow \mathbb{R}^+$表示光在点$x$处的衰减率。本文提出将密度函数表示为SDF的变换形式:
\[\sigma(x) = \alpha \Psi_\beta(-d_\Omega(x))\]其中,$\alpha, \beta > 0$是可学习参数,$\Psi_\beta$是拉普拉斯分布的累积分布函数(CDF),具体定义为:
\[\Psi_\beta(s) = \begin{cases} \frac{1}{2} \exp\left(\frac{s}{\beta}\right) & \text{if } s \leq 0 \\ 1 - \frac{1}{2} \exp\left(-\frac{s}{\beta}\right) & \text{if } s > 0 \end{cases}\]密度函数的性质
当$\beta \rightarrow 0$时,密度函数$\sigma(x)$趋近于物体内部的常数密度$\alpha$,并在边界处平滑过渡到零。这种表示方式提供了以下优势:
-
几何的归纳偏置:通过SDF的零等值面自然定义几何表面,为几何学习提供有用的归纳偏置。
-
误差界限:允许对不透明度近似误差进行有效约束,从而实现对视图射线的准确采样。
-
分离形状和外观:通过SDF表示的密度能够高效地分离几何和外观。
3.2 体积渲染中的不透明度误差界限
体积渲染积分
体积渲染的核心是计算沿射线的积分,以获取从相机位置$c$沿方向$v$的光线在路径上的累积辐射:
\[I(c, v) = \int_0^\infty L(x(t), n(t), v) \tau(t) dt\]其中:
-
$L(x(t), n(t), v)$是辐射场,表示点$x(t)$在方向$v$上的辐射。
-
$\tau(t) = \sigma(x(t)) T(t)$是概率密度函数(PDF),表示光线在路径上的衰减。
-
$T(t) = \exp\left(-\int_0^t \sigma(x(s)) ds\right)$是透明度函数。
不透明度误差界限
为了高效计算上述积分,需要对不透明度$O(t) = 1 - T(t)$进行近似。本文提出了一种基于误差界限的采样算法,通过约束不透明度近似误差来确保采样的准确性。具体而言,对于一组采样点$T = {t_i}_{i=1}^n$,不透明度的近似误差$E(t)$可以表示为:
\[E(t) = \left|O(t) - \hat{O}(t)\right|\]其中,$\hat{O}(t)$是通过数值积分方法(如矩形法则)计算的近似不透明度。
通过定理1和定理2,本文推导出了不透明度误差的上界$B_{T,\beta}$,并证明了在足够密集的采样条件下,误差可以任意小。
3.3 采样算法
算法目标
采样算法的目标是通过有限的采样点集$T$,使得不透明度的近似误差满足预设的阈值$\epsilon$,即$B_{T,\beta} < \epsilon$。
算法步骤
-
初始化采样点:从均匀采样点集$T_0$开始。
-
误差界限计算:根据定理2,初始化参数$\beta^+$,使得误差上界$B_{T,\beta^+} \leq \epsilon$。
-
迭代优化:通过迭代上采样和调整参数$\beta^+$,逐步减小误差上界,直到满足$B_{T,\beta} \leq \epsilon$或达到最大迭代次数。具体步骤如下:
-
在每个迭代中,根据当前误差上界按比例增加采样点。
-
使用二分法搜索新的参数$\beta^$,使得$B_{T,\beta^} = \epsilon$。
- 逆CDF采样:使用最终的采样点集$T$和参数$\beta^+$进行逆CDF采样,生成用于积分的样本点。
算法的具体流程如下:
Algorithm 1: Sampling algorithm
Input: error threshold $\epsilon > 0$; $\beta$
1. Initialize $T = T_0$
2. Initialize $\beta^+$ such that $B_{T,\beta^+} \leq \epsilon$
3. while $B_{T,\beta} > \epsilon$ and not max_iter do
4. upsample $T$
5. if $B_{T,\beta^+} < \epsilon$ then
6. Find $\beta^* \in (\beta, \beta^+)$ such that $B_{T,\beta^*} = \epsilon$
7. Update $\beta^+ \leftarrow \beta^*$
8. end
9. end
10. Estimate $\hat{O}$ using $T$ and $\beta^+$
11. $S \leftarrow$ get fresh samples using $\hat{O}^{-1}$
12. return $S$
算法优势
该算法通过动态调整采样点和参数$\beta$,在有限的采样预算下实现了高精度的体积渲染。同时,该方法避免了传统方法中由于采样不足导致的几何和辐射场解耦问题。
3.4 训练
网络结构
VolSDF包含两个多层感知机(MLP):
-
几何网络:$f_\phi(x)$用于近似符号距离函数(SDF)和全局几何特征$z$,输出为$(d(x), z(x)) \in \mathbb{R}^{1+256}$。
-
辐射场网络:$L_\psi(x, n, v, z)$用于表示场景的辐射场,输出为$\mathbb{R}^3$。
此外,$\alpha$和$\beta$是全局可学习参数,且在实现中选择$\alpha = \beta^{-1}$。
损失函数
总损失函数由两部分组成:
\[L(\theta) = L_{RGB}(\theta) + \lambda L_{SDF}(\phi)\]其中:
-
$L_{RGB}(\theta) = \mathbb{E}_p |I_p - \hat{I}_S(c_p, v_p)|_1$是颜色损失,用于优化渲染图像与真实图像之间的差异。
-
$L_{SDF}(\phi) = \mathbb{E}_z (|\nabla d(z)| - 1)^2$是Eikonal损失,用于约束SDF的梯度接近1,确保其符合符号距离函数的性质。
-
$\lambda$是超参数,用于平衡两种损失。
训练细节
-
使用位置编码(positional encoding)对位置$x$和视图方向$v$进行编码,以捕捉高频细节。
-
使用像素级数据进行训练,每次训练使用1024个像素的批次。
-
超参数$\lambda$设置为0.1。
通过上述方法,VolSDF在神经体积渲染中实现了高质量的几何重建和外观表示,同时避免了传统方法中存在的问题。
论文定理详解
论文中定理的详细讲解
论文中提出了两个关键定理,用于分析和约束体积渲染中的不透明度近似误差。这些定理为采样算法的设计提供了理论基础。
定理 1:密度函数的导数界限
定理内容
对于体积密度函数 $\sigma(x) = \alpha \Psi_\beta(-d_\Omega(x))$,在射线 $x(t)$ 上的任意区间 $[t_i, t_{i+1}]$ 内,其导数满足:
\[\left|\frac{d}{ds} \sigma(x(s))\right| \leq \frac{\alpha}{2\beta} \exp\left(-\frac{d^\star_i}{\beta}\right)\]| 其中,$d^\star_i = \min_{s \in [t_i, t_{i+1}], y \notin B_i \cup B_{i+1}} |x(s) - y|$,且 $B_i = {x \mid |x - x(t_i)| < | d_\Omega(x(t_i)) | }$。 |
定理解释
-
符号距离函数的性质:
-
$d_\Omega(x)$ 是符号距离函数,表示点 $x$ 到表面 $M$ 的有符号距离。
-
$d^\star_i$ 是区间 $[t_i, t_{i+1}]$ 内点到表面的最小距离,反映了区间内点与表面的接近程度。
-
-
密度函数的导数:
-
密度函数 $\sigma(x)$ 是 SDF 的变换形式,其导数与 SDF 的梯度相关。
-
定理给出了密度函数导数的上界,该上界依赖于参数 $\alpha$、$\beta$ 和区间内点到表面的最小距离 $d^\star_i$。
-
-
物理意义:
-
当点靠近表面时($d^\star_i$ 较小),密度函数的变化率较大;远离表面时,变化率较小。
-
该定理为后续的不透明度误差分析提供了关键的数学工具。
-
定理 2:不透明度近似误差的上界
定理内容
对于射线 $x(t)$ 上的不透明度近似 $\hat{O}(t)$,其误差可以被上界约束为:
\[\left|\hat{O}(t) - O(t)\right| \leq \exp\left(-\int_0^t \sigma(x(s)) ds\right) \left[\exp\left(\sum_{i=1}^{k-1} \frac{\delta_i^2}{4\beta} \exp\left(-\frac{d^\star_i}{\beta}\right)\right) - 1\right]\]其中,$\delta_i = t_{i+1} - t_i$ 是采样点之间的间隔。
定理解释
-
误差来源:
-
不透明度 $O(t)$ 是通过积分密度函数得到的,而 $\hat{O}(t)$ 是通过数值方法(如矩形法则)近似得到的。
-
误差来源于数值积分的不精确性,尤其是在密度变化较快的区域(如表面附近)。
-
-
误差上界:
-
定理给出了不透明度近似误差的上界,该上界依赖于采样点的间隔 $\delta_i$ 和密度函数的导数界限。
-
通过定理 1,误差上界可以进一步表示为:
\[\left|\hat{O}(t) - O(t)\right| \leq \exp\left(-\int_0^t \sigma(x(s)) ds\right) \left[\exp\left(\sum_{i=1}^{k-1} \frac{\delta_i^2}{4\beta} \exp\left(-\frac{d^\star_i}{\beta}\right)\right) - 1\right]\]
-
-
物理意义:
-
误差上界表明,通过合理选择采样点和参数 $\beta$,可以有效控制不透明度的近似误差。
-
该定理为采样算法的设计提供了理论依据,确保在有限的采样点下实现高精度的体积渲染。
-
定理的应用
-
采样算法的设计:
-
通过定理 2,可以动态调整采样点的分布,使得不透明度的近似误差满足预设的阈值 $\epsilon$。
-
算法通过迭代优化采样点和参数 $\beta$,确保误差上界 $B_{T,\beta} < \epsilon$。
-
-
参数选择的指导:
-
定理 1 和定理 2 提供了参数 $\beta$ 的选择依据,通过调整 $\beta$ 可以平衡误差和计算效率。
-
当 $\beta$ 较小时,密度函数的变化率较大,需要更密集的采样点来控制误差。
-
通过这两个定理,论文为体积渲染中的不透明度近似误差提供了严格的理论分析,并基于此设计了高效的采样算法,从而显著提升了神经体积渲染的几何重建质量和渲染精度。
评论