标题
Volume Rendering of Neural Implicit Surfaces
2021, NIPS, 95 citations. 是2021年NIPS的Oral。
作者
Lior Yariv$^1$ Jiatao Gu$^2$ Yoni Kasten$^1$ Yaron Lipman$^{1,2}$
$^1$Weizmann Institute of Science
$^2$Facebook AI Research
Weizmann科学研究所的作品,是另一篇IDR,原班人马的续作。Weizmann科学研究所位于以色列,被誉为是除美国之外最适合科研的场所之一。这个研究所的内容以数学功底见长,本篇论文中使用数学慢慢证明出一个误差上界,采用迭代的方式降低误差界,以获得物体表面处的采样值。
链接
论文链接:
论文的Peer Reviews:
-
值得注意的是,这篇文章的Peer Review评分很高。
- Rating: 9, 9, 7, 9
- Confidence: 4, 3, 5, 4
代码实现:
-
官方GitHub版本。VolSDF GitHub
-
在GitHub上找到一个非官方的个人实现版本。 Neurecon GitHub。
-
数据集链接来自论文的项目网站,约2GB。Data Link
相关知识链接:
-
文章中,提到朗博表面、非朗博表面。
- 学习参考链接:表面辐射特性 Blog
- 学习总结:朗博表面是一种高度理想化的表面,这种表面不吸收任何入射光,均匀的向各个方向反射,反射的辐射强度(radiance intensity, I)是随表面法线之间的夹角余弦值变化的。辐照度(radiance, L)是各个方向上相同的。
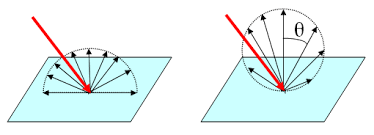
- 图左为辐射强度,图右为辐照度。
Open Review Ratings
| Time Spent Reviewing | Rating | Confidence |
|---|---|---|
| 3.5 | 9 | 4 |
| 6 | 9 | 3 |
| 4 | 7 | 5 |
| 7 | 9 | 4 |
要点
目的
针对NeRF重建物体表面比较粗糙的问题,目的是实现平滑性好、伪影少的重建模型。
除此之外,通过引入SDF的约束,让两个分支网络——空间占有率网络和空间颜色网络,实现表面渲染过程中二者的解构。
思想
从两条思路进行改进。一是原NeRF并不对密度场进行显式约束,因而采用有符号距离函数作为重建的约束条件;二是NeRF的采样算法不够完善,针对光路径上的离散化积分策略进行改进。
- 使用SDF约束体密度。
- 设计光路采样算法。
方法
-
SDF约束体密度。
-
采用Laplace密度函数作为体密度的估计值,函数的输入是有符号距离函数值,函数的输出乘以$\alpha$倍就得到体密度。
-
与Laplace的密度函数相关的体密度为: \(\begin{align} &\sigma(\mathbf{x}(t)) = \alpha\Psi_{\beta}(-d_{\Omega}(\mathbf{x}(t)))\\ &\Psi_{\beta}(x) = \begin{cases}\dfrac{1}{2}\exp(\dfrac{x}{\beta}) &\text{if}& x \leq 0 \\ 1-\dfrac{1}{2}\exp(-\dfrac{x}{\beta}) & \text{if} & x \gt 0 \end{cases}\\ &d_{\Omega}(\mathbf{x}) = (-1)^{\mathbf{1}_{\Omega}(\mathbf{x})}\min_{\mathbf{y}\in\mathcal{M}}\Vert x-y\Vert\\ &\mathbf{1}_{\Omega}(x) = \begin{cases}1 & \text{if} & x\in\Omega\\ 0 & \text{if} & x \notin \Omega \end{cases} \end{align}\)
-
-
迭代采样策略。
- 首先均匀采样,得到采样点$\mathcal{T}$。
- 根据采样点估计误差上界。如果误差上界不满足误差下限$\varepsilon$,或者达到迭代最多次数,就终止循环。
- 开始循环
- 增加采样个数,使得误差小于下界$\varepsilon$。
- 在新的采样情况下,降低$\beta$的数值。
- 根据采样的情况,估计空间中的体密度分布状况。
- 根据空间中的体密度分布情况,获取最终的采样值。渲染。
公式证明
定理1的证明
附录中定理1的证明

最后一个不等式,其实就是下面的式子,右边就是利普西斯常数的上界了。 \(\begin{align} &\vert\sigma(x(s)) - \sigma(x(t))\vert\\ \leq&\alpha \vert s - t \vert \dfrac{1}{2\beta}exp\left(- \dfrac{\vert s \vert}{\beta}\right)\\ = &\vert s - t \vert \dfrac{\alpha}{2\beta} exp(-\dfrac{\vert s \vert}{\beta}) \end{align}\)
想法
优点
- 优化采样策略估计体密度分布。不过这样真的有效吗?
缺点
- From Paper Conclusions
First, although working well in practice, we do not have a proof of correctness for the sampling algorithm. We believe providing such a proof, or finding a version of this algorithm that has a proof would be a useful contribution. In general, we believe working with bounds in volume rendering could improve learning and disentanglement and push the field forward.
实际效果很好,但是没有采样算法正确性的证明。假设在体渲染的时候,处于体的边界会对学习和解构有所提升。
- From Paper Conclusions
Second, representing non-watertight manifolds and/or manifolds with boundaries, such as zero thickness surfaces, is not possible with an SDF. Generalizations such as multiple implicits and unsigned fields could be proven valuable.
对于非密闭的流形,或者有边界的流形来说,(例如比较细、比较薄的表面),不能使用SDF进行表达。多种隐表示的泛化以及无符号场可能会是有效的。
- From Paper Conclusions
Third, our current formulation assumes homogeneous density; extending it to more general density models would allow representing a broader class of geometries.
目前的公式假设存在同质的密度,将这个扩展到更加一般化的密度模型,有可能可以表达更大范围的几何物体类别。
- From Paper Conclusions
Fourth, now that high quality geometries can be learned in an unsupervised manner it will be interesting to learn dynamic geometries and shape spaces directly from collections of images.
高质量的几何结构可以用无监督的方式学习得到,有可能直接从图像中学习到动态几何空间和形状空间。
后续要读的文章
- [ ] 同期的另一篇隐式表面重建工作。UniSURF
- [ ] 2022年的解构几何形状和物体表面的工作。NeuMesh
- [ ] NeRF的改进工作,在文中用于做比对。NeRF++
- [ ] 从点云重建物体mesh。Poisson Surface Reconstruction, 2006
- [ ] 多视图几何,从图像生成多幅深度图,最后融合成点云。ColMAP. [Pixelwise view selection for unstructured multi-view stereo.]
- [ ] 在NeuS中也见到过,不确定这是约束什么的。Eikonal loss. [Multiview neural surface reconstruction by disentangling geometry and appearance.], [Implicit geometric regularization for learning shapes.]
- [ ] 体密度定义的来源。Optical models for direct volume rendering.
- [ ] IDR、BRDF都来自于这篇文章。BRDF的思想让VolSDF引入了渲染颜色时,依赖于水平集的梯度方向,也就是物体的表面朝向。IDR与VolSDF竟然是同一批作者,又是同一个工作的延展,可以,太可以了。IDR(Implicit Differentiable Render). BRDF(Bidirectional Reflectance Distribution Function). Multiview neural surface reconstruction by disentangling geometry and appearance.
- [ ] DTU, BlendedMVS. 两个常见的NeRF数据集。DTU: [Large scale multi-view stereopsis evaluation.]. BlendedMVS: [Blendedmvs: A large-scale dataset for generalized multi-view stereo networks.].
- [ ] COLMAP,似乎可以应对non-tightwater的物体表面重建问题。[Pixelwise view selection for unstructured multi-view stereo.]
- [ ] Phase Transitions, Distance Functions, and Implicit Neural Representations. ICML 2021 Link
- [ ] SAL: Sign Agnostic Learning of Shapes from Raw Data. VolSDF里面提到,神经网络的初始化,用的是这篇文章中的方法。SAL: Sign Agnostic Learning of Shapes from Raw Data