论文链接

• Arxiv Link

• GitHub Page

发表日期：[v1] Tue, 11 Feb 2025 18:27:39 UTC (20,388 KB)（2025年2月11日）

重点难点分析

这篇论文介绍了一种名为 MeshSplats 的方法，旨在将基于高斯绘制（Gaussian Splatting, GS）的场景表示转换为网格（mesh）格式，从而结合光线追踪（ray tracing）技术的优势，提升渲染质量和效果。以下是论文的重点和难点的详细讲解：

论文重点

1. 问题背景与动机

• 高斯绘制（GS）的局限性：GS 是一种高效的 3D 场景表示方法，能够实现高质量的实时渲染，但其本质是基于栅格化的技术，难以处理复杂的光照效果（如阴影和反射）。

• MeshSplats 的目标：通过将 GS 转换为网格格式，利用光线追踪技术的优势（如处理非相干光线、实现阴影和反射效果），提升渲染质量。

2. MeshSplats 方法的核心思想

• GS 到网格的转换：MeshSplats 将 GS 中的高斯分布转换为网格面，保留了高斯的形状、颜色和透明度信息。

• 支持光线追踪：转换后的网格可以直接用于光线追踪渲染，从而实现高级光照效果。

• 优化流程：通过专用的优化算法进一步提升网格的几何精度和渲染质量。

3. 技术贡献

• 提出了一种将 GS 转换为网格的新方法，支持 2D 和 3D 高斯分布。

• 通过光线追踪实现了高级光照效果，如阴影和反射。

• 转换后的网格可以在传统渲染环境中使用（如 Blender 和 Nvdiffrast），无需专用的 GS 渲染器。

• 实验结果表明，MeshSplats 在渲染质量和几何精度上与 GS 相当，甚至在某些场景下表现更好。

4. 实验验证

• 在多个标准数据集（如 Mip-NeRF360、Tanks and Temples 和 Deep Blending）上进行了定量和定性评估。

• 与现有方法（如 3DGS、RaySplats 等）相比，MeshSplats 在某些数据集上表现更优，尤其是在处理复杂室内几何结构时。

• 优化流程显著提升了网格的几何精度和渲染质量，减少了伪影。

论文难点

1. GS 到网格的转换

• 难点：高斯分布是连续的数学模型，而网格是离散的几何表示。如何在转换过程中保留高斯的形状、颜色和透明度信息是一个挑战。

• 解决方案：论文提出了一种基于参数化的转换方法，通过控制缩放因子、三角形数量和透明度乘数等超参数，将高斯分布近似为网格面。

2. 网格优化

• 难点：转换后的网格可能存在伪影、几何细节丢失等问题，需要进一步优化。

• 解决方案：论文设计了一个优化流程，包括顶点位置、颜色和透明度的更新，以及冗余网格的剪枝。优化流程通过最小化损失函数（结合 L1 和 SSIM）来提升网格质量。

3. 渲染效率

• 难点：网格表示比高斯分布更复杂，可能导致渲染效率降低，尤其是在实时应用中。

• 解决方案：论文通过优化网格结构（如减少顶点数量）和利用高效的渲染工具（如 Nvdiffrast）来缓解这一问题。此外，使用扁平高斯（flat Gaussians）可以减少网格复杂度。

4. 光照效果的模拟

• 难点：虽然 MeshSplats 支持光线追踪，但如何在网格上实现与 GS 相当的光照效果（如反射和阴影）是一个挑战。

• 解决方案：论文通过在网格上应用光线追踪技术，并结合优化流程，实现了高级光照效果。然而，某些复杂场景（如透明表面的反射）仍然存在伪影。

总结

论文的核心贡献在于提出了一种将 GS 转换为网格的新方法，结合了 GS 的高效性和网格的灵活性，同时利用光线追踪技术提升了渲染质量。虽然在转换和优化过程中面临诸多挑战，但通过精心设计的算法和实验验证，MeshSplats 在多个数据集上取得了与 GS 相当甚至更好的效果。这种方法为计算机图形学中的渲染技术提供了一种新的思路，尤其是在处理复杂几何结构和高级光照效果时。

详细介绍

论文标题

MeshSplats: Mesh-Based Rendering with Gaussian Splatting Initialization

作者

Rafał Tobiasz, Grzegorz Wilczyński, Marcin Mazur, Sławomir Tadeja, Przemysław Spurek

1 摘要

背景：

Gaussian Splatting (GS) 是一种新兴的 3D 计算机图形技术，能够实现高质量的实时渲染。然而，GS 本质上是一种栅格化技术，无法直接利用光线追踪的优势，如处理阴影和反射等高级光照效果。

方法：

本文提出了一种名为 MeshSplats 的方法，将 GS 转换为网格（mesh）格式，从而可以利用光线追踪技术进行渲染。具体来说，MeshSplats 将高斯元素转换为网格面，保留了颜色和透明度信息。转换后的网格可以直接在现有的渲染环境中使用，如 Blender 和 Nvdiffrast。

贡献：

• 提出了一种将 GS 转换为网格的方法，支持光线追踪。

• 通过优化算法提升网格的几何精度和渲染质量。

• 实验证明，MeshSplats 在渲染质量和几何精度上与 GS 相当，甚至在某些场景下表现更好。

2 引言

背景：

在计算机图形学中，高效的 3D 对象表示至关重要。传统的网格表示方法虽然便于存储和快速渲染，但在直接从 2D 图像训练时存在挑战。GS 通过将 3D 场景表示为一组高斯分布来解决这一问题，但其本质上是栅格化技术，无法直接利用光线追踪的优势。

方法：

MeshSplats 通过将高斯元素转换为网格面，使得可以利用光线追踪技术进行渲染。具体步骤包括：

1. 使用 GS 创建一组高斯元素。

2. 将高斯元素转换为网格面，保留颜色和透明度信息。

3. 使用光线追踪技术渲染网格。

优势：

• 支持光线追踪，能够处理阴影和反射等高级光照效果。

• 可以在现有的渲染环境中使用，如 Blender 和 Nvdiffrast。

• 通过优化算法提升渲染质量。

3 相关工作

Neural Radiance Fields (NeRFs)：

NeRFs 通过隐式神经表示实现新视图合成，后续工作改进了渲染质量和效率。然而，这些方法通常计算量大，不适合实时应用。

Gaussian Splatting and Rendering Limitations：

GS 通过将场景表示为一组各向异性高斯分布来实现高效渲染。然而，这些方法依赖于球谐函数（SH）来近似视图依赖效果，导致在复杂光照下反射模糊。

Ray Tracing with Gaussian Representations：

最近的工作尝试将光线追踪与 GS 结合，以克服栅格化的限制。例如，3D Gaussian Ray Tracing (3DGRT) 使用包围高斯的边界原语，通过 GPU 加速光线追踪。然而，这些方法仍然依赖于自定义渲染器，限制了泛化能力。

Mesh-Based Rendering and Hybrid Approaches：

传统的网格表示方法便于光线追踪，但直接从图像优化网格存在挑战。MeshSplats 通过将 GS 转换为网格结构，结合了 GS 的优化优势和传统渲染器的兼容性。

4 MeshSplats 转换

核心步骤：

1. 使用 GS 创建一组高斯元素。

2. 将高斯元素转换为网格面，保留颜色和透明度信息。

3. 使用光线追踪技术渲染网格。

Gaussian Splatting：

GS 通过一组 3D 高斯分布表示 3D 场景，每个高斯元素由位置（均值）、协方差矩阵、透明度和颜色定义。颜色使用球谐函数（SH）表示，但也可以使用 RGB 颜色。

MeshSplats 转换 for Flat Gaussians：

• 每个高斯元素由均值、旋转矩阵和缩放参数定义。

• 通过计算椭圆的主轴和次轴，生成椭圆边界上的点，构造三角形网格。

• 颜色和透明度信息从高斯元素继承到网格顶点。

MeshSplats 转换 for 3D Gaussians：

• 类似于 2D 方法，但扩展到三维。

• 通过计算椭球的主轴，生成椭球边界上的点，构造三角形网格。

• 颜色和透明度信息从高斯元素继承到网格顶点。

Rendering MeshSplats in Nvdiffrast：

• 使用 Nvdiffrast 进行栅格化和深度剥离，管理透明度和重叠几何。

• 通过迭代渲染多个图层，确保每个图层正确合成。

Finetuning of MeshSplats：

• 优化流程包括顶点变换、栅格化、混合和损失计算。

• 损失函数是 L1 损失和结构相似性指数（SSIM）的加权组合。

• 优化过程中，顶点位置、颜色和透明度都会被更新，同时进行冗余网格的剪枝。

5 实验

数据集和指标：

• 数据集：Mip-NeRF360、Tanks and Temples、Deep Blending。

• 评估指标：PSNR、SSIM、LPIPS。

定量结果：

• 在 Mip-NeRF360 和 Tanks and Temples 数据集上，MeshSplats 的性能与现有方法相当。

• 在 Deep Blending 数据集上，MeshSplats 表现更优，证明了其在处理复杂室内几何结构和透明效果方面的有效性。

定性结果：

• 使用 Nvdiffrast 渲染的 MeshSplats 与 3DGS 的视觉质量几乎相同。

• 使用 Blender 的 EEVEE 渲染器，MeshSplats 也产生了高质量的渲染结果，尽管在某些细节上存在轻微的差异。

消融研究：

• 比较

• MeshSplats 可以与经典的 GS、2DGS 和 GaMeS 一起使用，但在处理复杂室内场景时，使用 2DGS 初始化的 MeshSplats 表现更优。

6 结论

总结：

MeshSplats 通过将 GS 转换为网格格式，成功地结合了 GS 的高效性和光线追踪的高级光照效果。实验结果表明，MeshSplats 在多个数据集上表现优异，尤其是在处理复杂室内几何结构和透明效果时。

局限性：

• 在处理大面积低纹理区域时，可能会出现几何碎片和透明度不一致的伪影。

• 使用 3DGS 初始化时，生成的网格过于密集，导致内存使用增加和渲染效率降低。

7 详细讲解

1 背景与动机

• 高斯溅射（Gaussian Splatting, GS）：GS 是一种新兴的 3D 计算机图形技术，通过将 3D 场景表示为一组高斯分布来实现高效渲染。每个高斯分布由位置（均值）、协方差矩阵、透明度和颜色定义。GS 能够实现高质量的实时渲染，但其本质上是栅格化技术，无法直接利用光线追踪的优势，如处理阴影和反射等高级光照效果。

• 光线追踪的优势：光线追踪能够处理非相干光线，实现高级光照效果，如阴影和反射。然而，传统的光线追踪方法通常需要网格表示，而直接从 2D 图像训练网格存在挑战。

2 MeshSplats 方法

• 核心思想：MeshSplats 通过将 GS 转换为网格格式，使得可以利用光线追踪技术进行渲染。具体来说，MeshSplats 将高斯元素转换为网格面，保留了颜色和透明度信息。转换后的网格可以直接在现有的渲染环境中使用，如 Blender 和 Nvdiffrast。

• 转换步骤：

1. 使用 GS 创建高斯元素：首先，使用 GS 创建一组高斯元素，每个元素由位置（均值）、协方差矩阵、透明度和颜色定义。

2. 将高斯元素转换为网格面：将每个高斯元素转换为网格面，保留颜色和透明度信息。对于扁平高斯（flat Gaussians），通过计算椭圆的主轴和次轴，生成椭圆边界上的点，构造三角形网格。对于 3D 高斯，通过计算椭球的主轴，生成椭球边界上的点，构造三角形网格。

3. 使用光线追踪技术渲染网格：将转换后的网格用于光线追踪渲染，实现高级光照效果。

3 技术贡献

• 将 GS 转换为网格：提出了一种将 GS 转换为网格的方法，支持 2D 和 3D 高斯分布。通过控制缩放因子、三角形数量和透明度乘数等超参数，将高斯分布近似为网格面。

• 支持光线追踪：转换后的网格可以直接用于光线追踪渲染，从而实现高级光照效果，如阴影和反射。

• 优化算法：通过专用的优化算法进一步提升网格的几何精度和渲染质量。优化流程包括顶点位置、颜色和透明度的更新，以及冗余网格的剪枝。

• 兼容传统渲染环境：转换后的网格可以在现有的渲染环境中使用，如 Blender 和 Nvdiffrast，无需专用的 GS 渲染器。

4 实验验证

• 数据集和指标：

• 数据集：Mip-NeRF360、Tanks and Temples、Deep Blending。

• 评估指标：PSNR（峰值信噪比）、SSIM（结构相似性指数）、LPIPS（感知图像补丁相似性）。

• 定量结果：

• 在 Mip-NeRF360 和 Tanks and Temples 数据集上，MeshSplats 的性能与现有方法相当，如 3DGS 和 RaySplats。

• 在 Deep Blending 数据集上，MeshSplats 表现更优，证明了其在处理复杂室内几何结构和透明效果方面的有效性。

• 定性结果：

• 使用 Nvdiffrast 渲染的 MeshSplats 与 3DGS 的视觉质量几乎相同，但在某些细节上表现更好。

• 使用 Blender 的 EEVEE 渲染器，MeshSplats 也产生了高质量的渲染结果，尽管在某些细节上存在轻微的差异。

• 消融研究：

• 比较了不同 GS 初始化方法（3DGS、2DGS、GaMeS）对 MeshSplats 性能的影响。结果表明，使用 2DGS 初始化的 MeshSplats 在处理复杂室内场景时表现更优。

5 结论与局限性

• 结论：MeshSplats 通过将 GS 转换为网格格式，成功地结合了 GS 的高效性和光线追踪的高级光照效果。实验结果表明，MeshSplats 在多个数据集上表现优异，尤其是在处理复杂室内几何结构和透明效果时。

• 局限性：

• 在处理大面积低纹理区域时，可能会出现几何碎片和透明度不一致的伪影。

• 使用 3DGS 初始化时，生成的网格过于密集，导致内存使用增加和渲染效率降低。

6 未来工作

• 改进网格优化算法：进一步优化网格结构，减少伪影，提升渲染质量。

• 提高渲染效率：探索更高效的渲染方法，减少内存使用，提高实时渲染性能。

• 扩展应用场景：将 MeshSplats 应用于更多的场景，如虚拟现实、增强现实等。

论文方法部分详细讲解

1 MeshSplats 转换方法

MeshSplats 的核心方法是将基于高斯溅射（Gaussian Splatting, GS）的表示转换为网格（mesh）格式，从而可以利用光线追踪技术进行渲染。具体来说，MeshSplats 通过以下三个主要步骤实现这一转换：

1. 使用 GS 创建高斯元素：

• 高斯元素的定义：每个高斯元素由位置（均值 \(m\)）、协方差矩阵 \(\Sigma\)、透明度 \(\sigma\) 和颜色 \(c\) 定义。颜色通常使用球谐函数（Spherical Harmonics, SH）表示，但在 MeshSplats 中使用 RGB 颜色以兼容传统的网格渲染器。

• GS 优化过程：通过迭代渲染和比较生成的图像与输入视图，优化高斯元素的参数。这一过程确保了高斯元素能够准确地表示 3D 场景。

2. 将高斯元素转换为网格面：

• 扁平高斯（Flat Gaussians）：

• 参数化：扁平高斯的协方差矩阵 \(\Sigma\) 被分解为旋转矩阵 \(R\) 和对角矩阵 \(S\)，其中 \(S = \text{diag}(s_1, s_2, s_3)\)，且 \(s_1 = \epsilon\)（一个非常小的值）。旋转矩阵 \(R\) 由列向量 \(r_1, r_2, r_3\) 组成。

• 网格生成：通过计算椭圆的主轴和次轴，生成椭圆边界上的点，构造三角形网格。具体步骤如下：

• 计算缩放后的旋转向量：

\[\text{scaled_rot1} = \text{scale_mul} \cdot \exp(s_2) \cdot r_2\] \[\text{scaled_rot2} = \text{scale_mul} \cdot \exp(s_3) \cdot r_3\]

• 生成椭圆边界上的点：

\[v_i = m + \cos(\theta_i) \cdot \text{scaled_rot1} + \sin(\theta_i) \cdot \text{scaled_rot2}\]

其中 \(\theta_i\) 是均匀分布在 \([-π, π]\) 范围内的角度。

• 构造三角形网格：将所有点连接成一个三角形扇形，每个三角形共享椭圆中心点。

• 颜色和透明度：每个顶点的颜色和透明度从对应的高斯元素继承。边界顶点的透明度通过乘以一个透明度乘数（opac_mul）来创建线性插值。

• 3D 高斯（3D Gaussians）：

• 参数化：3D 高斯的协方差矩阵 \(\Sigma\) 被分解为旋转矩阵 \(R\) 和对角矩阵 \(S\)，其中 \(S = \text{diag}(s_1, s_2, s_3)\)。

• 网格生成：通过计算椭球的主轴，生成椭球边界上的点，构造三角形网格。具体步骤如下：

• 计算缩放后的旋转向量：

\[\text{scaled_rot1} = \text{scale_mul} \cdot \exp(s_1) \cdot r_1\] \[\text{scaled_rot2} = \text{scale_mul} \cdot \exp(s_2) \cdot r_2\] \[\text{scaled_rot3} = \text{scale_mul} \cdot \exp(s_3) \cdot r_3\]

• 生成椭球边界上的点：

\[v_i = m + \cos(\theta_i) \cdot \text{scaled_rota} + \sin(\theta_i) \cdot \text{scaled_rotb}\]

其中 \(\text{scaled_rota}\) 和 \(\text{scaled_rotb}\) 是定义当前表面的向量对。

• 构造三角形网格：将所有点连接成一个三角形扇形，每个三角形共享椭球中心点。

• 颜色和透明度：每个顶点的颜色和透明度从对应的高斯元素继承。边界顶点的透明度通过乘以一个透明度乘数（opac_mul）来创建线性插值。

3. 使用光线追踪技术渲染网格：

• Nvdiffrast 渲染：

• 顶点变换：使用模型-视图-投影（MVP）矩阵将 3D 顶点变换到 2D 屏幕空间。

• 栅格化和混合：使用深度剥离技术管理透明度和重叠几何。通过迭代渲染多个图层，确保每个图层正确合成。

• 损失函数：优化过程中使用 L1 损失和结构相似性指数（SSIM）的加权组合：

\[L = \lambda \cdot L1(\hat{y}, y) + (1 - \lambda) \cdot SSIM(\hat{y}, y)\]

其中 \(y\) 是真实图像，\(\hat{y}\) 是预测图像，\(\lambda = 0.6\) 是平衡常数。

• 优化和剪枝：优化过程中更新顶点位置、颜色和透明度。每 10 个 epoch 进行一次剪枝，移除透明度低于阈值的冗余面和顶点。

2 优化算法

MeshSplats 的优化算法旨在提升网格的几何精度和渲染质量。具体步骤如下：

1. 顶点变换：

• 使用 MVP 矩阵将 3D 顶点变换到 2D 图像空间：

\[v_{\text{transformed}} = \text{MVP} \cdot v_i\]

2. 栅格化和混合：

• 使用深度剥离技术管理透明度和重叠几何。通过迭代渲染多个图层，确保每个图层正确合成。

3. 损失函数：

• 优化过程中使用 L1 损失和结构相似性指数（SSIM）的加权组合：

\[L = \lambda \cdot L1(\hat{y}, y) + (1 - \lambda) \cdot SSIM(\hat{y}, y)\]

其中 \(y\) 是真实图像，\(\hat{y}\) 是预测图像，\(\lambda = 0.6\) 是平衡常数。

4. 优化和剪枝：

• 优化过程中更新顶点位置、颜色和透明度。顶点位置的更新使用较小的学习率 \(\text{lr}_{\text{verts}} = \exp(-3) \cdot \text{lr}_{\text{color}}\)，以确保位置更新的稳定性和细微性。

• 每 10 个 epoch 进行一次剪枝，移除透明度低于阈值的冗余面和顶点。这有助于减少内存使用和计算复杂度，同时保持场景表示的保真度。

3 实验验证

MeshSplats 的方法在多个标准数据集上进行了验证，包括 Mip-NeRF360、Tanks and Temples 和 Deep Blending。实验结果表明，MeshSplats 在渲染质量和几何精度上与现有的基于栅格化的技术相当，甚至在某些场景下表现更好。具体来说：

• 定量结果：

• 在 Mip-NeRF360 和 Tanks and Temples 数据集上，MeshSplats 的性能与 3DGS 和 RaySplats 等方法相当。

• 在 Deep Blending 数据集上，MeshSplats 表现更优，证明了其在处理复杂室内几何结构和透明效果方面的有效性。

• 定性结果：

• 使用 Nvdiffrast 渲染的 MeshSplats 与 3DGS 的视觉质量几乎相同，但在某些细节上表现更好。

• 使用 Blender 的 EEVEE 渲染器，MeshSplats 也产生了高质量的渲染结果，尽管在某些细节上存在轻微的差异。

4 消融研究

MeshSplats 的消融研究比较了不同 GS 初始化方法（3DGS、2DGS、GaMeS）对性能的影响。结果表明：

• 3DGS 初始化：在所有数据集上性能有所下降，主要是因为 3D 高斯与网格结构的拟合较为复杂。

• GaMeS 初始化：在 Mip-NeRF360 和 Deep Blending 数据集上表现与 RGB 对应方法相当，表明在几何保真度方面有效。

• 2DGS 初始化：在 Deep Blending 数据集上表现更优，证明了其在处理复杂室内场景时的有效性。

5 结论

MeshSplats 通过将 GS 转换为网格格式，成功地结合了 GS 的高效性和光线追踪的高级光照效果。实验结果表明，MeshSplats 在多个数据集上表现优异，尤其是在处理复杂室内几何结构和透明效果时。尽管在处理大面积低纹理区域时可能会出现伪影，但通过优化算法可以显著提升网格的几何精度和渲染质量。

原文翻译

MeshSplats：基于网格的渲染与高斯绘制初始化

Rafał Tobiasz¹ Grzegorz Wilczyński¹ Marcin Mazur¹ Sławomir Tadeja² Przemysław Spurek¹

摘要

高斯绘制（Gaussian Splatting, GS）是 3D 计算机图形学中一种新兴且关键的技术。基于 GS 的算法几乎总是绕过传统的光线追踪等方法，而光线追踪在渲染中具有许多固有的优势。例如，光线追踪能够处理非相干光线，以实现高级光照效果，包括阴影和反射。为了克服这一局限性，我们提出了 MeshSplats，这是一种将 GS 转换为网格格式的方法。在完成训练后，MeshSplats 将高斯元素转换为网格面，从而可以利用光线追踪方法及其所有相关优势进行渲染。我们的模型可以在转换后立即使用，生成的网格质量略有降低，无需额外训练。此外，我们可以通过应用专门的优化算法进一步提升重建质量，该算法作用于网格面而非高斯组件。我们的方法通过实验结果得到了验证，突显了其在计算机图形学和图像处理中的广泛应用潜力。源代码可在以下链接获取：https://github.com/gwilczynski95/meshsplats。

1 引言

在计算机图形学领域，高效表示 3D 对象至关重要。传统技术使用网格进行便捷存储和快速渲染（Foley 等人，1994）。此外，基于网格表示的各种光线追踪方法能够实现多种优势，例如处理非相干光线以实现次级光照效果，包括阴影和反射（Peddie，2019）。

不幸的是，直接在 2D 图像上训练网格表示存在显著挑战。高斯绘制（GS）框架（Kerbl 等人，2023）通过将 3D 场景表示为一组高斯分布来解决这一问题，这些高斯分布由均值、协方差、透明度和颜色等参数定义，通常用球谐函数表示。这种表示可以有效训练以实现高质量重建和实时渲染。然而，需要注意的是，GS 本质上是一种栅格化技术，使用高斯投影而非光线追踪。这一特性使得 GS 在尝试整合光照、阴影或反射效果时面临挑战（Kerbl 等人，2023；Moenne-Loccoz 等人，2024），因为栅格化和光线追踪之间存在关键差异。通常，前者通过近似图像的形成来实现实时性能，而后者则能够实现全面且高质量的渲染，但通常基于网格表示。

一种潜在的解决方案是将 GS 训练与光线追踪相结合，这种方法被称为三维高斯光线追踪（3D Gaussian Ray Tracing, 3DGRT）（Moenne-Loccoz 等人，2024）。该方法产生了出色的视觉效果，包括光线反射和阴影。此外，它还能够将 3D 场景与基于网格的模型整合。3DGRT 使用包围每个高斯的边界原语，并在这些原语上高效应用光线追踪模型，而不是直接作用于高斯。在 RaySplat（Byrski 等人，2025）中，作者使用椭圆作为高斯的近似替代品，而不是边界原语。上述方法采用光线追踪进行渲染，能够模拟光照效果，但需要专用的渲染环境。LinPrim（von Lützow & Nießner，2025）使用八面体和四面体等线性原语进行可微分体积渲染。该方法使用基于网格的原语而非高斯分布，能够生成高质量的渲染结果。然而，它需要专用的训练和渲染环境。

图1. MeshSplats（我们的方法）促进了将高斯泼溅（Gaussian Splatting）转换为网格格式的过程，随后可以使用Blender和Nvdiffrast等主流工具进行渲染。这种转换使得复杂的照明效果（如反射和阴影）成为可能，并能够执行基于网格的模拟。

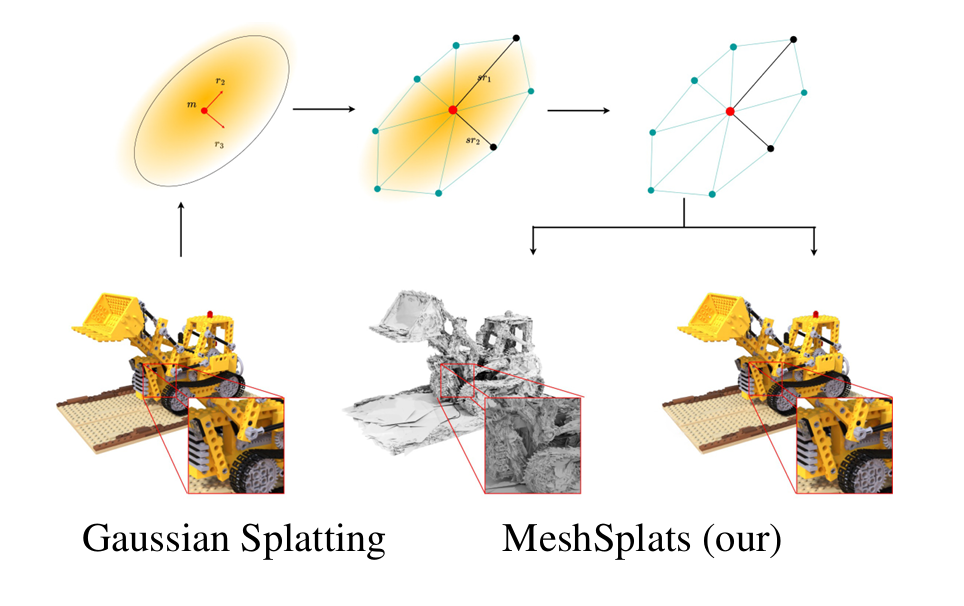
图2. MeshSplats（我们的方法）将平面高斯转换为网格的过程，其中\(m\)是高斯的均值，\(r_2\)和\(r_3\)是旋转矩阵\(R\)的第二和第三列（见公式(1)），而\(sr_1\)和\(sr_2\)表示公式(3)中的缩放旋转1和缩放旋转2。

为了解决这些问题，我们提出了 MeshSplats，这是一种直接将高斯组件转换为网格格式的方法，可以在现有的渲染环境中使用，例如 Blender¹ 或 Nvdiffrast²（Munkberg 等人，2022）（见图1）。具体来说，我们首先获得一组带有颜色和透明度的不相交网格（见图2）。接下来，我们使用光线追踪在基于网格的表示上渲染带有光照效果的对象。在这一过程中，原始 GS 的主要组成部分是粒子的透明度。为此，我们使用了 Nvdiffrast，这是一个 PyTorch 库，用于基于栅格化的可微分渲染的高性能原语操作。我们采用这种方法是因为它能够高效地渲染由 GS 导出的网格。然而，值得注意的是，也可以使用 Blender 等替代渲染器，尽管由于 GS 技术中透明度的重要性，输出质量会受到限制（见图1）。

MeshSplats 技术专注于扁平高斯分布，这些高斯分布具有单一的缩放参数。这些高斯分布能够进行有效的训练，并能够达到相当的渲染质量。此外，扁平高斯的形态与网格相似，因此将其转换为网格面比传统三维高斯分布更为直接。因此，尽管使用扁平高斯可能会在效率上有所妥协，但它们与 MeshSplats 的结合是可行的。

图3. MeshSplats（我们的方法）生成的渲染示例，使用Blender或Nvdiffrast应用了照明条件和网格变形。渲染对象展示了各种照明效果，其中顶部中间的渲染展示了一个具有混合纹理的对象。原始图像（未在此展示）来自NeRF Synthetic数据集。

此外，我们提出的方法将 GS 转换为网格以促进直接渲染。因此，为了生成高质量的重建，我们可以使用基于网格的 GS 方法，而不是传统的高斯分布来提高质量。这使得我们的方法能够与光照和阴影效果整合（见图3）。

总结来说，我们的工作贡献如下：

• 我们提出了 MeshSplats，这是一种将带有扁平高斯分布的 GS 转换为基于网格的表示的新方法，允许进一步整合专用工具；

• MeshSplats 使用光线追踪，能够处理非相干光线以实现次级光照效果，例如从高度失真相机渲染的阴影和反射；

• MeshSplats 可以在传统的渲染环境中使用，从而无需使用专用的 GS 渲染器；

• 我们的定量和定性实验结果证实，MeshSplats 达到了与高斯绘制相当的渲染质量，同时具备基于网格表示的优势；

• 我们展示了 MeshSplats 的优化流程能够有效减少伪影并细化几何细节，从而提升几何精度和逼真渲染效果。

2 相关工作

我们的工作在高斯绘制（GS）的最新进展与经典的基于光线追踪的渲染技术之间建立了联系，同时解决了以栅格化为中心的方法的局限性。在这里，我们从四个主要领域回顾相关文献。

神经辐射场与视图依赖效果

神经辐射场（NeRFs）（Mildenhall 等人，2021）通过将场景建模为隐式的神经表示，彻底改变了新视图合成领域。后续的研究在渲染质量和效率方面取得了进步（Barron 等人，2021；2022；2023），而像 Ref-NeRF（Verbin 等人，2022）和 SpecNeRF（Ma 等人，2024）这样的方法则利用反射方向和高斯编码增强了视图依赖效果。NeRF-Casting（Verbin 等人，2024）引入了沿反射路径的光线行进，用于实现逼真的近场照明，但这些方法仍然计算量大，不适合实时应用。相比之下，基于 GS 的方法能够实现实时渲染，但在处理反射和阴影时缺乏细致的处理。

高斯绘制与渲染局限性

三维高斯绘制（3DGS）（Kerbl 等人，2023）是一个突破，它通过可微分栅格化优化的各向异性高斯分布来表示场景。扩展方法如 Mip-Splatting（Yu 等人，2024）减少了锯齿现象，而二维高斯绘制（2DGS）（Huang 等人，2024）通过将高斯限制在二维流形上改善了表面对齐。然而，这些方法依赖于球谐函数（SH）来近似视图依赖效果，在复杂光照下会导致反射模糊。最近的研究，如 GaussianShader（Jiang 等人，2024）和 3DGS-DR（Ye 等人，2024），引入了环境贴图用于反射，但仅限于远距离光照。3iGS（Tang 和 Cham，2025）通过张量分解引入了光照场，但对场景的有界假设限制了其在现实世界中的应用。至关重要的是，所有这些方法都依赖于栅格化，而栅格化在处理阴影和互反射等高级效果所需的非相干光线时存在困难。

高斯表示与光线追踪

最近的研究将光线追踪与 GS 结合起来，以克服栅格化的局限性。三维高斯光线追踪（3DGRT）（Moenne-Loccoz 等人，2024）通过在高斯周围使用边界原语，利用 NVIDIA OptiX（Parker 等人，2010）实现了 GPU 加速的光线追踪。尽管效率很高，但 3DGRT 将高斯近似为多面体，这使得其与扁平高斯（Huang 等人，2024）和非高斯分布的兼容性变得困难。EnvGS（Xie 等人，2024）引入了环境高斯用于建模反射，但仍然限于 GS 特定的渲染管线。类似地，IRGS（Gu 等人，2024）提出了用于逆向渲染的可微分二维高斯光线追踪，但需要复杂的蒙特卡洛采样。这些方法突出了光线追踪的潜力，同时也继承了 GS 的结构局限性，例如对自定义渲染器的依赖以及阻碍泛化的近似方法。

基于网格的渲染与混合方法

经典的网格表示有助于高效的光线追踪，但直接从图像优化网格存在挑战。我们的工作通过将 GS 转换为类似网格的结构来填补这一空白，利用 GS 的优化优势，同时保持与传统渲染器（如 Blender 和 Nvdiffrast（Munkberg 等人，2022））的兼容性。与多面体近似（Moenne-Loccoz 等人，2024）不同，我们的方法通过将扁平高斯映射到网格面上来保留几何保真度，从而避免了边界原语带来的伪影。这种方法类似于网格绘制技术（Weyrich 等人，2007），但强调的是训练后的转换，而不是直接的网格优化。

3 MeshSplats 转换

图2. MeshSplats（我们的方法）将平面高斯转换为网格的过程，其中\(m\)是高斯的均值，\(r_2\)和\(r_3\)是旋转矩阵\(R\)的第二和第三列（见公式(1)），而\(sr_1\)和\(sr_2\)表示公式(3)中的缩放旋转1和缩放旋转2。

我们方法的核心包括三个简单的步骤。首先，我们使用经典的高斯绘制（GS）创建一组高斯分布。接下来，我们应用 MeshSplats 将高斯元素转换为独立的网格面，这些网格面近似高斯的形状，同时保留颜色和透明度。这一步可以得到高质量的重建，尽管仍可能有轻微的伪影。最后，我们类似于 GS 的方式，通过独立的网格面而不是高斯组件来优化这种表示。MeshSplats 转换的示意图如图2 所示。

以下，我们详细描述我们的方法。我们首先回顾传统的 GS 技术，然后介绍 MeshSplats 的参数化。我们的模型旨在处理一般的高斯分布，特别强调其对扁平高斯的适用性。因此，我们将专注于扁平高斯，然后扩展到三维高斯。我们进一步说明 MeshSplats 如何与传统的网格渲染工具集成，其中使用 Nvdiffrast（Munkberg 等人，2022）渲染时效果最佳，因为它能高效处理具有不同透明度的多个组件。最后，我们展示了 MeshSplats 可以像 GS 一样进行微调。

高斯绘制（Gaussian Splatting）

高斯绘制（GS）技术通过一组三维高斯分布构建三维场景：

\[N(m, \Sigma), \sigma, c\]

每个元素的定义取决于其位置（均值）\(m\)、对应的协方差矩阵 \(\Sigma\)、透明度 \(\sigma\) 和颜色 \(c\)。颜色表示采用球谐函数（Spherical Harmonics, SH）方法（Fridovich-Keil 等人，2022；Müller 等人，2022）。然而，需要注意的是，用传统的 RGB 颜色替换 SH 是允许的，尽管这会导致重建质量略有下降，主要是因为它对视图方向不敏感。在 MeshSplats 中，我们使用传统的网格渲染器，因此需要使用 RGB 颜色。这种方法与传统的 GS 相比，渲染质量略有降低，但它有助于整合外部光照。

GS 算法通过顺序优化三维高斯参数来构建 NeRF 表示。这种技术由于依赖于投影高斯组件的渲染过程而非常高效。GS 优化方法涉及迭代渲染并将结果图像与数据集中的输入视图进行比较。然而，从三维到二维的投影可能会导致几何位置的错位。因此，GS 优化必须通过创建、移除或重新定位几何体来调整场景。准确的三维高斯协方差对于简洁的表示至关重要，因为较大的各向异性高斯可以高效覆盖广阔的均匀区域。

扁平高斯的 MeshSplats 转换

如上所述，在经典的 GS 模型中，每个元素由一组参数表征，包括一个协方差矩阵 \(\Sigma\)，该矩阵分解为：

\[\Sigma = RSS^TR^T \tag{1}\]

其中 \(R\) 是旋转矩阵，\(S\) 是包含缩放参数的对角矩阵。尽管有一些方法使用扁平高斯（Guedon & Lepetit，2024；Waczyńska 等人，2024；Huang 等人，2024），但我们使用 GaMeS 表示（Waczyńska 等人，2024）：

\[N(m, R, S) \tag{2}\]

图2. MeshSplats（我们的方法）将平面高斯转换为网格的过程，其中\(m\)是高斯的均值，\(r_2\)和\(r_3\)是旋转矩阵\(R\)的第二和第三列（见公式(1)），而\(sr_1\)和\(sr_2\)表示公式(3)中的缩放旋转1和缩放旋转2。

其中 \(m\) 是高斯的均值，\(S = \text{diag}(s_1, s_2, s_3)\)，且 \(s_1 = \varepsilon\)，\(R\) 是定义为 \(R = [r_1, r_2, r_3]\) 的旋转矩阵，其中 \(r_i \in \mathbb{R}^3\)。因此，高斯组件可以用网格面近似。我们的模型使用从椭圆内嵌的多边形构造的简单网格，如图2 所示。

扁平高斯转换为网格的过程通过三个超参数控制：缩放乘数 \(\text{scale_mul}\)、每个高斯的三角形数量 \(\text{no_triag}\) 和透明度乘数 \(\text{opac_mul}\)。每个高斯被表示为中心在其均值位置的网格，其形状和方向由其缩放和旋转参数决定。由于高斯被视为二维结构，因此忽略其缩放参数（\(s_i = \varepsilon\)，其中 \(s_i\) 很小）及其对应的旋转向量，从而将问题简化为二维。

首先，计算定义椭圆主轴和次轴的两个正交向量：

\[\text{scaled_rot1} = \text{scale_mul} \cdot \exp(s_2) \cdot r_2\] \[\text{scaled_rot2} = \text{scale_mul} \cdot \exp(s_3) \cdot r_3 \tag{3}\]

其中 \(r_2\) 和 \(r_3\) 分别是旋转矩阵 \(R\) 的第二列和第三列，且 \(\text{scale_mul} = 2.7\)。接下来，在椭圆边界上生成 \(\text{no_triag}\) 个点以构建网格。通过计算范围在 \([-\pi, \pi]\) 内的 \(\text{no_triag}\) 个均匀分布的角度 \(\theta_i\) 来完成此操作。对于每个角度 \(\theta_i\)，顶点 \(v_i\) 的计算公式如下：

\[v_i = m + \cos(\theta_i) \cdot \text{scaled_rot1} + \sin(\theta_i) \cdot \text{scaled_rot2} \tag{4}\]

然后，将网格构造为三角形扇形，其中所有三角形共享椭圆中心作为公共原点。每个三角形面由中心点和两个连续的边界顶点定义，每个高斯生成 \(\text{no_triag}\) 个三角形。这种结构将扁平高斯近似为一组相连的三角形。在所有实验中，我们使用 \(\text{no_triag} = 8\)。

在我们的方法中，为网格中的每个顶点分配颜色，所有顶点继承对应高斯的颜色。这确保了网格在最终渲染中视觉上表示高斯的颜色。高斯在训练时不使用球谐函数，以确保与网格渲染器的兼容性。另一方面，透明度也分配给网格中的每个顶点，所有顶点继承对应高斯的透明度。对于边界顶点，透明度通过 \(\text{opac_mul}\) 缩放，以在网格中创建透明度的线性插值。这近似了高斯透明度的衰减，其衰减速率由 \(\text{opac_mul}\) 参数控制。在所有实验中，\(\text{opac_mul} = 0.2\)。

值得注意的是，通过这一过程，每个扁平高斯被转换为一个网格，保留了其空间范围、方向和视觉属性。超参数 \(\text{scale_mul}\)、\(\text{no_triag}\) 和 \(\text{opac_mul}\) 提供了对结果三角形集合的保真度和外观的控制，从而实现了对空间高斯的灵活且准确的表示。

三维高斯的 MeshSplats 转换

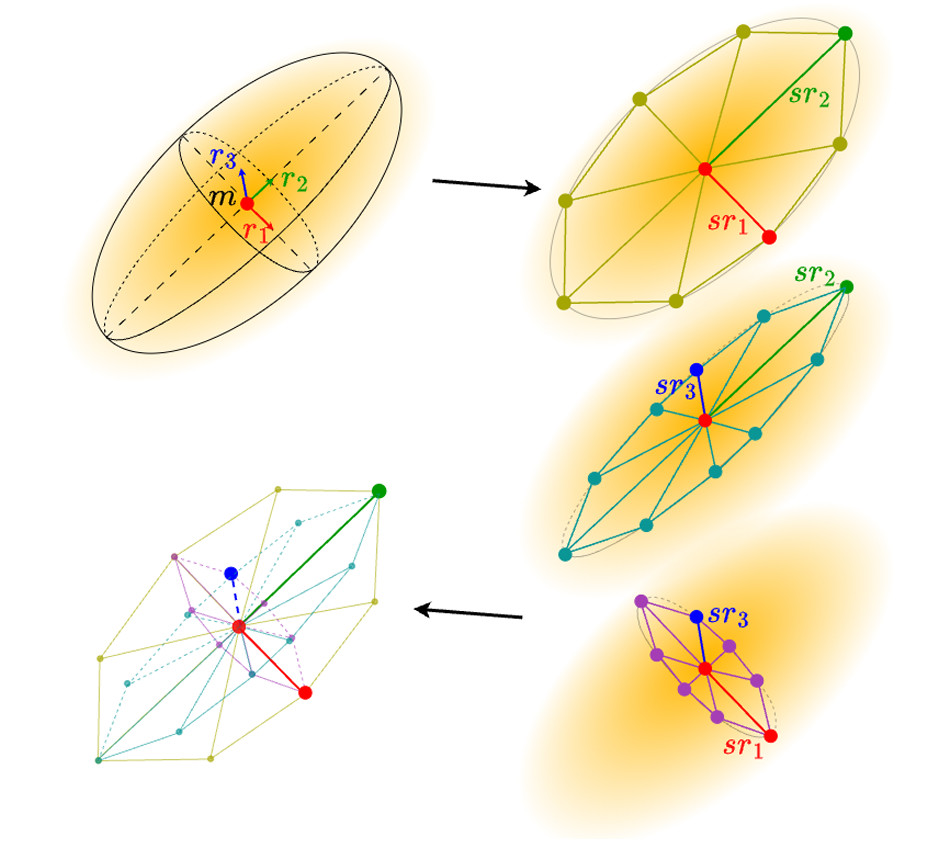
图4. MeshSplats（我们的方法）将3D高斯转换为网格的过程。这里\(m\)是高斯的均值，\(r_1\)、\(r_2\)和\(r_3\)是旋转矩阵\(R\)的列，\(sr_1\)、\(sr_2\)和\(sr_3\)表示公式(5)中的缩放旋转1、缩放旋转2和缩放旋转3。该转换类似于平面情况（见图2），但扩展到由向量对\((r_1,r_2)\)、\((r_1,r_3)\)和\((r_2,r_3)\)张成的三个表面。为每个表面创建网格，并合并为一个表示3D高斯的单一网格。

三维高斯转换为网格的过程是基于扁平高斯的方法扩展到三维空间。二维方法将高斯近似为扁平椭圆，而三维方法则将它们表示为椭球体，捕捉其完整的空间范围。这一过程由三个超参数控制：缩放乘数 \(\text{scale_mul}\)、每个高斯的三角形数量 \(\text{no_triag}\) 和透明度乘数 \(\text{opac_mul}\)，这些参数与二维情况下的值保持一致。然而，由于维度的增加，出现了几个显著的区别。因此，与二维情况中丢弃最小的缩放值及其对应的旋转向量不同，三维高斯保留了所有三个缩放常数和旋转向量。转换过程的图形总结如图4 所示。

首先，计算定义椭球体主轴的三个正交向量如下：

\[\begin{align*} \text{scaled_rot1} &= \text{scale_mul} \cdot \exp(s_1) \cdot r_1, \\ \text{scaled_rot2} &= \text{scale_mul} \cdot \exp(s_2) \cdot r_2, \\ \text{scaled_rot3} &= \text{scale_mul} \cdot \exp(s_3) \cdot r_3, \tag{5} \end{align*}\]

其中 \(r_1, r_2, r_3\) 分别是旋转矩阵 \(R\) 的列向量。这些向量定义了椭球体在三维空间中的方向和范围。接下来，在由向量对 \((\text{scaled_rot1}, \text{scaled_rot2})\)、\((\text{scaled_rot1}, \text{scaled_rot3})\) 和 \((\text{scaled_rot2}, \text{scaled_rot3})\) 定义的每个三维正交表面上生成 \(\text{no_triag}\) 个边界点。对于每个表面，计算范围在 \([-\pi, \pi]\) 内的 \(\text{no_triag}\) 个均匀分布的角度 \(\theta_i\)。然后，对于每个角度 \(\theta_i\)，顶点 \(v_i\) 的计算方式与二维方法类似，即：

\[v_i = m + \cos(\theta_i) \cdot \text{scaled_rota} + \sin(\theta_i) \cdot \text{scaled_rotb}, \tag{6}\]

其中 \(\text{scaled_rota}\) 和 \(\text{scaled_rotb}\) 是跨越当前表面的向量。表面交点处的点被共享，以避免冗余顶点并确保无缝的网格结构。

然后，网格被构造为一组三角形扇形，为每个表面分配一个扇形。每个三角形面的定义方式与二维方法类似，每个高斯生成 \(3 \cdot \text{no_triag}\) 个三角形。这种结构将三维高斯近似为一组分布在三个正交表面上的相连三角形。颜色和透明度以与二维解决方案相同的方式分配给网格中的每个顶点。

需要注意的是，这一过程将每个三维高斯转换为网格，与前面的情况非常相似。主要区别在于使用三个正交面来捕捉整个三维结构，以及在面之间共享顶点以保持网格效率。然而，这种表示方式比二维情况有更多的顶点和三角形，导致模型的内存使用量增加，渲染速度变慢。

在 Nvdiffrast 中渲染 MeshSplats

由 Nvdiffrast 在网格集合上进行的栅格化过程，涉及将三维顶点转换为二维屏幕空间，并最终将这些顶点渲染为图像。该过程首先使用模型-视图-投影（MVP）矩阵将顶点转换到裁剪空间，将其映射到标准化设备坐标。这一步确保了顶点在屏幕上渲染时的正确位置。

栅格化过程采用深度剥离技术来管理透明度和重叠几何体。这种方法通过迭代渲染场景的多个图层，确保每个图层正确地与其他图层合成。每个图层的栅格化输出及其导数被计算出来，以便精确地在三角形上插值顶点颜色。然后，插值后的颜色与前一层积累的颜色通过 alpha 通道考虑透明度进行混合。这种混合过程确保了透明区域在最终图像中被准确表示。

在处理完所有图层后，从累积的颜色缓冲区中提取最终的 RGB 和 alpha 值。RGB 值表示渲染的图像，而 alpha 通道捕获透明度。这种方法利用了 Nvdiffrast 的效率和灵活性来渲染复杂对象，特别适合于具有详细几何结构和透明度的场景。深度剥离确保了重叠元素的正确处理，从而产生高质量的渲染效果。

MeshSplats 的微调

我们的微调流程接受由高斯（二维或三维）创建的网格集合作为输入，并对其进行优化以更好地匹配目标场景。该流程包括几个阶段：顶点变换、栅格化、混合、损失计算，随后是迭代优化和剪枝。在以下描述中，我们对流程中的每个步骤进行了详细的概述。

顶点变换：如前所述，输入的网格集合顶点使用 MVP 矩阵进行变换。该矩阵将三维顶点投影到二维图像空间以进行栅格化。每个顶点 \(v_i\) 的变换如下：

\[v_{\text{transformed}}^i = \text{MVP} \cdot v_i. \tag{7}\]

栅格化和混合：栅格化和混合过程遵循上述方法，采用深度剥离技术管理具有不同透明度的重叠网格。通过整合多个栅格化图层，输出图像得以生成，从而确保每个网格元素的贡献得以保留。

损失函数：用于优化的损失函数是 L1 损失和结构相似性指数（SSIM）的加权组合。这种方法与三维高斯绘制中使用的方法类似。因此，损失函数定义如下：

\[L = \lambda \cdot L1(\hat{y}, y) + (1 - \lambda) \cdot \text{SSIM}(\hat{y}, y), \tag{8}\]

其中 \(y\) 是真实图像，\(\hat{y}\) 是预测图像，\(\lambda = 0.6\) 是平衡常数。

优化和剪枝：优化过程通过更新网格集合的顶点来最小化公式 (8) 中的损失函数。具体来说，顶点的颜色和透明度以学习率 \(lr_{\text{color}}\) 进行优化。顶点的位置也进行了优化，但学习率较弱，为 \(lr_{\text{verts}} = \exp(-3) \cdot lr_{\text{color}}\)，以确保位置更新是微妙且稳定的。

每 10 个周期进行一次剪枝步骤，移除冗余的面和顶点。如果一个面的所有顶点的透明度都低于 \(\exp(-4)\) 的阈值，则该面会被剪枝。此外，如果其他面没有使用被剪枝面的顶点，则这些顶点也会被删除。这一剪枝步骤有助于减少内存使用量和计算复杂度，同时保持场景表示的保真度。

4 实验

在本节中，我们展示了我们的实验研究结果，包括定量和定性结果。为了阐明 MeshSplats 在不同高斯绘制（GS）初始化下的功能，我们进行了相应的消融研究。此外，我们还探讨了算法在参数化和训练后的表现。源代码以及额外的实验结果可在 https://github.com/gwilczynski95/meshsplats 获取。

数据集和评估指标

提出的 MeshSplats 框架在三个标准数据集上进行了评估：MipNeRF360（Barron 等人，2022）、Tanks and Temples（Knapitsch 等人，2017）和 Deep Blending（Hedman 等人，2018）。为了确保一致性，我们考察了与 Moenne-Loccoz 等人（2024）相同的场景。具体来说，对于 Mip-NeRF360，我们分析了四个室内场景（房间、柜台、厨房和盆栽）和三个室外场景（自行车、花园和树桩）。对于 Tanks and Temples 数据集，我们重点关注两个大型室外场景（火车和卡车）。此外，对于 Deep Blending 数据集，我们包含了两个室内场景（游戏室和 drjohnson）。按照先前的研究，室内场景的图像按 2 倍因子下采样，室外场景按 4 倍因子下采样进行评估。所有数据集均采用统一的训练/测试分割。

在评估过程中，使用了三个标准指标：PSNR、SSIM（Wang 等人，2004）和 LPIPS（Zhang 等人，2018）。

定量结果

MeshSplats 的性能在上述三个基准数据集上进行了评估，定量结果总结于表 1。在 Mip-NeRF360 和 Tanks and Temples 数据集上，结果与现有方法相当，SSIM、PSNR 和 LPIPS 指标与 3DGS（Kerbl 等人，2023）和 RaySplats（Byrski 等人，2025）等最新方法非常接近。例如，在 Mip-NeRF360 数据集上，尽管采用基于网格的表示，我们的方法仍达到了与基于栅格化的技术相当的分数。同样，在 Tanks and Temples 数据集上，性能指标保持竞争力，反映了在室外场景重建中的稳健性。值得注意的是，MeshSplats 在 Deep Blending 数据集上表现出色。这一结果表明，我们的方法在处理复杂的室内几何结构和透明效果方面非常有效，因为它超越了几种基线方法，并接近 3DGS 等领先模型的性能指标。

定性结果

图5. 不同类型的渲染示例：第一列显示地面真实图像，第二列显示使用Nvdiffrast优化的MeshSplats（我们的方法）的渲染，第三列显示将球谐函数设置为零的3D高斯泼溅的渲染。前两行包含来自Mip-NeRF360数据集的数据，其中MeshSplats和3DGS的分辨率参数设置为4。最后一行是来自Tanks and Templates数据集的卡车示例，其中MeshSplat和3DGS的分辨率参数设置为1。

观察发现，使用 Nvdiffrast 渲染的 MeshSplats 在视觉质量上几乎与没有球谐函数的 3DGS 相同，如图5 所示。两种方法在建模透明表面上的反射时表现出类似的局限性，例如在玻璃上，光的相互作用的近似导致了伪影。在高频区域，如密集的草丛中，MeshSplats 提供了略微粗糙的重建，细节有所减少。尽管存在这些小的差异，但我们的模型的整体保真度与 3DGS 产生的结果相当，从而突显了其在基于网格的框架内复制基于高斯的渲染优势的能力。

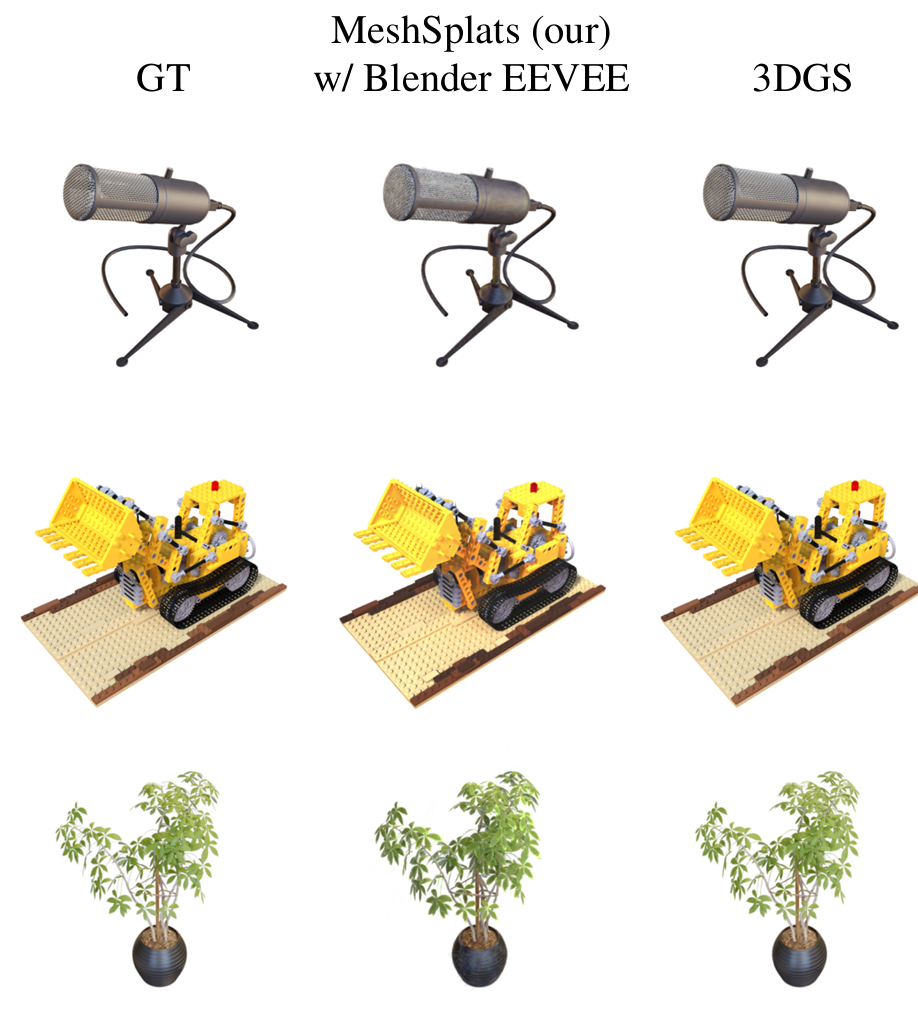
图6. 不同类型的渲染示例：第一列显示地面真实图像，第二列显示使用Blender的EEVEE渲染器优化的MeshSplats（我们的方法）的渲染，其中材料配置为HASHEDblend方法并禁用背面剔除，第三列显示将球谐函数设置为零的3D高斯泼溅的渲染。所有图像均来自NeRF Synthetic数据集。地面真实图像和Blender渲染之间的颜色差异是由于不同的照明条件造成的。

此外，当使用 Blender 的 EEVEE 引擎渲染时，MeshSplats 也产生了与 3DGS 相当的视觉上合理的渲染结果，如图6 所示。然而，在需要复杂几何精度的区域，例如 ficus 场景的细小叶结构，高频细节部分丢失。尽管如此，大多数场景仍保持了逼真的质量，具有连贯的几何结构和准确的颜色表示。观察到一些小的伪影，这些伪影归因于基于网格的高斯透明度衰减的近似，但它们并没有显著影响整体视觉完整性。这些结果证实了我们的方法对传统渲染管线的适应性，同时保持了竞争性的渲染质量。

消融研究

MeshSplats 可以与经典的高斯绘制一起使用，但它专门用于建模扁平高斯场景。因此，我们进行了消融研究，将我们的方法与三种 GS 初始化变体进行比较：3DGS（Kerbl 等人，2023）、2DGS（Huang 等人，2024）和 GaMeS（Waczyńska 等人，2024）。所有方法都训练生成使用 RGB 颜色表示的 splats，省略球谐函数以确保与网格渲染的兼容性。训练后，将得到的高斯组件转换为未优化的网格集合。对于扁平高斯（2DGS 和 GaMeS），通过将每个高斯近似为具有八个三角形（\(\text{no_triag} = 8\)）的多边形，并使用 2.7 的缩放乘数（\(\text{scale_mul} = 2.7\)）来构建网格。对于 3DGS，该过程扩展到三个正交表面，生成三维网格表示。随后，使用 Nvdiffrast 渲染器对 MeshSplats 进行优化，该渲染器促进了带有深度剥离的可微分栅格化和混合。优化流程采用了结合 L1 和 SSIM 的损失函数，顶点位置和颜色在 15 个周期内迭代更新。

消融研究的结果如表 2 所示。当使用 3DGS 初始化时，由于将三维高斯拟合到网格结构的固有复杂性，所有数据集上都观察到了适度的性能下降。对于 GaMeS，在 Mip-NeRF360 和 Deep Blending 上表现与 RGB 对应方法相当，表明尽管进行了转换，但有效地保留了几何保真度。另一方面，当使用 2DGS 初始化时，MeshSplats 在 Deep Blending 上实现了更高的 PSNR 和更低的 LPIPS，表明在复杂的室内场景中重建质量有所提高。尽管在室外数据集上观察到了轻微的性能下降，但结果突显了我们的模型在需要精细细节处理的场景中匹配或超越其初始化方法的能力，尽管其采用了独特的基于网格的范式。

图7. 使用Nvdiffrast渲染的同一场景在优化前（左）和优化后（右）的比较。未优化的MeshSplats渲染缺乏精细的结构细节，如红色椭圆标记的缺失或定义不清的自行车辐条。场景中出现了大量浮动物体，影响了整体一致性。相比之下，优化的MeshSplats结果显示出显著的改进，浮动物体完全消失，辐条或草等细节清晰重建。它还表现出更高的几何精度和视觉清晰度，表面更平滑，自行车框架及其周围元素的纹理表现更丰富。

图8. 使用Blender的EEVEE渲染器渲染的同一场景在优化前（左）和优化后（右）的比较。虽然我们的未优化模型展示了潜力，但在细节上存在不足，特别是挖掘机平台边缘，如红色椭圆所示。值得注意的是，优化的MeshSplats（我们的方法）渲染并未出现这些问题。

此外，还全面评估了优化过程对 MeshSplats 的影响。如图7 所示，未优化的模型在整个场景中散布了大量的浮动物体（即多余的几何伪影）。此外，高频细节（如自行车辐条和密集草丛）未能得到充分解析或完全缺失，导致几何精度降低。在优化过程中，这些限制得到了相当程度的解决。具体来说，移除了浮动物体，并以更高的清晰度重建了细小的结构元素（如辐条和草叶）。同样，在图8 中，也突出了未优化网格在锐利边缘保持方面的挑战，用红色椭圆标记。经过优化过程后，边缘锐度和几何连贯性得到了显著提升，从而更准确地呈现了复杂几何结构。

总之，消融研究的结果突显了优化流程在增强初始网格转换过程中的重要性。尽管未优化的 MeshSplats 提供了一个合理的起点，但优化阶段对于减少伪影、提高细节保留以及与最新渲染技术达到一致至关重要。

5 结论

在本文中，我们介绍了 MeshSplats，这是一种通过将高斯绘制（Gaussian Splatting, GS）转换为类似网格的结构来有效克服其缺点的方法，从而使其能够与光线追踪技术集成。这种转换利用了光线追踪的优势，例如改进的光照、阴影和反射，从而提升了渲染质量。我们的方法提供了一种即时、实用的解决方案，并通过 MeshSplats 优化算法进一步提升渲染效果。广泛的实验研究验证了我们技术的有效性和适应性，证明了其在多样化数据集上的广泛适用性。值得注意的是，尽管 MeshSplats 采用了独特的基于网格的表示方法，但它已经展示了渲染逼真场景的能力，其视觉质量与高斯绘制技术相当，甚至在某些情况下超越了后者。优化后的浮动物体消除和结构细节的精细化进一步凸显了其在平衡几何精度与渲染保真度方面的优势。这些特性强化了我们方法作为一种高质量渲染的稳健替代方案的潜力，适用于计算机图形学和图像处理领域。

局限性

我们方法的两个关键局限性已被识别。首先，在建模大面积、低纹理区域时（例如，Tanks and Temples 数据集中的 Train 场景中的纯色天空），会出现伪影，如几何碎片和透明度不一致。这一问题源于基于网格的透明度插值，它难以在均匀区域重现高斯元素的平滑衰减特性。值得注意的是，这一问题在 DeepBlending 的室内场景（如墙面）中并未出现。其次，使用 3DGS 初始化会产生密集的网格划分，导致顶点数量过多，从而增加内存使用量并降低渲染效率。尽管使用扁平高斯（例如 2DGS、GaMeS）可以缓解这一问题，但 3DGS 生成的网格对于实时应用仍然具有较高的计算负担。