如果有研究透明物体场景研究的研究者，可以通过邮箱zhangwenniu@163.com联系我，我目前创建了一个透明物体场景研究的研究者交流群，欢迎感兴趣的研究者加入。

论文链接

• TOG Link

发表时间：29 July 2007

发表于ACM Transactions on Graphics (TOG)

重点难点讲解

这篇论文《Eikonal Rendering: Efficient Light Transport in Refractive Objects》提出了一种基于几何光学的实时渲染方法，用于高效地渲染复杂折射物体中的多种光照效果。以下是对论文的重点和难点的讲解：

论文重点

1. 实时渲染复杂折射物体的光照效果

   论文的核心目标是实现实时渲染具有复杂光学特性的折射物体，例如具有任意变化的折射率、非均匀衰减、各向异性散射和反射属性的物体。这些效果在传统方法中很难实时实现。

2. 基于Eikonal方程的光照传输模型

   论文提出了一种基于Eikonal方程的光照传输框架，能够快速计算弯曲光线的传播路径。这种方法结合了粒子追踪的效率和几何光学的理论基础，适用于复杂折射场景。

3. 自适应波前追踪技术

   为了高效地计算光强分布，论文采用自适应波前追踪技术。通过在三维体积中传播波前，并动态调整采样密度，可以避免欠采样问题，同时减少计算量。

4. GPU加速实现

   论文详细描述了如何将算法映射到GPU上实现。通过利用GPU的并行计算能力，论文实现了复杂折射物体的实时渲染，包括动态光源更新和多物体渲染。

5. 多种光学效果的统一处理

   论文的框架能够同时处理多种光学效果，如折射、反射、各向异性散射、发射和吸收等。这种统一的处理方式使得渲染结果更加真实。

6. 实验结果与性能分析

   论文展示了多个复杂场景的渲染结果，并分析了算法的性能。在800×600分辨率下，单个物体的渲染帧率可达25fps，显示了算法的实时性。

论文难点

1. Eikonal方程的物理理解与数学推导

   Eikonal方程是几何光学的核心方程，用于描述光波前的传播。论文中对方程的推导和参数化（如常空间步长和常时间步长的参数化）需要较强的物理和数学基础。理解这些推导对于掌握算法的核心思想至关重要。

2. 自适应波前追踪的实现细节

   自适应波前追踪是论文的关键技术之一，但其实现细节较为复杂。例如，如何动态调整波前的采样密度、如何处理波前的分裂和终止，以及如何在GPU上高效实现这些操作，都是需要深入理解的部分。

3. GPU上的数据结构与算法优化

   论文提出了一系列针对GPU的优化方法，如使用HistoPyramid进行数据压缩和扩展。这些方法的实现需要对GPU架构和编程模型有深入了解。此外，如何在预Shader Model 4.0的硬件上实现这些功能也是一个挑战。

4. 处理复杂折射物体的光学特性

   论文需要处理折射率变化、各向异性散射等复杂的光学特性。这些特性在数学建模和实际实现中都较为复杂，尤其是在实时渲染的约束下。

5. 光源更新与动态场景的处理

   当光源位置发生变化时，需要重新计算光照分布。论文虽然实现了较快的更新时间（5-10秒），但如何进一步优化这一过程以适应更动态的场景是一个潜在的难点。

6. 平衡精度与实时性

   论文在实现实时渲染的同时，需要在精度和性能之间做出权衡。例如，对折射率场的平滑处理可能会引入一些视觉误差，但这是为了实现高效的计算。

总结

这篇论文的核心贡献在于提出了一种基于Eikonal方程的高效渲染框架，能够实时渲染复杂折射物体的多种光学效果。其难点主要集中在对几何光学理论的理解、自适应波前追踪技术的实现，以及GPU上的优化。通过这些技术，论文在实时性和视觉效果之间取得了良好的平衡，为复杂折射物体的渲染提供了新的思路。

论文详细讲解

这篇论文《Eikonal Rendering: Efficient Light Transport in Refractive Objects》提出了一种基于几何光学（Geometric Optics）的实时渲染方法，用于高效地渲染复杂折射物体中的多种光照效果。以下是对这篇论文的详细讲解，涵盖其背景、方法、实现和结果。

1. 论文背景

在计算机图形学中，渲染复杂折射物体（如水晶玻璃、宝石、烟雾中的物体等）是一个极具挑战性的问题。这些物体的视觉效果来源于复杂的光与物质相互作用，包括：

• 折射和反射：光线在物体表面发生反射和折射，折射率可能在空间中变化。

• 各向异性散射：物体内部的光线可能以特定方向散射。

• 非均匀吸收：光线在物体内部传播时可能因吸收而衰减。

• 体积焦散（Volume Caustics）：光线聚焦形成的复杂光斑。

这些效果在传统渲染方法中很难实时实现，因为它们涉及复杂的光线路径和非线性传播。以往的方法通常需要离线计算或仅支持简单场景。本文的目标是提出一种能够在普通图形硬件上实时渲染这些复杂效果的方法。

2. 核心贡献

论文的主要贡献包括：

1. 基于Eikonal方程的光照传输框架：提出了一种基于几何光学的数学框架，能够快速计算复杂折射物体中的光线传播路径。

2. 自适应波前追踪技术：通过自适应地追踪光波前，高效地计算场景中的光照分布。

3. GPU加速实现：将算法映射到GPU上，实现了复杂折射物体的实时渲染。

4. 统一处理多种光学效果：在同一个框架内处理折射、反射、各向异性散射、吸收和发射等效果。

3. 方法详解

3.1 基于Eikonal方程的图像生成模型

论文的核心是基于几何光学的Eikonal方程：

\[|▽S| = n\]

其中，$ S $ 是光程函数，$ n $ 是折射率。基于Eikonal方程，论文推导出光线的运动方程：

\[\frac{d}{ds}\left(n \frac{dx}{ds}\right) = ▽n\]

这个方程描述了光线在非均匀折射率场中的传播路径。

论文进一步将光线传播问题转化为一组常微分方程（ODE），并利用GPU进行快速求解。这种方法允许光线在物体内部和表面自然地弯曲，同时支持全反射（Total Internal Reflection）。

3.2 自适应波前追踪

为了高效地计算场景中的光照分布，论文提出了一种自适应波前追踪技术。波前是光程函数的等值面，光线总是垂直于波前传播。论文通过以下步骤实现波前追踪：

1. 波前初始化：根据光源类型（如点光源或方向光源），初始化波前。

2. 波前传播：使用微分方程更新波前的位置和方向。

3. 光照强度计算：基于几何光学的强度定律，计算每个波前片段的光照强度。

4. 自适应细分：当波前片段过大时，自动细分以避免欠采样。

5. 波前终止：当波前能量过低或离开场景范围时，停止追踪。

这种方法能够在复杂折射场景中高效地计算光照分布，同时避免了传统方法中的采样问题。

3.3 GPU加速实现

论文详细描述了如何将上述方法映射到GPU上实现：

1. 数据存储：场景的折射率、吸收率、散射参数等存储在3D纹理中。

2. 波前追踪：使用GPU的并行计算能力，将波前表示为一组粒子，每个粒子代表波前的一个片段。

3. 光照计算：通过粒子追踪，计算每个体素的光照方向和强度，并存储在3D纹理中。

4. 视图渲染：基于预计算的光照分布，使用弯曲的视线（View Rays）进行快速体绘制。

论文还提出了一些优化方法，如使用HistoPyramid进行数据压缩和扩展，以提高GPU上的效率。

4. 实验结果

论文展示了多个复杂场景的渲染结果，验证了方法的有效性：

1. 玻璃酒杯：渲染了装有红酒的玻璃酒杯，展示了复杂的折射、反射和焦散效果。

2. 琥珀色兔子：在烟雾环境中渲染了一个带有黑色嵌入物的琥珀色兔子，展示了各向异性散射和体积焦散。

3. 多物体场景：同时渲染了多个折射物体，并动态更新环境映射，展示了物体之间的相互折射效果。

在性能方面，论文在800×600分辨率下实现了25fps的渲染帧率。当光源位置发生变化时，光照分布的更新时间约为5-10秒。这些结果表明，该方法能够在普通图形硬件上实现实时渲染。

5. 论文的优缺点

优点

1. 统一框架：在一个框架内处理多种复杂光学效果，包括折射、反射、散射和焦散。

2. 实时性：能够在普通GPU上实现实时渲染，适合交互式应用。

3. 高效性：通过自适应波前追踪和GPU优化，显著提高了计算效率。

4. 物理合理性：基于几何光学的理论基础，结果具有较高的物理合理性。

缺点

1. 场景限制：由于基于体积表示，场景大小受限于显存容量。

2. 精度问题：为了提高效率，对折射率场进行了平滑处理，可能导致一些精度损失。

3. 动态场景支持有限：虽然光源位置可以动态更新，但对于更复杂的动态场景（如物体运动）支持有限。

6. 总结

这篇论文提出了一种基于几何光学的实时渲染方法，能够高效地渲染复杂折射物体中的多种光学效果。通过自适应波前追踪和GPU加速，该方法在普通图形硬件上实现了实时渲染，并在多个复杂场景中展示了其有效性。这种方法为复杂光学效果的实时渲染提供了一种新的思路，具有重要的应用价值。

论文方法部分详解

方法概述

论文的核心目标是实现实时渲染复杂折射物体的多种光学效果，包括折射、反射、各向异性散射、焦散等。为此，作者提出了一种基于几何光学的光照传输框架，该框架基于Eikonal方程，通过自适应波前追踪技术高效地计算场景中的光照分布，并利用GPU加速实现。以下是方法部分的详细讲解：

1. 基于Eikonal方程的光照传输框架

1.1 Eikonal方程与光线传播

Eikonal方程是几何光学的核心方程，用于描述光波前的传播： \(|▽S| = n\)

其中：

• $ S $ 是光程函数，表示光从光源到达某点的最小传播时间。

• $ n $ 是折射率，可能在空间中变化。

基于Eikonal方程，论文推导出光线的运动方程：

\[\frac{d}{ds}\left(n \frac{dx}{ds}\right) = ▽n\]

这个方程描述了光线在非均匀折射率场中的传播路径。它允许光线在物体内部和表面自然地弯曲，并支持全反射。

1.2 简化图像生成模型

为了实现实时渲染，论文对复杂的图像生成模型进行了简化，假设：

1. 场景中的光来自离散的光源。

2. 每个点只接收来自每个光源的有限数量的光线。

基于这些假设，论文将积分方程转化为离散求和形式，从而能够高效地计算每个点的光照贡献。

1.3 光线传播的数学表示

论文将光线传播问题转化为一组常微分方程（ODE），具体如下：

1. 位置更新：

   \[\frac{dx}{ds} = \frac{v}{n}\]

2. 方向更新：

   \[\frac{dv}{ds} = ▽n\]

其中：

• $ x $ 是光线的位置。

• $ v $ 是光线的方向。

• $ n $ 是折射率。

• $ s $ 是沿光线的参数。

这些方程可以通过数值积分方法（如欧拉法或龙格-库塔法）求解，从而实现光线的传播。

2. 自适应波前追踪技术

2.1 波前的定义与传播

波前是光程函数 $ S $ 的等值面，光线总是垂直于波前传播。论文通过以下步骤实现波前追踪：

1. 波前初始化：根据光源类型（如点光源或方向光源），初始化波前。波前被离散化为一组粒子，每个粒子表示波前的一个片段。

2. 波前传播：使用上述ODE更新波前的位置和方向。每个粒子的运动遵循光线传播方程。

3. 光照强度计算：基于几何光学的强度定律，计算每个波前片段的光照强度。具体公式为：

   \[\Delta E_\omega(t) = \Delta E_\omega(0) \frac{A(0)}{A(t)} e^{-\int_0^t \sigma(c(\hat{t})) \, d\hat{t}}\]

   其中：

   • $ \Delta E_\omega $ 是光照强度。

   • $ A(t) $ 是波前片段的面积。

   • $ \sigma $ 是吸收系数。

2.2 自适应细分与终止

为了确保波前的采样密度足够高，论文采用了自适应细分策略：

1. 自适应细分：当波前片段的面积超过一个体素时，自动将其细分为更小的片段。这避免了欠采样问题。

2. 波前终止：当波前片段的能量过低或离开场景范围时，停止追踪该片段。此外，论文还检测波前的奇异性（如全反射点），并丢弃穿过奇异点的片段。

2.3 波前的存储与更新

波前被存储为一组粒子，每个粒子包含位置、方向和光照强度信息。在每一步中，波前的更新包括：

1. 位置和方向更新：根据ODE更新每个粒子的位置和方向。

2. 光照强度更新：根据强度定律更新每个粒子的光照强度。

3. 波前细分与终止：根据上述策略动态调整波前的采样密度。

3. GPU加速实现

3.1 数据存储

输入场景被存储为一组3D纹理，包括：

1. 折射率场及其梯度场。

2. 吸收率场。

3. 散射参数和BRDF参数。

4. 物体边界指示器（用于表示物体表面）。

这些纹理被用于快速访问场景中的光学属性。

3.2 波前追踪的GPU实现

波前追踪过程被映射到GPU上，具体步骤如下：

1. 波前初始化：在GPU上初始化波前粒子，根据光源类型生成平面或球面波前。

2. 波前传播：使用GPU的并行计算能力，同时更新所有波前粒子的位置和方向。

3. 光照强度计算：在GPU上计算每个波前片段的光照强度，并将其存储在3D纹理中。

4. 波前细分与终止：通过GPU实现波前的自适应细分和终止操作。

论文还提出了一种基于HistoPyramid的数据压缩和扩展算法，用于高效地处理波前的动态变化。

3.3 视图渲染

在光照分布预计算完成后，论文使用一种快速光线投射方法渲染用户视图：

1. 光线投射：根据预计算的光照分布，使用弯曲的视线（View Rays）进行体绘制。

2. 光照计算：在每个体素处，根据预计算的光照方向和强度，计算最终的光照效果。

3. 环境映射：使用动态环境映射技术近似背景光照。

所有计算均在GPU上完成，确保了实时渲染的效率。

4. 方法总结

论文提出的方法基于几何光学的Eikonal方程，通过自适应波前追踪技术高效地计算复杂折射物体中的光照分布，并利用GPU加速实现。这种方法的核心优势在于：

1. 统一框架：在一个框架内处理多种复杂的光学效果。

2. 高效性：通过自适应波前追踪和GPU加速，显著提高了计算效率。

3. 实时性：能够在普通图形硬件上实现实时渲染。

然而，这种方法也有一定的局限性，例如场景大小受限于显存容量，且对折射率场的平滑处理可能导致精度损失。

重点内容讲解

欧拉法（Euler’s Method）和龙格-库塔法（Runge-Kutta Methods）

欧拉法（Euler’s Method）和龙格-库塔法（Runge-Kutta Methods）是两种常用的数值积分方法，用于求解常微分方程（ODE）的初值问题。以下是对这两种方法的详细讲解：

1. 欧拉法（Euler’s Method）

1.1 基本思想

欧拉法是最简单的数值积分方法，它基于泰勒展开式的前两项来近似解。对于一个初值问题：

\[y' = f(x, y), \quad y(x_0) = y_0\]

欧拉法的迭代公式为：

\[y_{n+1} = y_n + h f(x_n, y_n)\]

其中：

• $ h $ 是步长，即每次迭代的 $ x $ 值的增量。
• $ (x_n, y_n) $ 是当前点的坐标。
• $ f(x_n, y_n) $ 是当前点的斜率。

1.2 误差分析

欧拉法的局部截断误差为 $ O(h^2) $，即每一步的误差与步长的平方成正比。因此，为了提高精度，需要减小步长，但这会增加计算量。

2. 龙格-库塔法（Runge-Kutta Methods）

2.1 基本思想

龙格-库塔法是一类更精确的数值积分方法，它通过在每一步中计算多个中间点的斜率，来提高近似的精度。最常用的龙格-库塔法是四阶龙格-库塔法（RK4），其迭代公式为：

\[y_{n+1} = y_n + \frac{h}{6} (k_1 + 2k_2 + 2k_3 + k_4)\]

其中：

• $ k_1 = f(x_n, y_n) $
• $ k_2 = f(x_n + \frac{h}{2}, y_n + \frac{h}{2} k_1) $
• $ k_3 = f(x_n + \frac{h}{2}, y_n + \frac{h}{2} k_2) $
• $ k_4 = f(x_n + h, y_n + h k_3) $

2.2 误差分析

四阶龙格-库塔法的局部截断误差为 $ O(h^5) $，即每一步的误差与步长的五次方成正比。因此，与欧拉法相比，龙格-库塔法在相同的步长下具有更高的精度。

3. 比较与应用

3.1 精度与计算量

• 欧拉法：简单易实现，但精度较低，适用于对精度要求不高的场合。
• 龙格-库塔法：精度高，但计算量较大，适用于对精度要求较高的场合。

3.2 稳定性

• 欧拉法：稳定性较差，对于某些问题可能需要非常小的步长。
• 龙格-库塔法：稳定性较好，对于相同的问题，可以使用较大的步长。

3.3 应用示例

在论文《Eikonal Rendering: Efficient Light Transport in Refractive Objects》中，作者使用了欧拉法或龙格-库塔法来求解光线传播的常微分方程。具体选择哪种方法取决于对精度和计算量的权衡。在实际应用中，可以根据问题的具体需求来选择合适的数值积分方法。

波前（Wavefront）

在论文《Eikonal Rendering: Efficient Light Transport in Refractive Objects》中，波前（Wavefront） 是一个关键概念，用于描述光在复杂介质中传播的几何特性。它在自适应波前追踪技术中扮演了核心角色，用于高效地计算场景中的光照分布。以下是对波前的详细讲解，包括其物理意义、数学表示以及在论文中的具体应用。

1. 波前的物理意义

在几何光学中，波前 是一个光程函数 $ S(x, y, z) $ 的等值面，表示光从光源出发后，在某一时刻到达的空间点的集合。换句话说，波前是光传播的“前锋面”，它描述了光在介质中传播的几何路径。

• 物理特性：
  • 波前总是垂直于光线的传播方向。
  • 光线在波前上的传播速度取决于介质的折射率 $ n $。
  • 波前的形状会因介质的折射率变化而发生弯曲，例如在非均匀介质中，波前可能会聚焦或发散。
• 常见例子：
  • 平面波前：在均匀介质中，从无穷远处的光源发出的光形成平面波前。
  • 球面波前：从点光源发出的光形成球面波前。
  • 复杂波前：在非均匀介质（如折射物体内部）中，波前形状会变得复杂，可能形成焦散（Caustics）。

2. 波前的数学表示

波前的数学描述基于Eikonal方程： \(|▽S| = n(x, y, z)\)

其中：

• $ S $ 是光程函数，表示光从光源到达某点的最小传播时间。
• $ n $ 是介质的折射率，可能在空间中变化。

波前是光程函数 $ S $ 的等值面，即：

\[S(x, y, z) = \text{常数}\]

在论文中，波前被离散化为一组粒子（或称为波前片段），每个粒子携带以下信息：

• 位置 $ \mathbf{x} $：粒子在空间中的坐标。
• 方向 $ \mathbf{v} $：粒子的传播方向，即光线的方向。
• 光照强度 $ E $：粒子携带的光照能量。

3. 波前追踪技术

波前追踪是论文中用于高效计算光照分布的核心技术。它通过动态传播波前粒子，模拟光在复杂介质中的传播过程。以下是波前追踪的主要步骤：

3.1 波前初始化

根据光源类型初始化波前：

• 点光源：生成一个球面波前，粒子均匀分布在球面上。
• 方向光源：生成一个平面波前，粒子均匀分布在平面上。

3.2 波前传播

根据Eikonal方程，波前的传播可以表示为一组常微分方程（ODE）：

\(\frac{d\mathbf{x}}{ds} = \frac{\mathbf{v}}{n}\) \(\frac{d\mathbf{v}}{ds} = ▽n\)

其中：

• $ s $ 是沿光线的参数。
• $ n $ 是折射率。
• $ \mathbf{v} $ 是光线的方向。

这些方程可以通过数值积分方法（如欧拉法或龙格-库塔法）求解，从而更新波前粒子的位置和方向。

3.3 光照强度计算

根据几何光学的强度定律，波前片段的光照强度 $ E $ 在传播过程中会因折射率变化而衰减。具体公式为：

\[E(t) = E(0) \cdot \frac{A(0)}{A(t)} \cdot e^{-\int_0^t \sigma(\mathbf{x}(s)) \, ds}\]

其中：

• $ A(t) $ 是波前片段在时间 $ t $ 的面积。
• $ \sigma $ 是吸收系数，描述光在介质中的衰减。

3.4 自适应细分

为了确保波前的采样密度足够高，论文采用了自适应细分策略：

• 当波前片段的面积超过一个体素时，自动将其细分为更小的片段。这避免了欠采样问题，确保了光照分布的准确性。

3.5 波前终止

为了提高效率，论文在以下情况下终止波前片段的传播：

• 能量过低：当波前片段携带的光照强度低于某个阈值时，停止追踪。
• 离开场景范围：当波前片段离开预定义的体积范围时，停止追踪。
• 遇到奇异性：当波前片段穿过全反射点或其他奇异性时，停止追踪。

4. 波前在论文中的应用

在论文《Eikonal Rendering: Efficient Light Transport in Refractive Objects》中，波前追踪技术用于预计算场景中的光照分布。具体步骤如下：

1. 波前初始化：根据光源类型生成初始波前。
2. 波前传播与更新：通过数值积分方法动态传播波前，计算每个体素的光照方向和强度。
3. 光照分布存储：将计算得到的光照方向和强度存储在3D纹理中，用于后续的视图渲染。
4. 视图渲染：在渲染阶段，使用预计算的光照分布快速计算每个像素的光照效果。

通过波前追踪技术，论文能够在复杂折射物体中高效地模拟多种光学效果，如焦散、各向异性散射和体积光效。

5. 波前追踪的优势

• 高效性：通过自适应细分和动态传播，波前追踪能够在复杂场景中高效地计算光照分布。
• 物理合理性：基于几何光学的理论基础，波前追踪能够自然地处理折射、反射和全反射等现象。
• 灵活性：波前追踪可以处理任意形状的光源和复杂介质，适用于多种光学场景。

偏振光与非偏振光

非偏振光与偏振光的区别

1. 基本概念

• 非偏振光（Unpolarized Light）：
  • 非偏振光是指光波的振动方向在各个方向上随机分布的光。自然光源（如太阳光）通常是非偏振光，因为其光波的电场振动方向在所有方向上都是均匀分布的。
  • 非偏振光的特性可以用斯托克斯参数（Stokes parameters）描述，但通常在简化模型中不考虑偏振效应。
• 偏振光（Polarized Light）：
  • 偏振光是指光波的振动方向在某个特定方向上有序排列的光。偏振光可以通过特定的光学元件（如偏振片）或物理过程（如反射、折射）产生。
  • 偏振光的振动方向可以是线偏振（振动方向固定）、圆偏振（振动方向旋转）或椭圆偏振（振动方向椭圆轨迹）。

2. 物理特性

• 非偏振光：
  • 由于振动方向随机，非偏振光在通过光学元件时不会表现出偏振相关的特性。
  • 在反射和折射过程中，非偏振光的反射和透射遵循斯涅尔定律（Snell’s Law），但不会产生偏振效应。
• 偏振光：
  • 偏振光在通过光学元件（如偏振片、反射面）时会表现出特定的偏振效应。例如，反射光可能部分偏振，而透射光可能完全偏振。
  • 偏振光的反射和透射特性可以用菲涅尔方程（Fresnel Equations）描述，这些方程考虑了偏振方向对反射和透射的影响。

在论文中的体现

在论文《Eikonal Rendering: Efficient Light Transport in Refractive Objects》中，作者提到：

“Although our method cannot handle polarization, it can easily cater for many other effects not treated by the above approaches, such as scattering, dispersion or volume caustics in participating media.”

具体体现

1. 偏振光的缺失：
   • 论文中明确指出，他们的方法不支持偏振光的处理。这意味着在模拟光的传播和交互时，没有考虑光的偏振方向。这可能是因为偏振光的处理会增加计算复杂度，而论文的目标是实现实时渲染。
2. 菲涅尔反射因子：
   • 论文中提到使用菲涅尔反射因子（Fresnel reflection factor）来处理非偏振光的反射：

     “$\rho$ is the Fresnel reflection factor for unpolarized light [Born and Wolf 1999].”

   • 这表明论文中使用的是简化的菲涅尔方程，适用于非偏振光，而不是偏振光的完整菲涅尔方程。
3. 反射和折射的处理：
   • 在处理反射和折射时，论文假设光是非偏振的，因此只考虑了斯涅尔定律（Snell’s Law）和菲涅尔方程的非偏振形式。这使得计算更加高效，但无法模拟偏振光的复杂行为。
4. 其他光学效果：
   • 论文主要关注折射、散射、焦散等效果，这些效果在非偏振光的假设下仍然可以很好地表现。然而，偏振光的处理可以进一步增强这些效果的逼真度，例如在某些材料（如宝石）中，偏振光可以产生更复杂的反射和折射行为。

总结

• 非偏振光与偏振光的区别：
  • 非偏振光的振动方向随机，而偏振光的振动方向有序。
  • 偏振光在通过光学元件时会表现出特定的偏振效应，而非偏振光则不会。
• 论文中的体现：
  • 论文明确指出不支持偏振光的处理，而是使用简化的菲涅尔方程处理非偏振光的反射。
  • 这种选择是为了在保持实时渲染性能的同时，实现复杂的折射和散射效果。

如果需要进一步支持偏振光，可以考虑扩展模型，引入完整的菲涅尔方程和偏振光的处理，但这会增加计算复杂度。

偏振光的详细讲解

1. 偏振光的定义

偏振光是指光波的振动方向在某个特定方向上有序排列的光。自然光（如太阳光）通常是非偏振光，其振动方向在各个方向上随机分布。通过特定的光学元件或物理过程，可以将非偏振光转化为偏振光。

2. 偏振光的类型

偏振光可以分为以下几种类型：

1. 线偏振光（Linearly Polarized Light）：
   • 光波的振动方向固定在一个平面上。例如，通过偏振片（如Polaroid滤光片）可以将自然光转化为线偏振光。
   • 线偏振光的电场矢量始终在一个方向上振动。
2. 圆偏振光（Circularly Polarized Light）：
   • 光波的振动方向在传播过程中呈圆形轨迹旋转。圆偏振光可以分为左旋圆偏振光和右旋圆偏振光。
   • 圆偏振光的电场矢量在传播方向上形成一个圆形轨迹。
3. 椭圆偏振光（Elliptically Polarized Light）：
   • 光波的振动方向在传播过程中呈椭圆形轨迹旋转。椭圆偏振光是圆偏振光和线偏振光的中间状态。
   • 椭圆偏振光的电场矢量在传播方向上形成一个椭圆形轨迹。

3. 偏振光的产生

偏振光可以通过以下几种方式产生：

1. 偏振片（Polarizer）：
   • 偏振片是一种光学元件，只允许特定方向的光通过。通过偏振片，可以将自然光转化为线偏振光。
   • 常见的偏振片材料包括Polaroid滤光片。
2. 反射和折射：
   • 当光从一种介质反射到另一种介质时，反射光可能部分偏振。例如，光在水面或玻璃表面反射时，反射光可能具有偏振特性。
   • 根据菲涅尔方程，反射光和透射光的偏振特性取决于入射角和两种介质的折射率。
3. 双折射（Birefringence）：
   • 某些晶体（如方解石）具有双折射特性，即光在晶体中沿不同方向传播时具有不同的折射率。
   • 双折射可以将入射光分解为两个偏振方向不同的光线，称为寻常光（o光）和非常光（e光）。
4. 散射：
   • 光在介质中散射时，散射光可能具有偏振特性。例如，天空中的光是部分偏振的，因为太阳光在大气中散射时产生了偏振效应。

4. 偏振光的特性

偏振光具有以下特性：

1. 偏振方向：
   • 偏振光的振动方向是固定的，可以通过偏振片或偏振滤光片检测和调整。
2. 偏振态的转换：
   • 偏振光可以通过光学元件（如半波片或四分之一波片）进行转换。例如，线偏振光可以通过四分之一波片转化为圆偏振光。
3. 偏振光的干涉：
   • 偏振光在特定条件下可以发生干涉。例如，两个偏振方向相同的光波可以发生干涉，而偏振方向不同的光波则不会干涉。
4. 偏振光的检测：
   • 偏振光可以通过偏振片检测。当偏振片的方向与偏振光的振动方向一致时，光可以完全通过；当方向垂直时，光被完全阻挡。

5. 偏振光的应用

偏振光在多个领域有广泛的应用：

1. 光学成像：
   • 偏振滤光片可以减少反射光的干扰，提高成像质量。例如，在摄影中使用偏振滤光片可以减少水面或玻璃表面的反光。
2. 显示技术：
   • 液晶显示器（LCD）利用偏振光的特性来控制光的透射，从而实现图像显示。
3. 通信技术：
   • 偏振光可以用于光通信中的数据编码，提高通信容量。
4. 材料科学：
   • 双折射和偏振光的特性可以用于研究晶体材料的光学性质。
5. 生物医学成像：
   • 偏振光成像可以用于检测生物组织的光学各向异性，例如在眼科中用于检测角膜的偏振特性。

6. 偏振光在论文中的体现

在论文《Eikonal Rendering: Efficient Light Transport in Refractive Objects》中，作者提到他们的方法不支持偏振光的处理。这表明在模拟光的传播和交互时，论文中假设光是非偏振的。具体体现如下：

1. 菲涅尔反射因子：
   • 论文中使用了菲涅尔反射因子（$\rho$）来处理非偏振光的反射，但没有考虑偏振光的完整菲涅尔方程。这表明论文中的反射和透射计算是基于非偏振光的简化模型。
2. 光的传播：
   • 论文中使用了基于Eikonal方程的光线传播模型，该模型假设光是非偏振的。因此，论文中的光线追踪和波前传播没有考虑偏振方向的影响。
3. 复杂光学效果：
   • 论文主要关注折射、散射、焦散等效果，这些效果在非偏振光的假设下仍然可以很好地表现。然而，偏振光的处理可以进一步增强这些效果的逼真度，例如在某些材料（如宝石）中，偏振光可以产生更复杂的反射和折射行为。

7. 扩展到偏振光的处理

如果需要在论文的框架中支持偏振光，可以考虑以下扩展：

1. 引入完整的菲涅尔方程：
   • 完整的菲涅尔方程可以处理偏振光的反射和透射特性。这需要在模型中引入偏振方向的描述，并计算不同偏振方向的反射和透射系数。
2. 偏振光的传播：
   • 在光线追踪和波前传播中，需要考虑偏振方向的变化。例如，通过双折射材料时，光线可能分裂为两个偏振方向不同的光线。
3. 偏振光的散射：
   • 在散射介质中，偏振光的散射特性需要根据偏振方向进行计算。这可以进一步增强散射效果的逼真度。
4. 偏振光的渲染：
   • 在渲染过程中，需要考虑偏振光的显示。例如，可以通过偏振滤光片模拟偏振光的透射和阻挡效果。

8. 总结

偏振光是指光波的振动方向在某个特定方向上有序排列的光。它可以通过偏振片、反射、折射、双折射等过程产生，并具有多种类型（线偏振光、圆偏振光、椭圆偏振光）。偏振光在光学成像、显示技术、通信技术等领域有广泛应用。

在论文《Eikonal Rendering: Efficient Light Transport in Refractive Objects》中，作者假设光是非偏振的，以简化计算并实现实时渲染。如果需要进一步支持偏振光，可以引入完整的菲涅尔方程和偏振光的传播模型，但这会增加计算复杂度。

好的！为了更深入地讲解偏振光，我们将从以下几个方面展开：

1. 偏振光的物理本质
2. 偏振光的数学描述
3. 偏振光的产生与检测
4. 偏振光的光学特性
5. 偏振光在实际应用中的体现
6. 偏振光在计算机图形学中的处理

1. 偏振光的物理本质

光是一种电磁波，其电场和磁场在垂直于传播方向的平面上振动。对于非偏振光（如自然光），电场的振动方向是随机的，而偏振光的电场振动方向是有序的，即在某个特定方向或按照某种规律变化。

• 线偏振光：电场振动方向固定在一个平面上。
• 圆偏振光：电场矢量在传播方向上形成一个圆形轨迹。
• 椭圆偏振光：电场矢量在传播方向上形成一个椭圆形轨迹。

偏振光的产生源于光的横波特性，即光的振动方向与传播方向垂直。这种特性使得光的偏振现象成为可能。

2. 偏振光的数学描述

为了描述偏振光，通常使用琼斯矢量（Jones Vector）或斯托克斯参数（Stokes Parameters）。

2.1 琼斯矢量

琼斯矢量是一个复数矢量，用于描述完全偏振光的电场振动方向和相位。对于线偏振光，琼斯矢量可以表示为： \(\mathbf{J} = \begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix}\) 其中，$\theta$ 是偏振方向与参考方向的夹角。

对于圆偏振光，琼斯矢量可以表示为： \(\mathbf{J}_{\text{左旋}} = \begin{pmatrix} 1 \\ i \end{pmatrix}, \quad \mathbf{J}_{\text{右旋}} = \begin{pmatrix} 1 \\ -i \end{pmatrix}\)

2.2 斯托克斯参数

斯托克斯参数用于描述部分偏振光或非偏振光的偏振状态。它们由四个参数组成：$S_0, S_1, S_2, S_3$，其中：

• $S_0$ 表示总光强。
• $S_1$ 表示水平偏振与垂直偏振的差值。
• $S_2$ 表示对角偏振的差值。
• $S_3$ 表示圆偏振的差值。

通过斯托克斯参数，可以全面描述光的偏振状态，包括偏振度和偏振方向。

3. 偏振光的产生与检测

3.1 偏振光的产生

偏振光可以通过以下几种方式产生：

1. 偏振片（Polarizer）：
   • 偏振片是一种光学元件，只允许特定方向的光通过。通过偏振片，可以将自然光转化为线偏振光。
   • 常见的偏振片材料包括Polaroid滤光片。
2. 反射和折射：
   • 当光从一种介质反射到另一种介质时，反射光可能部分偏振。例如，光在水面或玻璃表面反射时，反射光可能具有偏振特性。
   • 根据菲涅尔方程，反射光和透射光的偏振特性取决于入射角和两种介质的折射率。
3. 双折射（Birefringence）：
   • 某些晶体（如方解石）具有双折射特性，即光在晶体中沿不同方向传播时具有不同的折射率。
   • 双折射可以将入射光分解为两个偏振方向不同的光线，称为寻常光（o光）和非常光（e光）。
4. 散射：
   • 光在介质中散射时，散射光可能具有偏振特性。例如，天空中的光是部分偏振的，因为太阳光在大气中散射时产生了偏振效应。

3.2 偏振光的检测

偏振光可以通过以下几种方式检测：

1. 偏振片：
   • 通过偏振片可以检测光的偏振方向。当偏振片的方向与偏振光的振动方向一致时，光可以完全通过；当方向垂直时，光被完全阻挡。
2. 偏振分束器（Polarizing Beam Splitter）：
   • 偏振分束器可以将入射光分为两个偏振方向不同的光束，从而用于测量光的偏振态。
3. 偏振光度计（Polarimeter）：
   • 偏振光度计是一种专门用于测量光的偏振态的仪器，可以测量斯托克斯参数，从而确定光的偏振度和偏振方向。

4. 偏振光的光学特性

4.1 菲涅尔方程

菲涅尔方程描述了光在两种介质界面处的反射和透射特性。对于偏振光，菲涅尔方程需要考虑偏振方向的影响。例如：

• 平行偏振光（p-polarized light）： \(R_p = \left| \frac{n_1 \cos\theta_i - n_2 \cos\theta_t}{n_1 \cos\theta_i + n_2 \cos\theta_t} \right|^2\)
• 垂直偏振光（s-polarized light）： \(R_s = \left| \frac{n_1 \cos\theta_t - n_2 \cos\theta_i}{n_1 \cos\theta_t + n_2 \cos\theta_i} \right|^2\) 其中，$n_1$ 和 $n_2$ 是两种介质的折射率，$\theta_i$ 是入射角，$\theta_t$ 是折射角。

4.2 偏振光的干涉

偏振光在特定条件下可以发生干涉。例如，两个偏振方向相同的光波可以发生干涉，而偏振方向不同的光波则不会干涉。这种特性在偏振光学中非常重要，例如在液晶显示器（LCD）中，偏振光的干涉用于控制光的透射。

4.3 偏振光的散射

偏振光在散射介质中传播时，散射光的偏振特性会受到散射过程的影响。例如，光在大气中的散射会导致部分偏振光的产生。这种偏振特性可以用于大气光学的研究，例如通过测量天空光的偏振度来推断大气中的气溶胶分布。

5. 偏振光在实际应用中的体现

5.1 光学成像

偏振光在光学成像中有广泛应用，例如：

• 偏振滤光片：可以减少反射光的干扰，提高成像质量。例如，在摄影中使用偏振滤光片可以减少水面或玻璃表面的反光。
• 偏振显微镜：用于观察生物组织或材料的偏振特性，例如检测晶体的双折射现象。

5.2 显示技术

液晶显示器（LCD）利用偏振光的特性来控制光的透射，从而实现图像显示。LCD屏幕由两片偏振片和液晶层组成，通过控制液晶分子的排列，可以改变光的偏振态，从而实现灰度和色彩的显示。

5.3 通信技术

偏振光可以用于光通信中的数据编码，提高通信容量。例如，通过使用两个正交偏振方向的光波，可以在同一信道中传输更多的数据。

5.4 生物医学成像

偏振光成像可以用于检测生物组织的光学各向异性，例如在眼科中用于检测角膜的偏振特性。此外，偏振光成像还可以用于皮肤成像，检测皮肤中的胶原蛋白分布。

6. 偏振光在计算机图形学中的处理

在计算机图形学中，偏振光的处理可以显著增强渲染的真实感。然而，偏振光的计算复杂度较高，因此在实时渲染中通常不考虑偏振效应。论文《Eikonal Rendering: Efficient Light Transport in Refractive Objects》中提到，他们的方法不支持偏振光的处理，但可以处理其他复杂效果，如散射、焦散等。

6.1 扩展到偏振光的处理

如果需要在计算机图形学中支持偏振光，可以考虑以下扩展：

1. 引入完整的菲涅尔方程：
   • 完整的菲涅尔方程可以处理偏振光的反射和透射特性。这需要在模型中引入偏振方向的描述，并计算不同偏振方向的反射和透射系数。
2. 偏振光的传播：
   • 在光线追踪和波前传播中，需要考虑偏振方向的变化。例如，通过双折射材料时，光线可能分裂为两个偏振方向不同的光线。
3. 偏振光的散射：
   • 在散射介质中，偏振光的散射特性需要根据偏振方向进行计算。这可以进一步增强散射效果的逼真度。
4. 偏振光的渲染：
   • 在渲染过程中，需要考虑偏振光的显示。例如，可以通过偏振滤光片模拟偏振光的透射和阻挡效果。

7. 总结

偏振光是指光波的振动方向在某个特定方向上有序排列的光。它可以通过偏振片、反射、折射、双折射等过程产生，并具有多种类型（线偏振光、圆偏振光、椭圆偏振光）。偏振光在光学成像、显示技术、通信技术等领域有广泛应用。

在计算机图形学中，偏振光的处理可以显著增强渲染的真实感，但计算复杂度较高。如果需要支持偏振光，可以引入完整的菲涅尔方程和偏振光的传播模型，但这会增加计算复杂度。

菲涅尔定律（Fresnel Equations）

菲涅尔定律描述了光在两种介质界面处的反射和透射特性。这些定律是基于麦克斯韦方程组推导出来的，用于计算入射光在界面上的反射率和透射率。菲涅尔定律有两种形式：一种适用于非偏振光，另一种适用于偏振光。

1. 非偏振光的菲涅尔定律

对于非偏振光，菲涅尔定律通常给出的是平均反射率和平均透射率。非偏振光的反射率可以通过以下公式计算：

\[R = R_s = R_p = \left| \frac{n_1 \cos \theta_i - n_2 \cos \theta_t}{n_1 \cos \theta_i + n_2 \cos \theta_t} \right|^2\]

其中：

• ( n_1 ) 和 ( n_2 ) 分别是两种介质的折射率。
• ( \theta_i ) 是入射角。
• ( \theta_t ) 是折射角，可以通过斯涅尔定律计算： \(n_1 \sin \theta_i = n_2 \sin \theta_t\)

在这种情况下，反射率 ( R ) 是一个标量值，表示反射光的强度与入射光的强度之比。非偏振光的反射率不依赖于偏振方向，因此在实际应用中，通常使用这个简化的公式来计算反射率。

2. 偏振光的菲涅尔定律

对于偏振光，菲涅尔定律需要分别考虑平行偏振光（p-polarized light）和垂直偏振光（s-polarized light）的反射率和透射率。这是因为这两种偏振方向的光在界面上的行为是不同的。

2.1 平行偏振光（p-polarized light）

平行偏振光的电场振动方向平行于入射平面。其反射率 ( R_p ) 和透射率 ( T_p ) 可以通过以下公式计算：

\[R_p = \left| \frac{n_1 \cos \theta_i - n_2 \cos \theta_t}{n_1 \cos \theta_i + n_2 \cos \theta_t} \right|^2\] \[T_p = \frac{2 n_1 \cos \theta_i}{n_1 \cos \theta_i + n_2 \cos \theta_t}\]

2.2 垂直偏振光（s-polarized light）

垂直偏振光的电场振动方向垂直于入射平面。其反射率 ( R_s ) 和透射率 ( T_s ) 可以通过以下公式计算：

\[R_s = \left| \frac{n_1 \cos \theta_t - n_2 \cos \theta_i}{n_1 \cos \theta_t + n_2 \cos \theta_i} \right|^2\] \[T_s = \frac{2 n_1 \cos \theta_i}{n_1 \cos \theta_t + n_2 \cos \theta_i}\]

3. 非偏振光与偏振光的菲涅尔定律对比

3.1 非偏振光

• 反射率：使用单一公式计算，不区分偏振方向。
• 适用场景：适用于自然光或未经过偏振处理的光。
• 优点：计算简单，适用于大多数实时渲染场景。

3.2 偏振光

• 反射率：需要分别计算 ( R_p ) 和 ( R_s )，考虑偏振方向的影响。
• 适用场景：适用于需要精确模拟偏振效应的场景，如高级光学系统、偏振成像等。
• 优点：能够更精确地模拟光在界面上的行为，尤其是在涉及偏振片、双折射材料等情况下。
• 缺点：计算复杂度较高，需要更多的计算资源。

4. 在计算机图形学中的应用

在计算机图形学中，菲涅尔定律通常用于计算物体表面的反射光和透射光。对于大多数实时渲染应用，非偏振光的菲涅尔定律已经足够使用，因为它能够提供较为逼真的反射效果，同时计算效率较高。

然而，如果需要模拟更复杂的光学现象，如偏振滤光片、偏振成像或双折射材料，就需要使用偏振光的菲涅尔定律。这可以通过引入琼斯矢量或斯托克斯参数来描述偏振光的状态，并在渲染过程中动态计算反射和透射光的偏振特性。

5. 总结

• 非偏振光的菲涅尔定律：适用于大多数实时渲染场景，计算简单，不区分偏振方向。
• 偏振光的菲涅尔定律：适用于需要精确模拟偏振效应的场景，计算复杂度较高，但能够更精确地模拟光在界面上的行为。

在实际应用中，选择哪种形式的菲涅尔定律取决于具体的渲染需求和计算资源。对于大多数场景，非偏振光的菲涅尔定律已经足够；而对于高级光学模拟，偏振光的菲涅尔定律是必不可少的。

原文翻译

《Eikonal Rendering: Efficient Light Transport in Refractive Objects》

Ivo Ihrke¹, Gernot Ziegler¹, Art Tevs¹, Christian Theobalt¹, Marcus Magnor², Hans-Peter Seidel¹
¹) Max-Planck-Institut für Informatik
²) Technical University Braunschweig

摘要

我们提出了一种用于实时渲染复杂折射物体及其周围复杂光照效果的新方法。该方法能够逼真地显示具有复杂材质属性的折射物体，例如任意变化的折射率、非均匀吸收以及空间变化的各向异性散射和反射属性。用户控制的光源位置更改仅需几秒的更新时间。我们的方法基于从几何光学的基本假设——Eikonal方程推导出的一组常微分方程。这组方程允许我们以粒子追踪的复杂度快速投射弯曲的光线。基于这一概念，我们还提出了一种使用自适应波前追踪的高效光照传播技术。我们为算法概念提供了高效的GPU实现，从而能够实时渲染以前无法实现的多种视觉效果组合。

CR分类: I.3.7 [三维图形与逼真度]

关键词: 折射物体、实时渲染、光照传输、几何光学

图1：复杂折射物体的实时渲染——（左）装有红葡萄酒的玻璃杯投射出色彩斑斓的焦散，帧率为24.8fps。（中）琥珀色兔子带有黑色嵌入物，展示周围烟雾及其内部的各向异性散射和体积焦散，帧率为13.0fps。（右）由三种不同颜色和不同折射率的玻璃组成的圆润立方体，展示其内部的散射效果和焦散，帧率为6.4fps。

1 引言

具有复杂光学特性的物体，例如装满葡萄酒的水晶玻璃，看起来非常迷人。这种迷人的视觉效果来源于这些物体内部、表面及其周围可见的光线和色彩效果的美感。这种视觉美感的物理根源在于光与物质相互作用过程的复杂性，这些过程发生在光线穿过物质边界、在物体内部传播以及与物体周围环境相互作用时。在物质边界处，光线可能会以复杂的方式反射和透射。空间变化的折射率，可能与复杂的表面反射率相结合，会导致光线的非均匀聚焦，从而形成美丽的表面和体积焦散。某些材料表现出空间变化或与波长相关的衰减特性，这会导致色彩的偏移。此外，各向异性散射效应也会极大地影响物体的整体外观。

本文的贡献在于提出了一个通用框架，能够在普通图形硬件上实时复现上述大多数效果。我们的图像生成模型支持渲染包含任意变化折射率的物体、具有任意BRDF的表面效果以及具有任意散射相函数的视图依赖单次散射效果的复杂光线路径。高级效果，如全反射，可以在不增加额外成本的情况下隐式获得。此外，我们的渲染器能够复现折射表面和体积焦散，并真实地渲染在散射介质（如烟雾）中的半透明物体的外观。

接下来，我们首先介绍一个基于体积场景表示的通用图像生成模型，该模型考虑了所有这些效果（第3节）。随后，我们描述了将该模型高效映射到GPU的简化方法。为了快速模拟光的传输，我们采用了一组从Eikonal方程推导出的简单常微分方程，这是几何光学的主要假设。我们的方法能够使用同一优雅的数学框架，从光源和向观察者方向评估复杂的光线路径。每个光源在场景中的辐照度分布通过基于波前的光照传播方案快速预计算（第4节）。最后，我们提出了新的概念和动态数据结构，以高效地在普通图形硬件上评估我们的图像生成模型（第5节）。在第6节中，我们展示了我们的原型GPU渲染器在折射物体周围实时显示上述各种效果的结果。

2 相关工作

在文献中已经发表了几种方法，可以在GPU上实时近似折射效果[Wyman 2005]，在专用信号处理器上实现[Ohbuchi 2003]，或者在基于CPU的实时光线追踪器中实现[Wald et al. 2002]。Hakura和Snyder [2001]提出了一种基于混合光线追踪的方法，能够产生吸引人的结果，但无法实时运行。这些算法大多通过在物质边界处计算斯涅尔定律（Snell’s law）来获得良好的效果。关于非均匀折射率分布的渲染主要出现在模拟大气效应的文献中。Berger等人[1990]通过在离线渲染器中反复应用斯涅尔定律来光线追踪海市蜃楼。Musgrave [1990]在其工作中加入了全反射现象，用于渲染相同的效应。Stam和Languénou [1996]提出使用几何光学的光线方程来渲染热闪烁效果。最近，Gutierrez等人[2006]也将光线方程应用于渲染海市蜃楼和其他大气效应。Zhao等人[2007]在GPU上模拟并以交互帧率渲染热闪烁和海市蜃楼。Guy和Soler [2004]提出了一种显示宝石的方法，能够处理折射和偏振效应。尽管我们的方法无法处理偏振，但它可以轻松实现上述方法未涉及的许多其他效果，例如散射、色散或介质中的体积焦散。

折射渲染与渲染逼真焦散的问题密切相关。高质量焦散渲染的流行离线方法包括反向光线追踪[Arvo 1986]和光子映射[Jensen et al. 2001]，后者也可以生成体积焦散[Jensen and Christensen 1998]。这些方法通过在空间存储数据结构中存储光子能量，并在图像生成过程中收集它们的贡献来实现。Gutierrez等人[2005]将体积光子映射扩展到非线性光路径，使用几何光学的光线方程来模拟大气和水下场景中的折射效应。除了本文中处理的效果外，他们还在离线渲染器中渲染了多次非弹性散射事件。实时光线追踪系统[Parker et al. 1999; Carr et al. 2002; Wald et al. 2002]能够在交互帧率下渲染离散界面处的折射和光子映射[Wyman et al. 2004]，但通常需要一个PC集群[Günther et al. 2004]来处理计算负载。

最近，研究人员将这些算法移植到图形硬件上以实现实时性能。Wand和Strasser [2003]通过用均匀采样的光源近似表面来计算反射焦散。Wyman和Davis [2006]提出了一种与光子映射相关的GPU上交互式近似焦散渲染的图像空间技术。他们还提出了一个类似于Nishita和Nakamae [1994]的光照体积的光束结构，用于近似空间中光束的光强分布。Ernst等人[2005]也采用了类似的概念来生成表面和体积焦散。

与上述技术相比，我们采用了一个更通用的光传输模型，该模型沿任意轨迹传播具有任意复杂折射特性的波前。通过在采样的3D体积中计算辐照度分布，可以生成表面和体积焦散。我们还能够为空间中的每个点获取局部光方向，从而实现各向异性光照效果的渲染。我们的图像生成流程基于几何光学理论，结合强大的图像生成模型，能够真实地处理多种额外效果，例如色散、发射、散射、BRDF和空间变化的吸收，所有这些都在一个通用框架内实现。

关于体积场景描述中的光散射最早由Blinn [1982]引入到计算机图形学中。Kajiya和von Herzen [1984]推导出基于体积密度的散射一般公式，并提出了单次和多次散射的一般方程。我们在图像生成模型中使用了他们的单次散射方程。Rushmeier和Torrance [1987]在辐射度风格的算法中处理了表面与体积之间的光照交互。Stam [1995]探讨了多次散射的极限，并提出了这种极限的扩散近似。最近，出现了实时单次散射的实现方法。Magnor等人[2005]使用GPU光线投射方法来渲染反射星云——这种方法与我们的散射、发射和吸收实现最为相似，但它使用的是直线视线和光线。Mertens等人[2003]使用Jensen等人[2001]的模型实时渲染单次次表面散射和多次散射的偶极近似。尽管我们没有近似多次散射，但我们沿着复杂的非线性光路径渲染单次各向异性散射。

我们光传播方案的基本概念来源于几何光学的Eikonal方程和传输方程[Born and Wolf 1999]。弯曲的视线是根据几何光学的光线方程计算的，这与用于模拟引力透镜的非线性光线追踪[Gröller 1995; Weiskopf et al. 2004]类似。为了在体积中预计算辐照度分布，我们采用自适应波前追踪方法。基于波前的辐照度估计技术在计算机图形学中很少使用。Mitchell和Hanrahan [1992]通过分析计算费马路径，并根据沿计算路径跟踪的波前曲率来评估表面的辐照度。Collins [1994]从光源追踪光线，并通过检查光线击中漫反射表面的分布来评估波前行为。Bri`ere和Poulin [2000]建议使用光束追踪来离线渲染表面和体积焦散。辐照度估计基于几何光学的强度定律。

总结而言，我们提出了一个基于Eikonal方程的新快速且通用框架，能够联合复现复杂折射物体周围的多种光照效果，而在此之前，需要单独的专用算法才能实现实时帧率。

3 图像生成模型

3.1 通用图像生成

我们关注于具有变化材质的透明物体的逼真且高效的渲染。为此，我们假设复杂的材质分布存储在一个三维体积中。我们的通用图像生成模型考虑了发射、吸收、反射和散射。对于穿过体积的特定光线（可能是弯曲的），其数学表达式为：

\[L(c) = \int_c L_c(x, v)\alpha(t, c)dt + L_{\text{bg}}\alpha(t_\infty, c), \quad (1)\]

其中，$L_c$ 表示沿光线 $c$ 散射、发射或反射到观察方向的辐射亮度，$L_{\text{bg}}$ 是背景辐射亮度，$\alpha(t, c)$ 是沿光线位置 $t$ 处的光吸收。$L_c$ 由不同成分组成，这些成分对给定光线的辐射亮度有贡献。函数 $L_c$ 依赖于空间位置 $x = c(t)$ 和局部光线方向 $v = \frac{dc}{dt}$。一般来说，它是波长依赖的，并且可以使用每个波长 $\lambda$ 的不同参数进行计算。我们可以用这些变量表示 $L_c$：

\[L_c(x, v) = \hat{\omega}L_s(x, v) + \delta(x)\rho L_r(x, v) + L_e(x, v). \quad (2)\]

这里，$L_s$ 表示由于散射引起的辐射亮度，$\hat{\omega} = \frac{\sigma_s}{\sigma_a + \sigma_s}$ 是参与介质的反照率，$L_r$ 是反射到观察方向的辐射亮度，$L_e$ 是局部发射的辐射亮度。狄拉克函数 $\delta(x)$ 作为边界指示器，即在两个不同物体的边界上积分值为1，而在其他地方为0。这说明反射发生在不同材质的边界上。$\rho$ 是非偏振光的菲涅尔反射因子[1]。菲涅尔透射因子 $\tau$ 通过因子 $T(t)$ 进入吸收方程（5），我们稍后将描述。

$L_s$、$L_r$ 和 $L_e$ 都依赖于空间位置 $x$ 和局部光线方向 $v$，并且可以根据它们的分布的体积描述进行局部评估。最后一点很重要。给定适当的预计算，$L_c$ 的局部性允许我们以高效的方式并行化计算。

我们用散射相函数 $p$ 来表示散射：

\[L_s(x, v) = \int_\Omega p(x, v, \omega)dE_\omega. \quad (3)\]

由于散射的光贡献在入射方向的球面上积分，从而得到 $L_s$。类似地，我们写出：

\[L_r(x, v) = \int_{\Omega^+} f_r(x, v, \omega)\cos\theta dE_\omega, \quad (4)\]

其中，$f_r$ 描述了一个双向反射分布函数（BRDF），$\cos\theta$ 是表面法线与入射光方向 $\omega$ 之间的夹角的余弦值。表面法线可以作为一个额外的函数提供，或者从折射率场 $n$ 中推导出来。因此，$L_r$ 给出了由于反射而产生的辐射亮度贡献。请注意，这一项仅在物体的边界上有效，其贡献由 $\delta(x)$ 触发。

$L_e$ 以其最一般的形式是一个函数 $L_e(x, v)$。结合光源定义，它可以用来模拟多次散射效应或由于荧光或磷光引起的自发射。

最后，我们详细考察方程（1）中的吸收函数 $\alpha$。如果考虑任意的吸收分布，它依赖于沿光线的距离和光线的形状，因此可以表示为：

\[\alpha(t, c) = T(t)e^{-\int_0^t \sigma_t(c(s))ds}, \quad (5)\]

即吸收函数描述了由于空间变化的衰减函数 $\sigma_t = \sigma_a + \sigma_s$，在位置 $x = c(t)$ 处辐射亮度的指数衰减，其中 $\sigma_a$ 是吸收系数，$\sigma_s$ 是描述由于散射而丢失的辐射亮度的散射系数。$T(t)$ 是沿光线到位置 $t$ 遇到的所有菲涅尔透射因子 $\tau$ 的乘积。

3.2 简化图像生成

在其一般形式下，我们的图像生成模型过于复杂，无法实时评估。因此，我们做出两个简化假设：

1. 场景中的光来源于有限数量的光源，且

2. 对于场景中的每个点，每个光源仅存在有限数量的入射光线。

这些限制使我们能够为相当复杂的图像生成模型开发高效的渲染算法，因为我们可以将方程（3）和（4）中的积分转换为对所有入射光方向的离散求和：

\[L_s(x, v) = \sum_j p(x, v, l_j)\Delta E_{\omega j}, \quad (6)\] \[L_r(x, v) = \sum_j f_r(x, v, l_j) \cos\theta \Delta E_{\omega j}. \quad (7)\]

因此，如果我们能够预计算入射光方向和微分辐照度值，我们就可以仅通过局部操作来评估方程（1）。在接下来的部分中，我们将推导视图光线遍历和辐照度计算的数学公式。

4 光传输

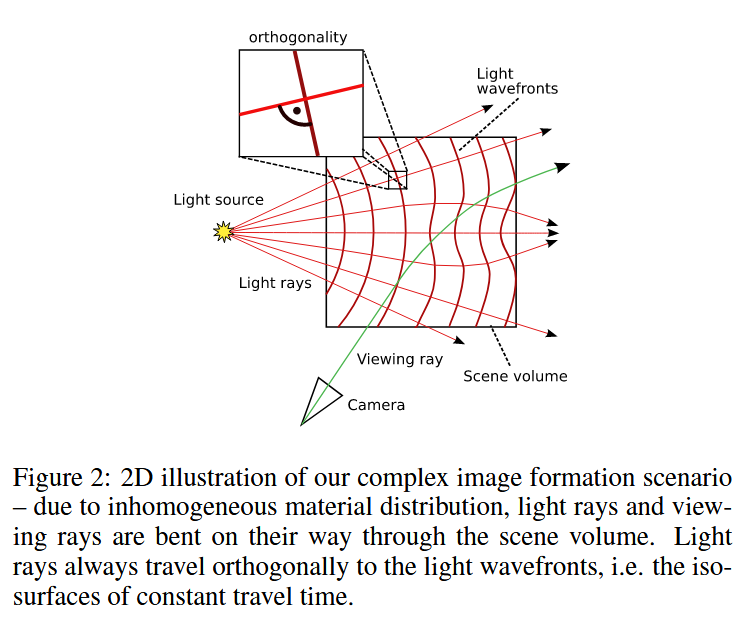
图2：我们复杂图像生成场景的二维示意图——由于材料分布不均匀，光线和视线在穿过场景体积时发生弯曲。光线始终垂直于光波前传播，即沿着等时面（常数传播时间的等值面）传播。

在本节中，我们推导场景中光传输的方程。视图光线的传播在第4.1节中描述，而光传输在第4.2节中讨论。视图光线和光线的行为非常相似（如图2所示），其控制方程均来源于几何光学的光线方程[Born and Wolf 1999]。然而，我们使用不同的参数化方法来考虑这两个过程的具体特性。请注意，对于光线，我们需要考虑辐照度的衰减，而视图光线携带的是辐射亮度。

4.1 视图光线传播

几何光学的光线方程已在计算机图形学中被使用，例如Stam和Languénou [1996]以及Gutierrez等人[2005]的工作。该方程描述了光“粒子”在非均匀折射率场 $n$ 中的运动：

\[\frac{d}{ds}\left(n \frac{dx}{ds}\right) = \nabla n. \quad (8)\]

该方程由Eikonal方程推导而来，描述了无质量粒子沿Eikonal解的梯度运动。$ds$ 表示沿弯曲光线切线方向的无穷小步长。

方程（8）可以重写为一组一阶常微分方程：

\[\frac{dx}{ds} = \frac{v}{n}, \quad (9)\] \[\frac{dv}{ds} = \nabla n. \quad (10)\]

这些方程可以通过简单的欧拉前向方案离散化：

\[x_{i+1} = x_i + \Delta s \cdot \frac{v_i}{n}, \quad (11)\] \[v_{i+1} = v_i + \Delta s \cdot \nabla n, \quad (12)\]

或者使用更高阶的积分方法，如龙格-库塔族方法[Press et al. 1992]。方程（9）和（10）具有所有光线轨迹的空间步长相等的特性，证明见附录。这一特性在渲染中（第5节）具有优势，因为在渲染中每个粒子追踪的迭代次数应大致相等，以确保最佳性能。此外，光线弯曲和全反射自然地由几何光学的光线方程支持。

4.2 光源建模

我们用三维向量场表示局部光方向 $l(x)$ 和标量场表示微分辐照度值 $\Delta E_\omega(x)$ 来建模光源（参见第3.2节）。这些场可以通过多种方法计算。在计算机图形学研究者中，流行的选择是光子映射[Jensen 2001]，其GPU实现也已存在[Purcell et al. 2003]。在计算物理和数值分析的文献中，提出了大量解决这一问题的方法。这些方法包括：仅使用Eikonal方程和传输方程的欧拉格式[Buske and Kästner 2004]、相空间方法[Osher et al. 2002]、混合拉格朗日-欧拉方法[Benamou 1996]，以及自适应波前追踪[Enquist and Runborg 2003]。除了纯欧拉方法外，所有方法都处理了底层方程解的固有多值性。

我们选择自适应波前追踪[Enquist and Runborg 2003; Collins 1997]来计算局部光方向和微分辐照度值，因为它在计算时间和解的准确性之间提供了最佳折衷。波前是从光源发出的光的等时面（参见图2）。根据费马原理，光线总是垂直于这些波前传播。波前通过一组相互连接的粒子进行离散化，这些粒子在非均匀折射率场中传播。如果波前变得欠采样，就会插入新的粒子以保持最小采样率（参见图4）。局部光方向由粒子的传播方向表示，微分辐照度值可以从波前片的面积计算（参见第4.2.2节）。

三维光分布的预计算包括以下连续步骤：

I. 波前传播，

II. 辐照度计算，

III. 波前细化，

IV. 局部光方向和微分辐照度值的体素化。

这个过程会一直重复，直到波前离开感兴趣的体积。以下详细说明各个步骤。

4.2.1 波前传播

我们将波前离散化为一组相互连接的粒子，这些粒子独立传播。这样，波前被细分为所谓的波前片，其角点由光粒子定义（参见图4右）。连接信息用于微分辐照度计算。粒子的传播按照方程（8）进行，类似于视线传播（第4.1节）。我们对其进行重新参数化以实现等时离散化步骤：

\[n \frac{d}{dt}\left(\frac{n^2 dx}{dt}\right) = \nabla n. \quad (13)\]

附录中给出了这一性质的证明。重新参数化是必要的，以便于在第4.2.2节中描述的微分辐照度计算的简单表述。它确保所有粒子随时间保持在同一个波前上，这对于应用几何光学的简单强度定律是必要的，而不是像[Mitchell and Hanrahan 1992; Collins 1994]中那样跟踪波前曲率。类似于方程（9）和（10），我们可以将方程（13）写成一组一阶常微分方程：

\[\frac{dx}{dt} = \frac{v}{n^2}, \quad (14)\] \[\frac{dv}{dt} = \frac{\nabla n}{n}. \quad (15)\]

这种表述使得波前传播方案可以作为粒子追踪器快速在GPU上实现。一旦可以随时间跟踪波前，我们就可以通过连接粒子的波前片的面积计算空间中每一点的微分辐照度。

4.2.2 辐照度计算

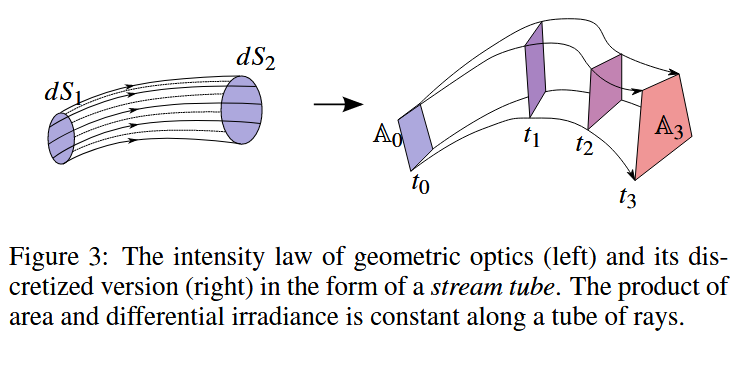
图3：几何光学的强度定律（左）及其离散化版本（右），以流管的形式表示。沿光线管的面积与微分辐照度的乘积保持不变。

辐照度计算基于几何光学的强度定律[Born and Wolf 1999]，见图3（左）。该定律指出，在一个无穷小的光线管中，能量保持不变：

\[dE_{\omega1} dS_1 = dE_{\omega2} dS_2. \quad (16)\]

我们使用强度定律的离散版本来更新波前片在传播过程中的能量贡献。每个波前片在场景中的运动描述了一个所谓的流管，见图3（右）。因此，方程（16）可以写为：

\[\Delta E_\omega(t) = \Delta E_\omega(0) \frac{A(0)}{A(t)}. \quad (17)\]

这里，$A(t)$ 表示时间 $t$ 时波前片的面积，$\Delta E_\omega(t)$ 是与之相关的离散微分辐照度。由于我们在图像生成模型中模拟了吸收效应，因此这一效应也必须包含在辐照度计算中。因此，波前片的最终离散微分辐照度为：

\[\Delta E_\omega(t) = \Delta E_\omega(0) \frac{A(0)}{A(t)} e^{-\int_0^t \sigma_t(c(n(\hat{t}))) d\hat{t}}. \quad (18)\]

4.2.3 波前细化与体素化

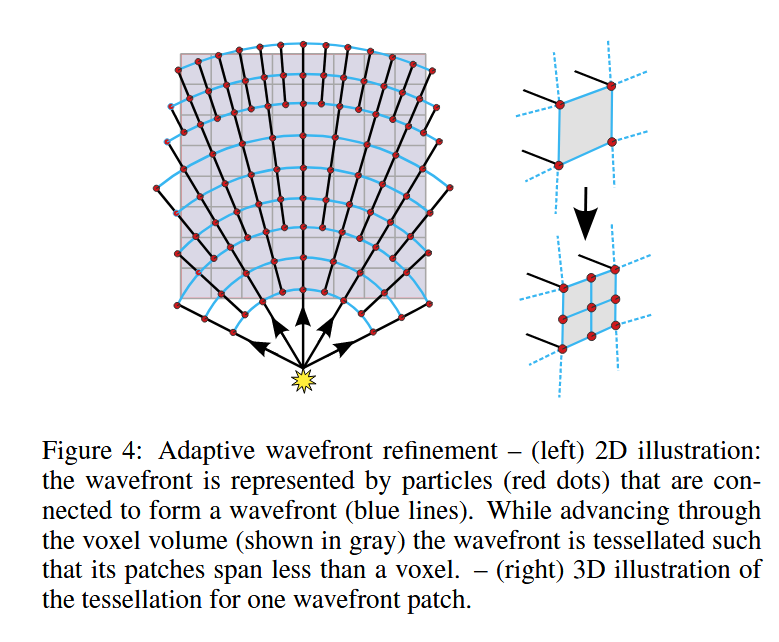
图4：自适应波前细化——（左）二维示意图：波前由粒子（红色点）表示，这些粒子连接形成波前（蓝色线）。在穿过体素体积（灰色显示）时，波前被细分，使其片元小于一个体素。（右）一个波前片的三维细分示意图。

为了获得光分布的连续体积表示，波前片需要被体素化。然而，由于波前片的角点可能会发散，它们在传播过程中通常会变得任意地大。如果一个波前片的面积滑过一个体素而没有触及该体素的任何一个角点，它实际上会忽略该体素的折射率值。因此，波前会被欠采样。为了解决这一问题，我们在波前片的面积超过一个体素时对其进行自适应分割，见图4。由于图形硬件无法将任意大小的四边形光栅化到三维体积中，我们使用自适应采样，并将波前片与其中心点等同起来，将微分辐照度和方向信息存储为单个体素样本。因此，波前的欠采样问题与基于GPU的体素化实现同时得到了解决。

5 实现问题

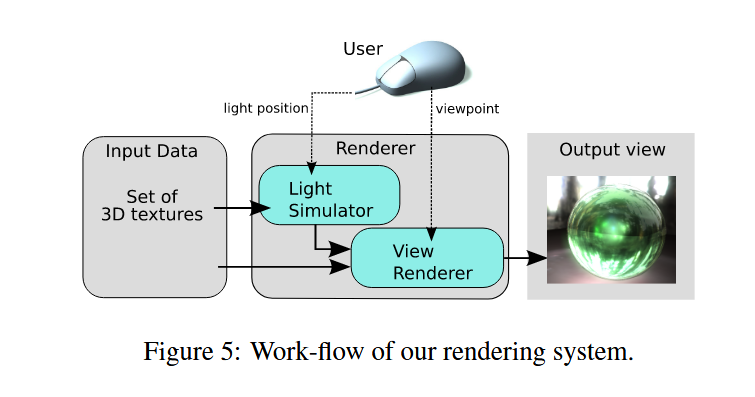
图5：我们渲染系统的流程图。

在奠定了理论基础之后，我们现在详细探讨如何将上述概念映射到GPU上。图5展示了我们渲染器的工作流程。接下来，我们将详细介绍其最重要的组成部分：所采用的数据格式（第5.1节）、光源模拟器（第5.2节）以及视图渲染器（第5.3节）。

5.1 输入数据格式

输入场景被存储为一组三维体积纹理。在第一组体积中，存储了空间变化的折射率场及其梯度场。我们测试场景中的物体是以旋转体、隐式曲面或三角网格的形式创建的，并将它们光栅化到三维体积中。折射率分布可以直接从物体的隐式函数中导出，也可以通过交互式方式定义。在计算梯度之前，我们会对体积进行平滑处理。我们使用标准差通常为0.5到1.0体素的均匀高斯滤波器内核，这使得物体边界扩展到2到3个体素。通过使用合适的代理几何体来启动光线投射，可以缓解边界模糊的问题。尽管这种方法可以提高边界的清晰度并带来更高的帧率，但物体周围的参与介质将无法再被渲染。

其他三维纹理包含了空间变化的RGB吸收函数、材质边界指示器以及BRDF参数或发射描述。边界指示器是方程（2）中狄拉克δ函数的离散版本。我们通过对网格进行体素化或使用折射率梯度的梯度强度来计算它。对于我们的部分测试物体，我们通过应用噪声函数或将它绘制到旋转曲面的二维输入中，来模拟物体内部的空间变化吸收。为了近似各向异性散射效应，我们采用了Henyey和Greenstein [1941]的散射相函数模型，其参数也被存储在体积纹理中。

5.2 光源模拟器

我们的实现遵循第4节中描述的自适应波前传播。然而，由于我们希望在Shader Model 4.0之前的硬件上也能实现高效的模拟，因此我们引入了一些额外的概念。

在光源处初始化后，波前被表示为一个粒子系统。与标准粒子系统的区别在于，粒子被绑定成四组，从而形成了波前片（见图4右）。这使得我们能够在图形硬件上模拟流管概念。所有波前片都被存储在纹理中，这些纹理保存了四个角的位置、它们的传播方向以及一个RGB能量值（见第4.2.2节）。

在初始化过程中，我们使用波前片列表纹理的二维参数化来生成平面波前（用于方向光源）或球面波前（用于点光源）。初始化确保波前足够大，能够覆盖整个模拟体积。其他类型的光源（如多向光源）也可以实现，因为波前片是独立的，因此可以将它们堆叠在一起。波前在场景中的传播以及记录到输出三维体积中的过程分为以下三个连续步骤。

5.2.1 波前片更新

在每个时间步中，我们根据方程（14）和（15）更新波前片的角点位置和方向。此外，我们还根据方程（18）更新波前片所持有的RGB能量值。

5.2.2 波前片体素化

在每次更新步骤之后，我们需要将波前片记录到三维输出体积中，用于存储辐照度和方向信息。在图形硬件上，这一过程通过使用点基元和由Harris等人[2003]引入的Flat 3D纹理概念来实现。我们仅限于存储每个体素处对应于最高能量光线的一个入射光方向。这一选择是基于统计分析的合理性：对于酒杯模型（见图8右），只有5.6%的体素从多个方向接收光线，而在这些体素中，最高能量的光线平均贡献了到达这些体素总能量的81.6%。其他模型也显示出类似的结果。在将一个波前片写入三维体积之前，我们会根据最高能量标准检查是否允许覆盖已存储的波前片（如果存在）。

5.2.3 波前片细分分析

在每次模拟步骤之后，由于各种原因，需要重新组织波前片列表：

发散细分：由于波前在折射率变化的地方会发散，因此需要对其进行细分以保持最小采样界限，如第4.2节所述。此外，由于GPU体素化的限制，大于一个体素的波前片也需要进行细分。目前，我们的简单细分策略是，如果一个波前片的角点在任何方向上跨越超过一个体素，则将其划分为四个更小的波前片，如图4所示。

波前片终止：如果一个波前片的能量过低，我们会应用能量阈值来消除该波前片，假设它不会再收缩，因此也不会再产生显著的能量贡献。终止通常发生在经过过多细分或由于反复衰减导致能量损失过多之后。我们还会消除那些离开模拟体积的波前片，因为我们假设它们不会再重新进入模拟体积。光线光学的物理模型在波前奇点处会失效[Born and Wolf 1999]，导致在灾难性点处出现无限能量，从而产生非物理的焦散。我们通过检查波前片的方向相对于其传播方向的变化来检测这些区域。如果方向发生变化，则表明波前片已经穿过了一个奇点，我们将它从后续模拟中丢弃。

实际上，这意味着一个波前片可以处于三种状态之一：消除（0）、保留（1）或细分（4）。括号中的数字定义了每个输入波前片在为下一步模拟生成的输出波前片列表中所占据的空间。我们在更新波前片角点方向之后进行细分分析。因此，我们需要重新组织波前片列表，这面临着在图形硬件上进行数据压缩和扩展的非平凡问题。数据压缩（即波前片消除）已经在Ziegler等人[2006]提出的GPU算法中得到解决。该算法使用类似mipmap的数据结构——HistoPyramid，在不涉及CPU的情况下构建保留的数据条目列表（此处为波前片）。我们将该算法扩展到处理波前片细分（数据扩展）。它利用了这样一个事实：如果输入条目在HistoPyramid构建过程中被标记为大于1的值，则原始算法会为该输入条目分配多个输出位置。这将产生输入条目的多个副本。而不是简单地接收四个相同的波前片副本，我们在输出生成器中引入特定行为，将输入细分为四个更小的波前片。通过这种方式，我们有效地实现了一种简单但非常快速的自适应波前细分。我们的算法无需使用仅在Shader Model 4.0图形硬件上可用的几何着色器即可运行。

在生成新的波前片列表后，将其传递到波前片更新步骤以推进模拟。这一过程会一直重复，直到模拟体积中不再有波前片。在图6中，我们展示了一个波前通过酒杯传播的情况。计算出的辐照度值被用作颜色，以预览物体周围和内部产生的焦散图案。

图6：（上）玻璃的折射率体积被一个从右侧接近的球面波前探测到。波前的自适应细分也清晰可见。（下）当它穿过物体时，焦散图案出现在其辐照度分布中。

5.3 视图渲染器

基于光源模拟器的输出，我们可以渲染复杂折射物体的任意用户视图。视图渲染器实现了一种快速光线投射器，用于处理任意弯曲的视线，其更新基于方程（11）和（12）。请注意，不需要显式计算光线与表面的交点。沿视线的辐射亮度根据方程（1）计算，使用简化的图像生成模型和存储在输入纹理中的场景参数。

理论上，我们可以处理任意的BRDF模型，包括参数化或表格化的表示形式。然而，由于我们的玻璃物体接近完美反射器，且第一次反射的良好近似在视觉上已经令人满意，因此我们使用简单的动态环境映射。菲涅尔效应和各向异性散射相函数在片段着色器中实时计算。通过空间变化以及与颜色通道相关的衰减，可以逼真地再现彩色物体。可选地，可以添加发射效果，并且如果输入数据包含每个RGB通道的单独折射率字段，则可以模拟色散效应。

在视线完成体积遍历后，我们使用其退出方向在动态环境映射中进行查找，以近似背景辐射亮度。所有光照计算均在高动态范围内完成，并在显示前应用基于[Krawczyk et al. 2005]的自适应色调映射。

6 结果与讨论

图7：使用Persistence of Vision光线追踪器渲染的图像（左）与我们算法渲染的图像（右）的对比。由于折射率场的平滑处理，折射和阴影大小的差异以及略微偏移的焦散图案是伪影。

图8：（左）带有SIGGRAPH标志的玻璃块，具有不同的折射率和吸收率，帧率为15.5fps（场景中有5个物体）。（中）渲染到HDR环境图中的彩色球体，除了其他效果外还展示了轻微的自发光，帧率为26.2fps。（右）玻璃中的复杂折射图案，帧率为13.7fps（场景中有5个物体）。——还请注意玻璃块表面的反射和内部的全反射，以及透过玻璃块可见的圆润立方体。

我们使用五种不同的物体在多种环境中渲染了结果序列，从而展示了不同效果的组合。结果展示在图1和图8中，以及随附的视频中。我们的第一个物体是一个嵌入彩色SIGGRAPH标志的玻璃块。它展示了空间变化的折射和吸收行为，尤其是在标志符号和文字附近（见图8左）。在物体的边界处，可以观察到全反射。另一个有趣的物体是一个由不同吸收特性和变化折射率的玻璃层组成的圆润立方体（见图1右）。它还展示了内部可见的各向异性散射，表现为闪烁。光线在玻璃中的聚焦导致了其内部的体积焦散。类似的效应也可以在渲染到真实世界环境中的玻璃球体上看到（见图8中）。除了所有其他光照效果外，它还具有轻微的自发光成分。我们还展示了一个装有红葡萄酒的玻璃杯（见图1左）。玻璃杯由方向光源照亮，投射出色彩斑斓的焦散到桌面上。它还展示了有趣且复杂的折射效果以及吸引人的表面反射（见图8右）。我们也可以在参与散射的介质中渲染物体。图1（中）展示了一个玻璃兔子，放在充满各向异性散射烟雾的展示柜中。我们调整了吸收参数，使其看起来像是由带有黑色嵌入物的琥珀制成的。它还在其内部各向异性地散射光线。

在视频中，我们首先展示了一个在SIGGRAPH标志后面的移动光源。这是通过将粒子系统渲染到动态环境映射中实现的。这一部分没有进行光照模拟。葡萄酒杯场景展示了我们基于波前的辐照度计算方案的时间行为。辐照度分布是预先计算的。预计算大约花费了90分钟用于600帧。请注意，辐照度分布没有应用时间平滑。在博物馆场景中，我们同时渲染了5个折射物体，并动态更新环境映射。通过这种方式，折射物体可以通过其他折射物体被看到（见图8左）。

为了将我们的算法与真实结果进行比较，我们渲染了一个简单的测试场景（见图7），包括一个平面和一个由方向光源照亮的折射球体。为了这次渲染，我们将环境映射查找替换为片段着色器中的光线-平面交点。使用Hu和Qin [2007]的方法可以准确渲染更复杂的附近几何体。参考解与我们的渲染器之间的差异是体积离散化和梯度计算前折射率场平滑的伪影。

我们的测试数据存储在$128^3$体素体积中。在配备Nvidia GeForce 8800 GTX和768MB视频内存的2.6GHz AMD双核Athlon上，如果显示一个物体且光源保持固定位置，我们能够以800×600像素的分辨率持续获得大约25fps的渲染帧率（见图1左和图8中）。请注意，当非常近距离缩放时，帧率会降低，因为需要从视点向体积中投射更多的光线。还需要注意的是，图1（中和右）以及图8（左和右）的截图是从包含5个折射物体的场景中拍摄的，这些场景需要渲染动态环境映射。因此，这些帧率并不代表渲染单个折射物体的情况。

在将光源移动到新位置后，需要重新运行一次光照模拟。这通常需要大约5到10秒。

对于我们的特定应用，基于ODE的光线传播和自适应波前追踪公式有几个吸引人的优势。体素表示允许快速非线性光线投射。像Purcell等人[2003]中那样昂贵的光线/几何交点计算，会在复杂的弯曲光路径上导致性能瓶颈。自适应波前追踪还使我们能够使用快速粒子追踪器模拟非线性光传输，同时避免欠采样问题。我们在光源位置变化后的更新时间与其他再现较少效果的最先进的GPU方法相当，例如仅在各向同性介质中再现焦散的[Ernst等人2005]。我们认为与光子映射[Jensen 2001]等替代方法相比有优势，因为我们只在需要时插入粒子，即当波前欠采样时。我们在整个三维空间中获得了密集采样的辐照度和方向信息，因此我们可以在场景中的任何点提供各向异性视觉效果。此外，不需要特殊的重建核。此外，我们获得了一个物理上合理的光分布，显著减少了采样问题。与PDE方法相比的优势在于快速模拟，并且能够在光分布多值的情况下选择特定解。对于空间中的特定点，我们选择携带最高能量的光线。如果增加内存消耗和算法复杂性，也可以计算多值解，例如使用多个渲染目标。

尽管在折射物体渲染方面有这些优势，但在一般场景中，我们的算法无法与光子映射等相关方法相媲美，后者可以高效地产生完整的全局光照解决方案。所需的离散化水平使我们的方法仅适用于空间受限的折射物体模拟。这些物体可以通过计算基于网格的物体的标准辐照度衰减，并将我们的预计算体积辐照度值用于进入我们模拟体积的照明表面，作为更大场景的一部分。由于体积表示，场景的大小主要受限于可用的视频内存。八叉树表示可以帮助进一步减少内存消耗。此外，随着未来几代图形卡的发展，内存限制将变得不那么重要。

此外，我们依赖于良好的梯度场来产生视觉上令人愉悦的结果。为此，我们在梯度评估之前对折射率体积进行了预平滑处理。这里需要注意的是，不要过度平滑，否则会导致材料边界周围出现光晕效应。对于极端特写渲染，需要足够高的体素化水平。否则，光照效果中可能会出现离散化伪影。

7 结论

我们提出了一种快速且通用的方法，能够在实时条件下渲染折射物体及其周围的各种复杂光照效果。该方法基于一种复杂的光传输模型，该模型在体积场景表示中考虑了多种效果，包括折射、反射、各向异性散射、发射和吸收。它采用了一种基于Eikonal方程的快速粒子追踪方法，使我们能够在图形硬件上高效地模拟非线性视线和复杂的传播光波前。为了在GPU上实现自适应波前追踪，我们开发了新的数据结构以执行几何细分，这些数据结构甚至可以在Shader Model 4.0之前的架构上运行。

致谢
我们感谢Anders Sundstedt和Michael Schantin在场景建模方面的帮助，以及GusGus允许我们在视频中使用他们的音乐。该项目由Max-Planck视觉计算与通信中心（MPI Informatik/Stanford）支持。

附录

我们推导了几何光学中光线方程的恒定空间步长和恒定时间步长参数化形式。方程（8）是通过结合Eikonal方程：

\[|▽S| = n, \quad (19)\]

和粒子沿波前$S=\text{常数}$的法线运动方程：

\[\frac{dx}{ds} = \frac{▽S}{|▽S|}. \quad (20)\]

得到的。$S$是Eikonal方程的解，该函数的等值面称为波前，它们是从光源出发的等时面。方程（8）的推导可以在[Born and Wolf 1999]中找到。

恒定空间步长参数化

根据方程（20），我们立即有：

\[\left|\frac{dx}{ds}\right|^2 = \frac{dx}{ds} \cdot \frac{dx}{ds} = 1. \quad (21)\]

将方程（19）代入方程（20）得到：

\[n \frac{dx}{ds} = ▽S. \quad (22)\]

设$v = ▽S$，我们得到具有恒定空间步长$ds$的参数化形式，即方程（9）和（10）。

恒定时间步长参数化

我们寻找一种参数化形式，使得：

\[\frac{dS}{dt} = ▽S \cdot \frac{dx}{dt} = 1, \quad (23)\]

即Eikonal函数$S$关于参数$t$的无穷小变化是恒定的。将方程（22）代入方程（23）得到：

\[\frac{1}{n} = \frac{dx}{ds} \cdot \frac{dx}{dt} = \frac{dx}{ds} \cdot \frac{dx}{ds} \frac{ds}{dt} = \frac{ds}{dt}, \quad (24)\]

最后一个等式来源于方程（21）。利用这一结果，我们通过链式法则进行参数变换，从而从方程（9）和（10）得到方程（14）和（15）。