如果有研究水下场景的研究者,可以通过邮箱zhangwenniu@163.com联系我,我目前创建了一个水下场景的研究者交流群,欢迎感兴趣的研究者加入。
链接
论文重点难点讲解
论文重点
- 提出Sea-thru方法
本文提出了一种名为Sea-thru的方法,用于从水下图像中去除水的影响,恢复真实的颜色信息。该方法基于作者之前提出的改进型水下图像形成模型,考虑了信号衰减系数和后向散射系数的非均匀性,以及它们与物体距离和反射率的依赖关系。
- 改进的水下图像形成模型
传统的水下图像形成模型假设散射系数在每个颜色通道中是恒定的,而本文的模型指出:
-
直接信号和后向散射信号由不同的系数控制($\beta_{Dc}$ 和 $\beta_{Bc}$)。
-
这些系数不仅依赖于水的光学特性,还依赖于其他因素,如物体的距离、反射率、环境光谱等。
- 利用RGBD图像进行场景恢复
Sea-thru方法通过RGBD图像(包含颜色和深度信息)来估计后向散射,并利用已知的深度信息和局部空间平均颜色(LSAC)方法估计空间变化的照明,从而获得距离依赖的衰减系数。
- 实验验证
作者使用超过1100张来自两种不同光学水体的图像验证了Sea-thru方法的有效性。结果表明,该方法优于基于传统大气图像形成模型的方法。此外,作者还提供了这些数据集,供其他研究者使用。
- 对水下研究的意义
Sea-thru方法能够一致地去除水的影响,使大规模水下数据集能够更高效地被计算机视觉和机器学习算法处理,为水下探索和保护提供了新的机遇。
论文难点
- 模型复杂性与参数估计
改进的水下图像形成模型引入了更多参数,如距离依赖的衰减系数和后向散射系数。这些参数的估计需要复杂的优化过程,且依赖于已知的深度信息。例如,$\beta_{Dc}(z)$ 的估计需要通过非线性最小二乘拟合来完成。
- 深度信息的获取
为了准确估计衰减系数,需要精确的深度信息。虽然可以通过结构从运动(SfM)或立体成像获取深度图,但这些方法在实际应用中可能存在误差,尤其是在远距离或复杂场景中。
- 后向散射估计的准确性
后向散射的估计依赖于图像中最暗像素的选取,但这些像素可能受到阴影或反射率的影响,导致估计结果不准确。此外,后向散射的估计需要考虑水体类型和环境光的变化。
- 结果评估的挑战
由于水下环境的复杂性,很难获得绝对的“真实”颜色作为基准。虽然作者使用了颜色图表进行定量化评估,但这种方法可能无法完全反映整个场景的恢复效果。
- 模型的普适性
尽管Sea-thru方法在特定数据集上表现出色,但其依赖于改进的图像形成模型和深度信息,可能难以直接应用于其他类型的水下图像或不同的成像条件。
论文详细讲解
论文详细介绍
1. 研究背景
水下图像的颜色恢复是一个具有挑战性的问题。传统的图像形成模型基于大气环境,忽略了水下光的强波长依赖性,导致水下图像颜色失真。作者提出了一个改进的水下图像形成模型,指出:
-
直接信号和后向散射信号由不同的系数控制($\beta_{Dc}$ 和 $\beta_{Bc}$)。
-
这些系数不仅依赖于水的光学特性,还依赖于物体的距离、反射率等因素。
2. 研究方法
本文提出了一种名为 Sea-thru 的方法,用于从水下图像中去除水的影响并恢复真实颜色。该方法基于改进的水下图像形成模型,并利用RGBD图像(包含颜色和深度信息)进行场景恢复。
2.1 水下图像形成模型
水下图像形成模型可以表示为:
\[I_c = D_c + B_c\]其中,$I_c$ 是相机捕获的图像,$D_c$ 是包含场景信息的直接信号,$B_c$ 是由水中悬浮颗粒引起的后向散射信号。直接信号和后向散射信号分别由不同的系数控制:
\[I_c = J_c e^{-\beta_{Dc}(v_D) \cdot z} + B^\infty_c \left(1 - e^{-\beta_{Bc}(v_B) \cdot z}\right)\]其中,$z$ 是相机与场景之间的距离,$J_c$ 是未衰减的场景,$B^\infty_c$ 是背景光。
2.2 Sea-thru方法
Sea-thru方法的核心是估计后向散射和距离依赖的衰减系数。具体步骤如下:
2.2.1 深度信息获取
深度信息通过结构从运动(SfM)技术获取,必要时通过放置已知尺寸的物体进行标定。
2.2.2 后向散射估计
后向散射的估计基于图像中最暗像素,这些像素通常对应于场景中的阴影区域。通过非线性最小二乘拟合,估计后向散射的参数:
\[\hat{B}_c = B^\infty_c \left(1 - e^{-\beta_{Bc} z}\right) + J'_c e^{-\beta'_{Dc} z}\]其中,$J’c e^{-\beta’{Dc} z}$ 是一个残差项,用于修正非完全黑暗的像素。
2.2.3 衰减系数估计
衰减系数 $\beta_{Dc}$ 与距离 $z$ 的关系被建模为双指数函数:
\[\beta_{Dc}(z) = a \cdot e^{b \cdot z} + c \cdot e^{d \cdot z}\]通过局部空间平均颜色(LSAC)方法估计局部照明,并结合深度信息优化衰减系数的估计。
2.3 颜色恢复
通过估计的衰减系数和后向散射,恢复场景颜色:
\[J_c = D_c e^{\beta_{Dc}(z) \cdot z}\]最终,通过全局白平衡调整,获得与水面图像一致的颜色。
3. 实验与结果
作者使用超过1100张来自两种不同光学水体的RGBD图像验证了Sea-thru方法,并与其他方法进行了比较。实验结果表明,Sea-thru在颜色恢复方面优于基于传统大气图像形成模型的方法。具体结果如下:
-
简单对比度拉伸(S1):在距离变化较小的场景中效果较好。
-
基于暗通道先验的方法(S2):通常高估后向散射,导致颜色失真。
-
传统模型(S3):假设 $\beta_{Dc} = \beta_{Bc}$,在距离变化较大的场景中失败。
-
改进模型(S4):不显式计算 $\beta_{Dc}(z)$,在颜色图表上表现较好,但在复杂场景中不如Sea-thru。
-
Sea-thru(S5):利用改进模型和深度信息,表现出最佳的整体恢复效果。
4. 结论
Sea-thru方法通过改进的水下图像形成模型和深度信息,成功地恢复了水下图像的真实颜色。该方法为大规模水下数据集的分析提供了新的可能性,并为水下研究提供了有力的工具。
论文方法部分详解
4. The Sea-thru Method
4.1 Imaging and Range Map Generation
为了恢复水下图像的颜色,需要获取场景的深度信息。Sea-thru方法通过结构从运动(Structure-from-Motion, SFM)技术生成深度图,该技术常用于水下场景的结构复杂性测量。SFM生成的深度图仅提供相对深度,因此需要在场景中放置已知尺寸的物体来标定绝对深度。此外,也可以使用水下机器人导航传感器或立体成像技术获取深度信息。
4.2 Scene Reconstruction
基于水下图像形成模型:
\[I_c = D_c + B_c\]其中,$I_c$ 是相机捕获的图像,$D_c$ 是直接信号,包含场景信息;$B_c$ 是后向散射信号,会随着距离增加而增强。为了恢复未衰减的场景 $J_c$,需要估计直接信号 $D_c$ 和衰减系数 $\beta_{Dc}$:
\[J_c = D_c e^{\beta_{Dc}(z) \cdot z}\]其中,$z$ 是相机与场景之间的距离。为了进一步修正全局光照变化,需要对恢复的场景 $J_c$ 进行白平衡处理:
\[J_s = \frac{J_c}{W_c}\]其中,$W_c$ 是环境光在相机位置的白点。
4.3 Backscatter Estimation
后向散射 $B_c$ 随着距离 $z$ 增加而指数增长,并最终饱和。在场景反射率 $\rho_c \to 0$(完全吸收)或环境光 $E \to 0$(完全阴影)时,图像强度 $I_c \to B_c$。Sea-thru方法通过寻找图像中最暗的RGB三元组来估计后向散射,类似于暗通道先验(DCP),但利用了已知的深度信息。具体步骤如下:
-
将深度图划分为10个均匀的深度簇。
-
在每个深度簇中,找到图像强度最低的1%的RGB三元组,记为 $\mathcal{M}$。
-
使用非线性最小二乘拟合估计后向散射参数:
其中,$J’c e^{-\beta’{Dc} z}$ 是一个残差项,用于修正非完全黑暗的像素。
4.4 Attenuation Coefficient Estimation
4.4.1 $\beta_{Dc}$ as a Function of $z$
衰减系数 $\beta_{Dc}$ 随距离 $z$ 的变化关系被建模为双指数函数:
\[\beta_{Dc}(z) = a \cdot e^{b \cdot z} + c \cdot e^{d \cdot z}\]该模型基于实验数据和理论分析,表明 $\beta_{Dc}$ 随距离的增加而衰减。
4.4.2 Coarse Estimate of $\beta_{Dc}(z)$ From an Image
假设后向散射 $B_c$ 已被去除,直接信号 $D_c$ 可以用来估计衰减系数 $\beta_{Dc}(z)$。通过局部空间平均颜色(LSAC)方法估计局部照明:
\[\hat{\beta}_{Dc}(z) = -\frac{\log \hat{E}_c(z)}{z}\]其中,$\hat{E}_c(z)$ 是通过LSAC方法估计的局部照明,计算公式为:
\[a'_c(x, y) = \frac{1}{N_e} \sum_{(x', y') \in N_e} a_c(x', y')\] \[a_c(x, y) = D_c(x, y) \cdot p + a'_c(x, y) \cdot (1 - p)\]其中,$N_e$ 是以像素 $(x, y)$ 为中心的邻域,$p$ 是控制局部平均范围的参数。
4.4.3 Refined Estimate of $\beta_{Dc}(z)$
利用已知的深度图 $z$,对粗略估计的 $\beta_{Dc}(z)$ 进行优化,使其符合双指数模型:
\[\min_{\beta_{Dc}(z)} \|z - \hat{z}\|\]其中,$\hat{z} = -\frac{\log \hat{E}c}{\beta{Dc}(z)}$。最终,通过优化后的 $\beta_{Dc}(z)$ 恢复场景 $J_c$,并使用灰世界假设或空间域方法进行全局白平衡调整。
4.5 Photo-finishing
使用相机管线操作平台将Sea-thru的输出转换为标准颜色空间,确保输出图像的颜色一致性。
原文翻译

图1. Sea-thru方法从水下图像中去除水的影响。在线查看以获得最佳的颜色和细节效果。
摘要
在水下图像中恢复丢失的颜色仍然是一个具有挑战性的问题。我们最近的研究表明,这在一定程度上是由于广泛使用了适用于大气环境的图像形成模型来处理水下图像,因此我们提出了一种更符合物理规律的模型。改进后的模型表明:
1) 信号的衰减系数在场景中不是均匀的,而是依赖于物体的距离和反射率;
2) 控制后向散射随距离增加的系数与信号衰减系数不同。
在此,我们提出了第一种使用改进模型恢复颜色的方法,该方法利用RGBD图像。Sea-thru方法通过已知深度信息的暗像素估计后向散射,然后利用空间变化的光照估计获得距离依赖的衰减系数。我们使用了来自两种不同光学水体的1100多张图像(这些数据集可供使用),证明了我们的方法优于使用大气模型的方法。一致地去除水的影响将使大规模水下数据集能够被强大的计算机视觉和机器学习算法处理,为未来的水下探索和保护创造了令人兴奋的机会。
1 引言
重建水下图像的颜色是一项艰巨的任务,目前尚无稳健的算法存在。我们最近的研究表明,常用的图像形成模型负有部分责任[1],因为它最初是为大气环境设计的[48],忽略了水下光的强波长依赖性。我们提出了一个改进的模型,表明:
1) 直接信号和后向散射信号由不同的系数控制(旧模型假设它们相同);
2) 这些系数不仅依赖于水的光学特性,还依赖于其他因素(旧模型忽略了这些因素)。
尽管改进的模型在物理上更为准确,但它引入了额外的参数,使得其应用变得困难。在此,我们提出了Sea-thru方法,详细说明了如何估计这些参数以更好地恢复场景。
像ImageNet[20]这样的大规模图像数据集在过去二十年中推动了人工智能的发展,并促成了科学和工业领域的许多重要发现[39]。然而,水下领域虽然拥有大量的图像数据集,但并未充分享受到计算机视觉和机器学习方法带来的便利,部分原因是水掩盖了许多对计算有价值的场景特征。一张水下照片相当于一张在空气中拍摄的照片,但被厚厚的彩色雾覆盖,其白点和强度随距离变化。由于校准过的水下数据集成本高昂且难以获取,为全球海洋的不同光学条件训练基于学习的方法非常困难。现有的尝试逆转水的退化效应的方法要么不稳定,要么过于敏感,要么仅适用于短距离的物体。因此,分析大规模水下数据集通常需要昂贵的手动工作。平均而言,人类专家需要花费超过2小时来识别和计数一小时视频中的鱼类[59]。Sea-thru方法旨在一致地从水下图像中去除水的影响,从而提高大规模数据集的分析效率。其工作原理如下:给定一张RGBD图像,它通过一种受暗通道先验(DCP)启发的方法估计后向散射[34],但利用了已知的深度图。接下来,它使用优化框架,通过局部空间平均颜色[23]获得的光照图作为输入,估计距离依赖的衰减系数。我们证明,距离依赖的衰减系数可以建模为双指数形式,这大大减少了优化步骤中的未知数。我们提供了在两种不同光学水体中获取的1100多张图像(可在http://csms.haifa.ac.il/profiles/tTreibitz/datasets/sea_thru/index.html获取)。在这些图像以及由[7]提供的另一个水下RGBD数据集上,我们定性和定量地证明了Sea-thru——首个利用改进图像形成模型的方法——优于使用旧模型的其他方法。
2 相关工作
恶劣天气下的图像形成模型由Nayar和Narasimhan开发[48]。该模型假设在每个颜色通道中,相机灵敏度范围内的散射系数是恒定的,从而得到每个波长的系数。这一模型后来被广泛用于恶劣天气,并被改编用于水下环境[52]。对于场景恢复,这些方法需要多帧图像或额外信息,例如3D结构。该模型进一步简化为仅包含一个衰减系数,且在所有颜色通道中均匀分布。这种简化是为了实现从单张图像中恢复雾天场景[8][26][33][57],并且后来也被用于水下恢复[17][19][21][44][49]。虽然在水下场景中为所有颜色通道使用相同的系数是一种非常粗糙的近似[1],但为每个通道使用单独的系数可以得到不错的结果[9][13][52][56][58]。然而,正如我们进一步展示的那样,它们的精度本质上受到模型的限制。
后向散射曾通过单张图像使用暗通道先验(DCP)[33]、其一些变体[17][19][21][44]或其他先验[9][49]进行估计。衰减系数可以通过海洋光学仪器(如透射仪或光谱仪)测量[11]。然而,由于光谱灵敏度和接受角的差异,这些仪器的测量结果不能直接用于成像。此外,这些仪器价格昂贵且部署不便。因此,最好直接从图像中估计衰减系数。最基本的方法是在已知距离处拍摄校准目标[60]。在[63]中,系数是从估计的遮蔽光中提取的,忽略了光照颜色。在[9]中,使用灰世界假设估计每个通道的衰减系数。其他方法[19][44][55]通过使用仅针对一种水体测量的固定衰减系数来缓解这一问题。已知距离略微简化了问题,并被用于通过将多张图像的数据拟合到图像形成模型来估计后向散射和衰减[13][51][55]。最近,深度网络被用于重建水下场景[43][53]。然而,它们的训练依赖于完全合成的数据,因此高度依赖于仿真模型的质量。到目前为止,所有方法都假设衰减系数仅是水的属性,并且在每个颜色通道中在场景中是均匀的,但我们已在[1][2]中表明,这是一个错误的假设,会导致重建错误。
3 科学背景
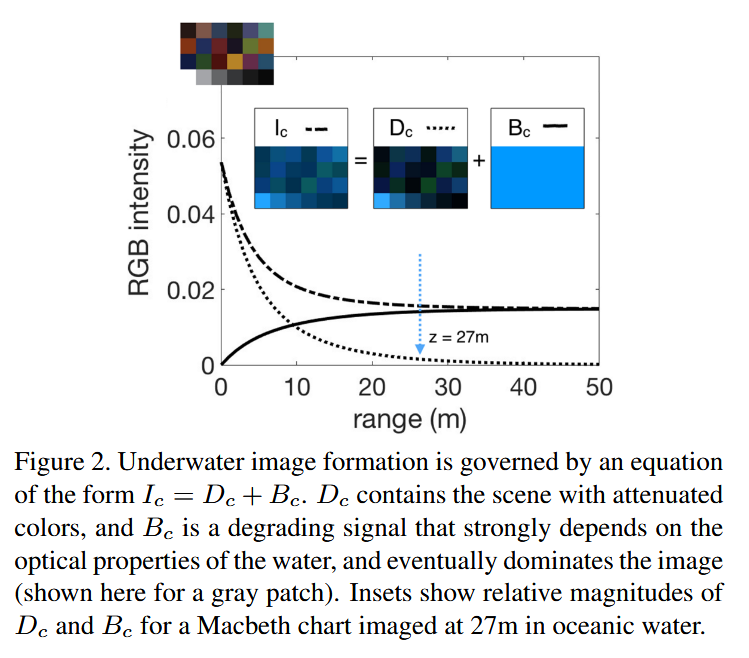
图2. 水下图像形成由公式$I_c = D_c + B_c$控制。$D_c$包含场景的衰减颜色,$B_c$是一种依赖于水的光学特性的退化信号,最终会主导图像(此处以灰色块为例)。插图显示了在海洋水中27米处拍摄的Macbeth色卡的$D_c$和$B_c$的相对幅度。
水下图像的形成遵循以下公式:
\[I_c = D_c + B_c \tag{1}\]其中,$c = \mathrm{R}, \mathrm{G}, \mathrm{B}$ 表示颜色通道,$I_c$ 是相机捕获的图像(颜色失真),$D_c$ 是直接信号,包含关于(衰减后的)场景的信息,$B_c$ 是后向散射,是一种附加信号,由于水体中悬浮颗粒反射的光线而降低图像质量(图2)。分量 $D_c$ 和 $B_c$ 由两个不同的系数 $\beta_c^D$ 和 $\beta_c^B$ 决定,它们分别是宽带(RGB)衰减系数和后向散射系数 [1, 2]。
公式(1)的展开形式如 [1] 所示:
\[I_c = J_ce^{-\beta_c^D(\mathbf{v}_D)\cdot z} + B_c^\infty \left(1 - e^{-\beta_c^B(\mathbf{v}_B)\cdot z} \right) \tag{2}\]其中,$z$ 是相机与场景中沿视线方向的物体之间的距离,$B_c^\infty$ 是散射光,$J_c$ 是在没有沿 $z$ 方向衰减的情况下,在相机位置本应捕获到的未衰减场景。向量 $\mathbf{v}_D = {z,\rho,E,S_c,\beta}$ 和 $\mathbf{v}_B = {E,S_c,b,\beta}$ 表示系数 $\beta_c^D$ 和 $\beta_c^B$ 对距离 $z$、反射率 $\rho$、环境光光谱 $E$、相机光谱响应 $S_c$ 以及水体的物理散射和光束衰减系数 $b$ 和 $\beta$ 的依赖性,所有这些都是波长 $\lambda$ 的函数。此前,人们假设 $\beta_c^D = \beta_c^B$,并且对于给定场景这些系数具有单一值 [9],但在 [1] 中我们已表明它们是不同的,而且它们对不同因素存在依赖性。公式(2) 是为水平方向的成像而推导的。然而,在本研究中,我们将其应用于不同方向捕获的场景,并假设偏差较小。未来的工作应该测试公式(2) 对不同成像方向的适用性。
将RGB系数 $\beta_c^D$ 和 $\beta_c^B$ 与波长相关的物理量联系起来的公式如 [1] 所示:
\[\beta_c^D = \ln \left[ \frac{\int_{\lambda_1}^{\lambda_2} S_c(\lambda)\rho(\lambda)E(d,\lambda)e^{-\beta(\lambda)z}d\lambda}{\int_{\lambda_1}^{\lambda_2} S_c(\lambda)\rho(\lambda)E(d,\lambda)e^{-\beta(\lambda)(z + \Delta z)}d\lambda} \right] / \Delta z, \tag{3}\] \[\beta_c^B = -\ln \left[ 1 - \frac{\int_{\lambda_1}^{\lambda_2} S_c(\lambda)B^{\infty}(\lambda)(1 - e^{-\beta(\lambda)z})d\lambda}{\int_{\lambda_1}^{\lambda_2} B^{\infty}(\lambda)S_c(\lambda)d\lambda} \right] / z. \tag{4}\]这里,$\lambda_1$ 和 $\lambda_2$ 是可见光范围的边界(400和700纳米),$E$ 是深度为 $d$ 处的环境光光谱。垂直穿透的光根据漫射下行衰减 $K_d(\lambda)$ 进行衰减 [47],这与光束衰减系数 $\beta(\lambda)$ 不同 [1, 47],光束衰减系数 $\beta(\lambda)$ 仅仅是海洋中溶解物质的类型、成分和密度的函数 [47]。如果 $E(0,\lambda)$ 是海面的光,那么深度 $d$ 处的 $E(d,\lambda)$ 如 [2] 所示:
\[E(d,\lambda) = E(0,\lambda)e^{-K_d(\lambda)d}. \tag{5}\]公式(2) 中的散射光 $B_c^{\infty}$ 表示为:
\[B_c^{\infty} = \int_{\lambda_1}^{\lambda_2} S_c(\lambda)B^{\infty}(\lambda)d\lambda, \tag{6}\]其中
\[B^{\infty}(\lambda) = [b(\lambda)E(d,\lambda)] / \beta(\lambda). \tag{7}\]4 Sea - thru方法
基于公式(2 - 4),要恢复 $J_c$ ,需要知道或估计以下参数:由 $b$、$\beta$ 和 $K_d$ 确定的光学水类型;光线 $E_d$ 、相机与场景沿视线方向的距离 $z$ 、拍摄照片时的深度 $d$ 、场景中每个物体的反射率 $\rho$ 以及相机的光谱响应 $S_c$ 。在拍摄水下照片时,这些参数很少(如果有的话)是已知的。在 [1] 中我们表明,$\beta_c^D$ 主要受 $z$ 的影响,而 $\beta_c^B$ 主要受光学水类型和光照 $E$ 的影响。因此,我们调整了Sea - thru方法来处理这些特定的依赖关系。由于这些系数会随着成像角度和曝光而变化 [1],我们假设一般情况下它们不能跨图像传递,即使是用同一台相机连续拍摄的图像也是如此,并且我们仅从给定的图像中估计相关参数。
4.1 成像和距离图生成

图3. (a) 使用Photoscan Professional(Agisoft LLC)从68张照片创建的3D模型。
(b) 图1中图像的深度图$z$(单位:米),由该模型生成。我们在海底放置了一个色卡以设置比例。
由于 $\beta_c^D$ 严重依赖于 $z$ ,我们需要有场景的距离图,我们使用运动恢复结构(SFM)来获取,该方法在水下常用于测量珊瑚礁的结构复杂性(例如 [12, 15, 16, 27, 28, 42])以及在考古学中应用(例如 [45, 46])。我们的方法需要 $z$ 的绝对值,而SFM 只能提供按比例的距离,所以我们在场景中放置已知尺寸的物体(图3)。当从水下航行器进行成像时,其导航传感器可以提供速度或高度信息。另一种方法是立体成像(例如 [7, 9, 35, 54]),这需要使用两个同步相机,并且在成像调查开始前进行简单的水下校准。
4.2 场景重建
从公式(1)和(2)我们可得:
\[J_c = D_ce^{\beta_c^D(z)z} \tag{8}\]其中 $D_c = I_c - B_c$ 。这里我们明确保留了 $\beta_c^D$ 对 $z$ 的依赖性,因为我们必须考虑这一因素,但我们将忽略其他的依赖关系。$J_c$ 是一幅其颜色仅沿 $z$ 方向校正过的图像,并且根据成像几何关系,可能需要进一步校正才能得到在海面拍摄的图像的颜色。设 $J_s$ 表示在海面拍摄的图像。那么,
\[J_s = J_c/W_c \tag{9}\]其中 $W_c$ 是相机所在位置(即深度 $d$ 处)环境光的白点,$J_s$ 是经过全局白平衡处理的 $J_c$ 。
4.3 后向散射估计
后向散射随 $z$ 呈指数增长,最终达到饱和(图2)。当场景反射率 $\rho_c \to 0$(所有光线被吸收),或 $E \to 0$(完全处于阴影中)时,捕获的RGB强度 $I_c \to B_c$ 。我们在图像中搜索非常暗或处于阴影中的像素,并利用它们来得到后向散射的初始估计值。我们的方法与暗通道先验(DCP)相似,都是试图在 $D_c$ 最小的地方找到后向散射信号,但根本区别在于我们利用已知的距离图,而不是尝试去估计它。此外,我们搜索最暗的RGB三通道像素值组合,而不是在每个颜色通道中独立寻找最暗的像素,并且我们不生成暗通道图像。我们的方法识别出的少量不相连像素就足够了,因为我们有相应的距离信息,以及 $B_c$ 随 $z$ 变化的物理模型(但请参阅第3节中关于成像角度的注释)。
我们按如下方式估计后向散射:首先,我们将距离图划分为10个等间距的簇,覆盖 $z$ 的最小值和最大值。在每个距离簇中,我们在 $I_c$ 中搜索处于后1% 的RGB三通道像素值组合,我们用 $\Omega$ 表示。然后在整个图像中,$\hat{B}_c(\Omega) \approx I_c(\Omega)$ 是对后向散射的一个高估,我们将其建模为:
\[\hat{B}_c = B_c^{\infty}(1 - e^{-\beta_c^B z}) + J_c'e^{-\beta_c^{D'} z} \tag{10}\]其中表达式 $J_c’e^{-\beta_c^{D’} z}$ 表示一个类似直接信号的小残差项。使用非线性最小二乘拟合,我们在边界 $[0, 1]$、$[0, 5]$、$[0, 1]$ 和 $[0, 5]$ 内分别估计参数 $B_c^{\infty}$、$\beta_c^B$、$J_c’$ 和 $\beta_c^{D’}$ 。在这一步中,我们忽略 $\beta_c^{D’}$ 对 $z$ 的依赖性。如果关于相机传感器、水类型等的信息可用,$\beta_c^D$ 和 $\beta_c^B$ 的边界可以使用 [1, 2] 中描述的轨迹进一步细化。
根据场景不同,如果找到的暗像素的反射率为纯黑色、暗像素处于阴影中、$z$ 较大,或者水极其浑浊($B_c \gg D_c$),公式(10) 中的残差项可以忽略。在其他所有情况下,包含残差项是很重要的。在珊瑚礁场景中,由于其复杂的三维结构,通常有许多处于阴影中的像素,这些像素可以直接用来估计后向散射。
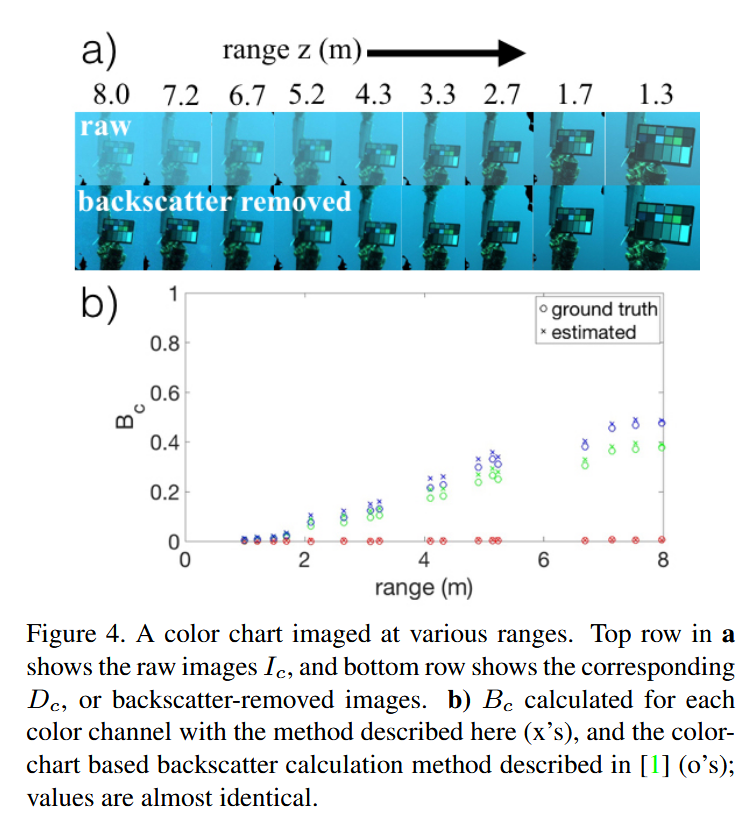
图4. 在不同距离处拍摄的色卡。
(a) 顶部行显示原始图像$I_c$,底部行显示对应的$D_c$,即去除后向散射后的图像。
(b) 使用本文描述的方法计算的每个颜色通道的$B_c$(用“x”表示),以及[1]中描述的基于色卡的后向散射计算方法(用“o”表示);两者数值几乎相同。
图4展示了该方法在经过校准的实验中的性能表现。我们在蓝色海水中的浮标线处放置了一张色卡(以尽量减少来自海底和海面的相互反射),并在向其游近的过程中进行拍摄。后向散射的散射效应在远处拍摄的图像中清晰可见,并且随着相机与色卡之间的距离 $z$ 减小而减弱(图4a)。对于每一张图像,我们按照 [1] 中所述,使用色卡的消色差色块来计算真实的后向散射值,同时也使用这里描述的方法进行估计(图4b)。得到的 $B_c$ 值几乎相同;除了 $I_c$ 和 $z$ 之外,不需要其他输入(例如水的类型)就能得到这个结果。需要注意的是,在任何一张图像中,色卡的黑色色块都没有被纳入 $\Omega$ 中,这表明它实际上只是深灰色,比真正的黑色或处于阴影中的像素要亮得多。
4.4 衰减系数估计
4.4.1 $\beta_c^D$ 作为 $z$ 的函数
我们之前的研究表明,$\beta_c^D$ 与距离 $z$ 的相关性最强 [1, 2]。观察公式(3) 可知,这种变化呈指数衰减形式。在描述如何从图像中提取 $\beta_c^D(z)$ 之前,我们先建立 $\beta_c^D$ 与 $z$ 之间的关系。
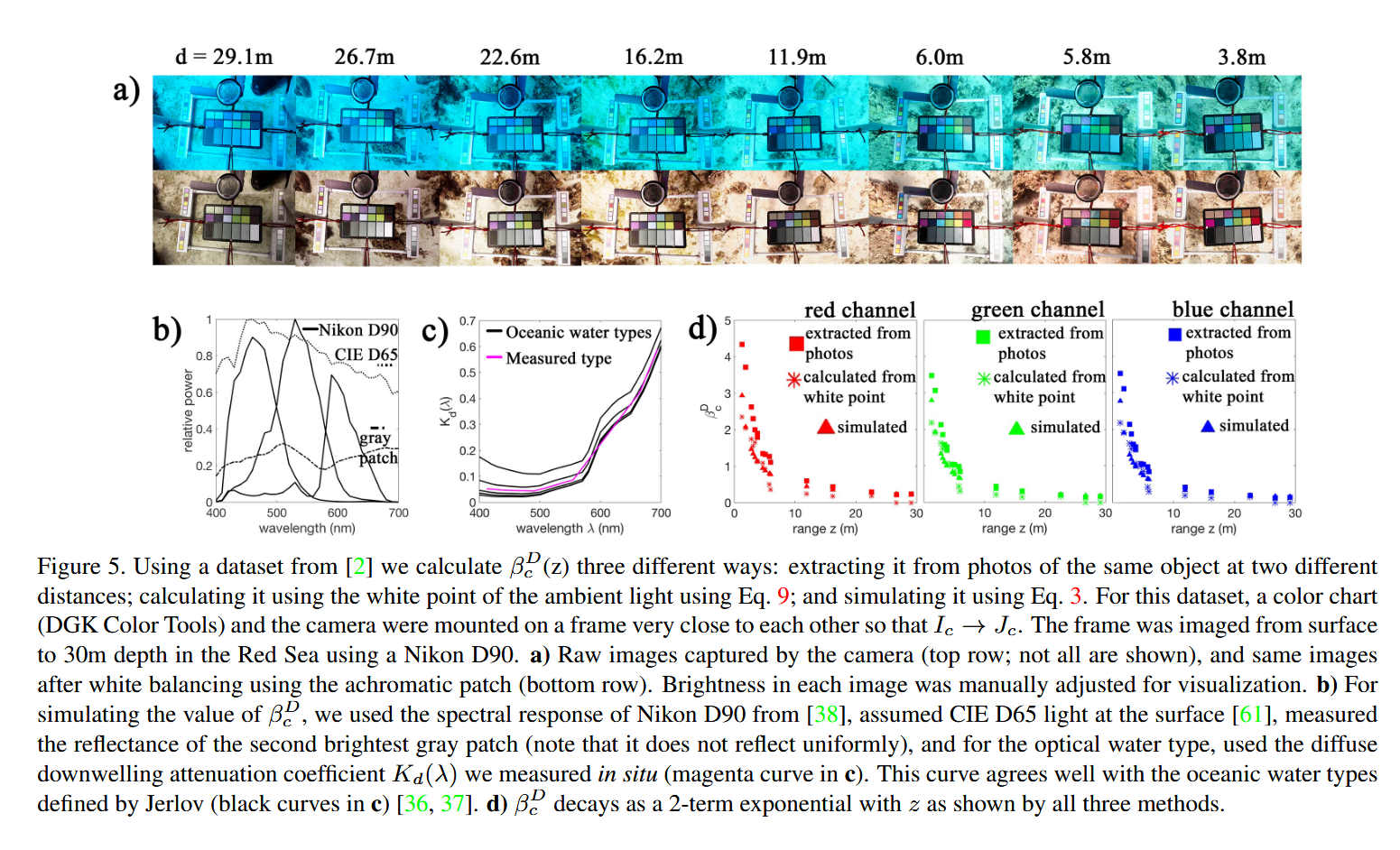
图5. 使用[2]中的数据集,我们通过三种不同方法计算$\beta_{Dc}(z)$:
- 从两个不同距离处拍摄的同一物体照片中提取;
- 使用环境光的白点通过公式(9)计算;
- 使用公式(3)进行模拟。
对于该数据集,色卡(DGK Color Tools)和相机被安装在非常靠近的框架上,使得$I_c \to J_c$。该框架在红海从水面到30米深度处被拍摄,使用的是Nikon D90相机。
(a) 相机捕获的原始图像(顶部行;未显示全部),以及使用中性灰块进行白平衡后的相同图像(底部行)。每张图像的亮度都经过手动调整以便于可视化。
(b) 为了模拟$\beta_{Dc}$的值,我们使用了Nikon D90的光谱响应[38],假设表面为CIE D65光源[61],测量了第二亮的灰色块的反射率(注意它不是均匀反射的),并且对于水体类型,使用了我们现场测量的漫射衰减系数$K_d(\lambda)$(图c中的品红色曲线)。该曲线与Jerlov定义的海洋水体类型(图c中的黑色曲线)[36][37]吻合得很好。
(d) 所有三种方法均表明,$\beta_{Dc}$随$z$呈双指数衰减。
图5展示了 [2] 中的一个实验,我们将一张色卡和一台尼康D90相机安装在一个框架上,两者间距约20厘米,然后将这个装置从海面下放到30米深的地方,同时进行拍摄。由于色卡与相机之间的距离 $z$ 很小,相机和色卡之间的后向散射和衰减都可以忽略不计,因此 $I_c \to J_c$ 。在这个设置中,颜色损失是由于在从海面开始的垂直距离 $d$ 上起作用的有效衰减系数导致的,并且反映在每个深度处环境光的白点 $W_c$ 中。
从每一张图像中,我们通过两种不同的方式计算垂直方向上的有效 $\beta_c^D$:一种是按照 [2] 中所述的成对图像法,另一种是使用公式(9),其中 $W_c$ 是从色卡中第二块(24%)灰色色块的强度中提取的。此外,我们使用公式(3),根据 [38] 中相机的光谱响应,以及我们测量得到的在垂直方向起作用的水体的 $K_d(\lambda)$,来计算该水类型下 $\beta_c^D$ 的理论值。图5中这三种估计 $\beta_c^D$ 的方法都表明,$\beta_c^D$ 随距离衰减,在这种情况下是随深度 $d$ 衰减。基于图5中的数据和额外的模拟,我们用一个两项指数形式来描述 $\beta_c^D$ 对任意距离 $z$ 的依赖关系:
\[\beta_c^D(z) = a * \exp(b * z)+c * \exp(d * z). \tag{11}\]对于短距离,$\beta_c^D(z)$ 也可以建模为一条直线。
4.4.2 从图像中粗略估计 $\beta_c^D(z)$
假设已成功从图像 $I_c$ 中去除 $B_c$,我们现在可以从直接信号 $D_c$ 着手估计 $\beta_c^D(z)$。从公式(2) 可知,直接信号是场景 $J_c$(在相机位置)乘以衰减项 $e^{-\beta_c^D(z)z}$ 的结果。因此,恢复场景 $J_c$ 就简化为估计相机与场景之间的光照图的问题,而该光照图在空间上是变化的。给定局部光照图的估计值 $\hat{E}_c(z)$,我们可以按如下方式得到 $\beta_c^D(z)$ 的估计值:
\[\hat{\beta}_c^D(z)=-\log\hat{E}_c(z)/z. \tag{12}\]在计算颜色恒常性领域中,局部光照估计是一个被深入研究的课题(例如 [6, 10, 22, 29, 32, 41])。一些方法,尤其是模仿人类对不同光照进行补偿能力的Retinex模型,已被应用于水下图像(例如 [30, 62]),并且最近的一项研究表明,大气图像去雾与Retinex之间存在直接的线性关系 [31]。如果能从原始图像中正确去除后向散射,我们可以预期许多多光照估计方法在水下图像上也能很好地发挥作用。在这里,我们采用 [24] 中描述的局部空间平均颜色(LSAC)方法的一种变体,因为它利用了已知的距离图。该方法的工作原理如下:对于颜色通道 $c$ 中的给定像素 $(x,y)$,通过更新以下公式迭代估计局部空间平均颜色 $a_c(x,y)$:
\[a_c'(x,y)=\frac{1}{N_e}\sum_{N_e}a_c(x',y') \tag{13}\] \[a_c(x,y)=D_c(x,y)p + a_c'(x,y)(1 - p), \tag{14}\]其中邻域 $N_e$ 定义为与像素 $(x,y)$ 4 - 连通且与该像素之间的距离小于距离阈值 $\epsilon$ 的像素:
\[N_e(x',y')=(x',y')\text{ with } \|z(x,y)-z(x',y')\|\leq\epsilon. \tag{15}\]这里,对于所有像素,$a(x, y)$ 的初始值设为零,因为经过大量迭代后,初始值的影响将微不足道。参数 $p$ 描述了用于计算平均值的局部支持区域,它取决于图像的大小;$p$ 值较大意味着将在较小的邻域内计算局部空间平均颜色。然后,局部光照图可通过 $\hat{E}_c = fa_c$ 得到,其中 $f$ 是一个基于几何关系的因子,对所有颜色通道进行等比例缩放,并且可以根据所观察的场景确定。根据 [23],当相机与场景呈垂直方向时,我们取 $f = 2$。
4.4.3 $\beta_c^D(z)$ 的精确估计
接下来,我们利用已知的距离图 $z$ ,对通过公式(12 - 15) 得到的 $\beta_c^D(z)$ 的估计值进行优化,使其符合给定的 $z$ 。我们将公式(12) 改写为:
\[\hat{z}=-\log\hat{E}_c/\beta_c^D(z) \tag{16}\]并最小化:
\[\min_{\beta_c^D(z)}\|z - \hat{z}\| \tag{17}\]其中 $\beta_c^D(z)$ 采用公式(11) 的形式,包含参数 $a, b, c, d$ 。为得到衰减的指数形式,这些参数的上下界分别为 $[0, -\infty, 0, -\infty]$ 和 $[\infty, 0, \infty, 0]$ ,但可以利用从公式(12) 得到的粗略估计值来缩小范围。利用优化后的 $\beta_c^D(z)$ 估计值,我们通过公式(8) 恢复 $J_c$ 。在 $J_c$ 中,环境光的空间变化已经得到校正,所以接下来只需估计全局白点 $W_c$ 。这可以使用基于统计或基于学习的方法来完成(相关综述见 [32]);在这里,对于包含足够多样颜色的场景,我们采用简单快速的灰色世界假设 [14] ,而对于单色场景(如我们接下来要介绍的数据集D4),我们使用 [18] 中的一种不依赖颜色信息的空间域方法。
4.5 图像后期处理
我们使用 [40] 中描述的相机流水线操作平台,将Sea - thru方法的输出转换到标准颜色空间,在第6步之前将其插入流水线,并指定一个单位矩阵用于白平衡。
5 数据集
我们提供了五个水下RGB - D数据集(表1)。所有数据集都是在自然光照下以原始格式采集的,对于给定的一组数据,曝光设置保持不变,并且包含多张带有色卡的图像。
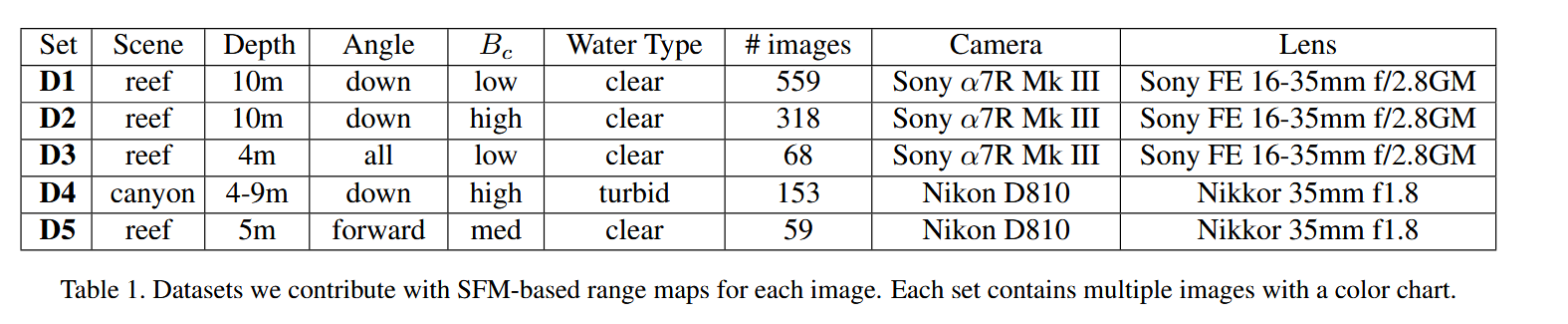
表1. 我们提供的数据集,包含基于SfM的每张图像的深度图。每个数据集包含多个带有色卡的图像。
6 结果:验证和误差分析
我们使用表1中的数据集以及 [7] 中的立体RGB - D数据集来测试以下场景:
S1. 简单对比度拉伸。
S2. 对 $B_c$ 估计不正确的旧模型。具体来说,我们使用暗通道先验(DCP)[34],该方法在水下场景中通常会高估 $B_c$ 。我们使用Matlab中的内置函数 imreducehaze 。
S3. 对 $B_c$ 估计正确的旧模型(即正确估计 $B_c^{\infty}$ 和 $\beta_c^B$ ),并假设 $\beta_c = \beta_c^D = \beta_c^B$ 。
S4. 修正后的模型,对 $B_c$ 估计正确,并且 $J_c$ 通过 $J_c = D_c/\hat{E}_c$ 得到,而不明确计算 $\beta_c^D(z)$ 。
S5. Sea - thru方法,使用修正后的模型,其中 $\beta_c^B \neq \beta_c^D$ ,且 $\beta_c^D$ 采用公式(11) 中的 $\beta_c^D(z)$ 。
由于Sea - thru是首个使用修正后的水下图像形成模型的算法,并且具有距离图这一优势,我们没有将其性能与同样试图估计距离/透射率的单图像颜色重建方法进行对比测试。在对这些方法进行了细致研究后,[7] 的作者发现基于暗通道先验(DCP)的方法 [21, 50] 无法持续地校正颜色,而其他方法 [3, 4, 5, 25] 旨在增强图像,而非实现物理上准确的校正。[7] 中提出的方法确实旨在恢复物理上准确的颜色(使用旧模型),但仅适用于场景中距离足够大的水平成像,这使得它不适用于我们的许多图像。
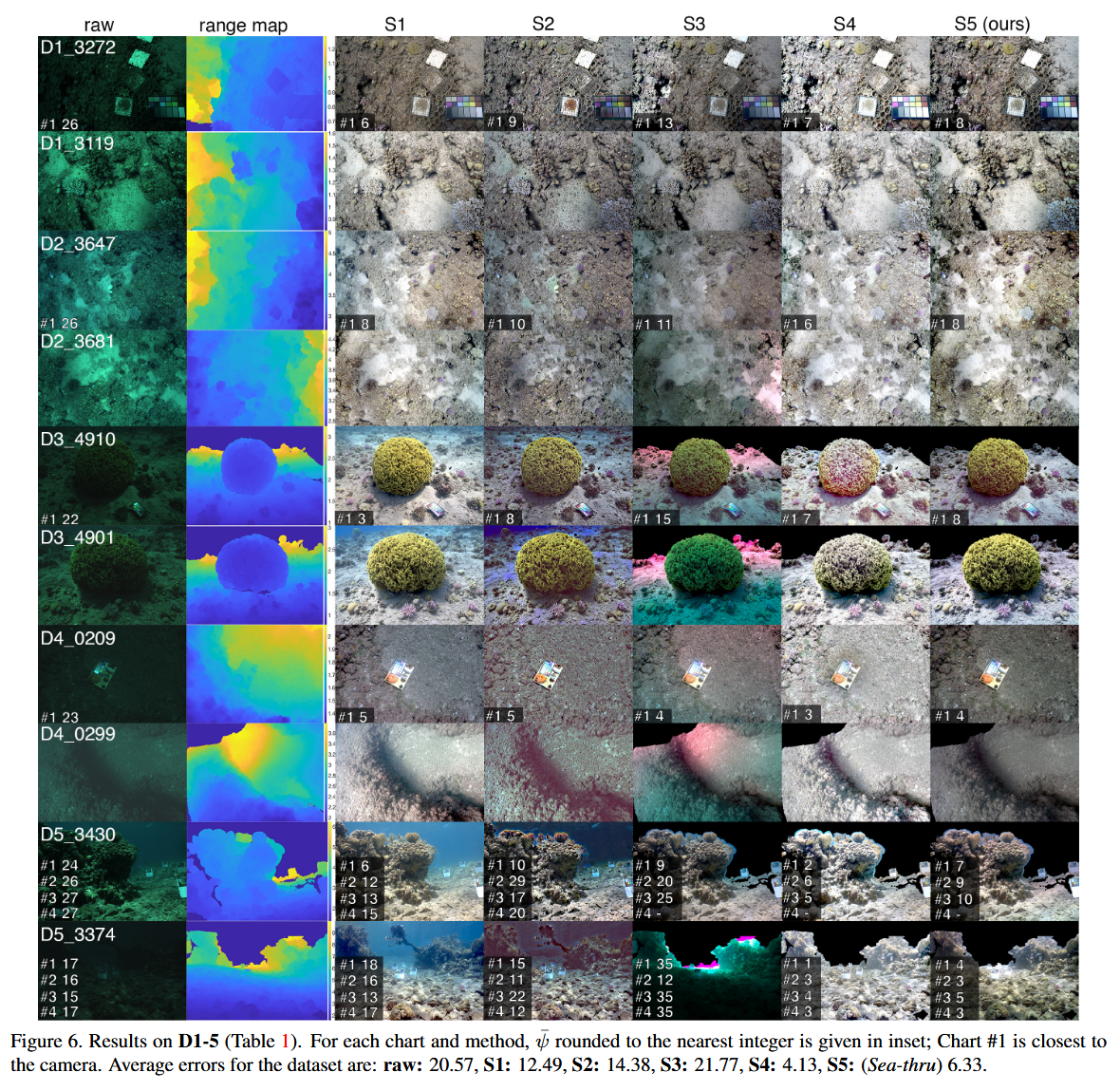
图6. 在D1-5(表1)上的结果。对于每个色卡和方法,平均误差$\bar{\psi}$四舍五入到最近的整数,并在图中显示;色卡#1最靠近相机。数据集的平均误差分别为:原始图像:20.57,S1:12.49,S2:14.38,S3:21.77,S4:4.13,S5(Sea-thru):6.33。
我们在图6中展示了D1 - 5数据集的原始图像、距离图以及对应的S1 - S5结果,在图7中展示了 [7] 中立体数据库的相关内容。为进行评估,我们使用了每个色卡的六个灰度色块与纯灰色之间的RGB角度误差 $\bar{\psi}$ ,并对每个色卡取平均值:
\[\bar{\psi}=(1/6)\cos^{-1}[I_c/(\sqrt{3}\|I_c\|)] \tag{18}\][7] 中也采用了同样的方法。 $\bar{\psi}$ 值越低表示校正效果越好(不过也有例外情况,见下文);以度为单位的误差在图6和图7的插图中针对有色卡的场景列出,结果四舍五入到最接近的整数。

图7. 在[7]中的立体数据集上的结果。其深度图经过进一步处理以去除虚假像素。平均误差$\bar{\psi}$四舍五入到最近的整数,并在图中显示;色卡#1最靠近相机。S1和S2未使用深度图;对于其他方法,缺少$\bar{\psi}$值表示缺少深度信息。所有图像的平均误差分别为:原始图像:22.28,S1:6.83,S2:10.03,S3:12.04,S4:4.46,S5(Sea-thru):4.94。
在所有情况下,全局的简单对比度拉伸方法S1,在场景距离大致均匀时效果良好。DCP方法(S2)通常会高估后向散射(这在一定程度上能提高可见度),但通常会扭曲颜色并产生伪色。例如,在两个数据集中,本应颜色均匀的沙子呈现出绿色和紫色。在D1_3272图像中,S2 中色卡的灰色色块有明显的紫色伪影,但其 $\bar{\psi}$ 误差却低于S5,这表明 $\bar{\psi}$ 并非量化颜色重建误差的最佳指标。在S3 - S5中,都减去了正确量的 $B_c$ 。在S3中,像使用旧模型的方法那样,用恒定的 $\beta_c^D$ 校正衰减。当距离变化较大时(例如图7),恒定 $\beta_c^D$ 假设的缺陷最为明显,而这也是S5具有最大优势的地方(尽管S3在短距离场景中也会失效,例如D3和D4数据集)。距离图在离相机最远的地方往往最不准确,这也增加了在远距离重建颜色的难度。S4有时在色卡上产生的误差比S5低。这是合理的,因为计算色卡上的光照更容易;然而,S5在完整场景上的效果更好。S4可用于一阶校正,效果比以前的方法更好 。
7 结论
Sea-thru方法基于为海洋环境开发的图像形成模型,能够以无偏色的方式揭示水下世界。它强调了$\beta_{Dc}$和$\beta_{Bc}$是不同的,并且$\beta_{Dc}$对距离$z$的依赖性不可忽视。我们专注于恢复$z$依赖性,因为这是最显著的,但未来计划还将恢复反射率$\rho$的依赖性以进一步改进校正。由于恢复这些复杂的依赖性极具挑战性,深度网络的表现可能会优于我们所使用的方法。由于无法为这种环境获取绝对真实值,因此其训练必须基于正确图像形成模型的精心设计的仿真进行。精心设计的仿真还可以帮助解决我们在工作中遇到的另一个挑战——结果评估。在[7]中发布的数据集是通过在场景中放置多个颜色图表的巨大努力获得的,但仅限于图表的评估并不总能说明全部问题。Sea-thru是向强大的计算机视觉和机器学习算法开放大规模水下数据集的重要一步,并将有助于推动水下研究,因为我们的海洋正面临来自污染、过度捕捞和气候变化的日益增加的压力。
8 致谢
本研究得到了The Leona M. and Harry B. Helmsley Charitable Trust、Maurice Hatter基金会、科学技术与空间部资助#3-12487、ISF资助#680/18、Technion Ollendorff Minerva视觉与图像科学中心以及海法大学博士后项目的资助。我们感谢Tom Shlesinger、Deborah Levy、Matan Yuval、Ben Singer、H. Can Karaimer以及埃拉特海洋科学研究所的支持。
评论