k038 An Approximate Image-Space Approach for Interactive Refraction

Zhangwenniu 于 2025-03-07 发布  |   阅读量: 次

链接

论文重点难点详解

论文重点

  1. 提出了一种交互式的图像空间方法用于近似折射：
  1. 基于图像空间的折射计算：
  1. 对复杂几何体的处理：
  1. 性能表现：

论文难点

  1. 对凹形物体的处理：
  1. 全内反射的处理：
  1. 对复杂折射的近似：
  1. 仅支持无限环境贴图：

论文详细讲解

1. 研究背景与动机

在许多交互式应用中，实时性优先于真实感渲染。由于帧率限制，大多数真实感效果需要在图形硬件上高效运行。折射是被广泛忽略的一种效果，因为传统的GPU方法通常只支持通过单个表面的折射。然而，在现实场景中，折射通常涉及多个表面（例如透过眼镜或复杂物体）。因此，本文提出了一种简单且高效的图像空间方法，支持通过两个界面的折射，适用于现代图形硬件。

2. 基础折射原理

折射的基本计算依赖于斯涅尔定律（Snell’s Law）：

\[n_i \sin \theta_i = n_t \sin \theta_t\]

其中，\(n_i\) 和 \(n_t\) 分别是入射介质和透射介质的折射率，\(\theta_i\) 是入射光线与表面法线的夹角，\(\theta_t\) 是折射光线与法线的夹角。在光线追踪中，折射光线可以独立地与几何体相交，并递归应用斯涅尔定律。然而，在GPU的流式处理中，逐像素独立操作成本较高，因此需要一种近似方法。

3. 图像空间折射方法

本文提出了一种基于图像空间的折射近似方法，通过两次GPU遍历来实现。核心思想是利用光栅化后的信息（入射方向、击中点、表面法线等）来近似计算两次折射。

3.1 近似第二个折射点 \(P_2\)

为了计算第二次折射，需要知道折射光线的方向 \(\vec{T}_1\)、第二个折射点 \(P_2\) 和该点的法线 \(\vec{N}_2\)。其中，\(\vec{T}_1\) 可以通过斯涅尔定律计算，而 \(P_2\) 和 \(\vec{N}_2\) 的计算较为复杂。本文提出了一种近似方法：

  1. 假设 \(P_2 = P_1 + d \vec{T}_1\)，其中 \(d\) 是 \(P_1\) 和 \(P_2\) 之间的距离。

  2. 近似计算 \(d\)：通过渲染几何体的前后表面，分别存储深度缓冲区，从而计算出前后表面之间的距离 \(d_{\vec{V}}\) 和沿法线方向的距离 \(d_{\vec{N}}\)。

  3. 使用插值方法计算近似距离 \(\tilde{d}\)：

\[\tilde{d} = \frac{\theta_t}{\theta_i} d_{\vec{V}} + \left(1 - \frac{\theta_t}{\theta_i}\right) d_{\vec{N}}\]

从而得到近似的第二个折射点 \(\tilde{P}_2 = P_1 + \tilde{d} \vec{T}_1\)。

3.2 确定法线 \(\vec{N}_2\)

确定 \(\vec{N}_2\) 的关键在于找到 \(\vec{T}_1\) 与几何体相交的多边形。对于凸形物体，可以通过两次光栅化（一次剔除前表面，一次剔除后表面）来实现：

  1. 在第一次遍历中，将后表面的法线存储到纹理中。

  2. 在第二次遍历中，将近似的点 \(\tilde{P}_2\) 投影到纹理空间，通过纹理查找获取法线 \(\vec{N}_2\)。

对于凹形物体，可以选择最远表面或第二个表面作为二次折射的参考。这两种方法各有优缺点：最远表面更符合用户期望，而第二个表面可以避免深度复杂度较高的问题。

3.3 问题与限制

该方法存在以下问题：

  1. 全内反射（TIR）：无法直接处理全内反射，通过限制入射角避免该问题。

  2. 投影错误：当 \(\tilde{P}_2\) 投影到错误的多边形上时，会导致错误的折射结果。

  3. 深度复杂度：对于深度复杂度较高的凹形物体，近似方法可能导致明显的误差。

  4. 仅支持无限环境贴图：当前方法无法实现物体之间的折射。

4. 实验结果

实验在 NVIDIA GeForce 6800 GPU 上实现，使用 OpenGL 和 Cg 着色器。实验结果表明，该方法能够在复杂模型上实现高帧率的交互式渲染。例如：

5. 结论与未来工作

本文提出了一种简单且高效的图像空间方法，能够在现代GPU上实现通过两个界面的交互式折射。该方法适用于复杂模型，但存在一些限制，例如仅支持无限环境贴图，无法处理物体之间的折射。未来的工作将致力于解决这些问题，并探索如何更好地处理凹形物体以及将该方法应用于快速生成焦散效果。

论文方法详解

3. 图像空间折射方法

本文提出了一种基于图像空间的折射近似方法，能够在GPU上高效实现通过两个界面的折射效果。该方法的核心在于利用光栅化后的信息，通过两次GPU遍历来近似计算折射路径。

3.1 近似第二个折射点 \(P_2\)

为了计算第二次折射，需要确定第二个折射点 \(P_2\) 和该点的法线 \(\vec{N}_2\)。由于直接计算 \(P_2\) 需要逐像素射线追踪，成本较高，因此本文采用一种近似方法：

  1. 参数化光线：假设光线从点 \(P_1\) 出发，方向为 \(\vec{T}_1\)，则 \(P_2\) 可以表示为：
\[P_2 = P_1 + d \vec{T}_1\]

其中，\(d\) 是 \(P_1\) 和 \(P_2\) 之间的距离。

  1. 近似距离 \(d\)：
\[\tilde{d} = \frac{\theta_t}{\theta_i} d_{\vec{V}} + \left(1 - \frac{\theta_t}{\theta_i}\right) d_{\vec{N}}\]

其中，\(\theta_i\) 和 \(\theta_t\) 分别是入射角和折射角。

  1. 近似点 \(\tilde{P}_2\)：
\[\tilde{P}_2 = P_1 + \tilde{d} \vec{T}_1\]

通过这种方式，可以在不进行射线追踪的情况下近似计算第二个折射点。

3.2 确定法线 \(\vec{N}_2\)

确定法线 \(\vec{N}_2\) 的关键在于找到 \(\vec{T}_1\) 与几何体相交的多边形。本文通过图像空间方法实现：

  1. 两次光栅化：
  1. 处理凹形物体：

3.3 问题与限制

尽管该方法能够在GPU上高效实现折射效果，但仍存在一些问题和限制：

  1. 全内反射（TIR）：
  1. 投影错误：
  1. 深度复杂度：
  1. 仅支持无限环境贴图：

总结

本文提出的方法通过两次GPU遍历，利用图像空间信息近似计算两次折射，能够在现代图形硬件上高效运行。尽管存在一些限制，但该方法为交互式折射渲染提供了一种实用的解决方案，适用于复杂模型和场景。

重点问题讲解

光栅化（Rasterization）

光栅化（Rasterization）是计算机图形学中一个核心的概念，指的是将几何图形数据（如点、线、多边形等）转换为光栅图像（即像素数组）的过程。简单来说，光栅化就是把矢量图形转换为像素图像的过程。它是现代图形渲染管线中的一个重要环节，广泛应用于实时渲染和计算机图形学的各个领域。

光栅化的具体过程

光栅化通常涉及以下几个关键步骤：

  1. 顶点处理（Vertex Processing）：
  1. 图元装配（Primitive Assembly）：
  1. 光栅化（Rasterization）：
  1. 片段处理（Fragment Processing）：
  1. 像素操作（Pixel Operations）：

光栅化的优点

  1. 高效性：
  1. 硬件支持：
  1. 灵活性：

光栅化的局限性

  1. 无法直接处理全局光照：
  1. 依赖几何表示：

总结

光栅化是计算机图形学中一种重要的渲染技术，广泛应用于实时渲染领域。它通过将几何图形转换为像素图像，实现了高效的图形渲染。尽管存在一些局限性，但光栅化仍然是现代图形硬件和实时渲染系统的核心技术之一。

矢量图形

矢量图形（Vector Graphics）是一种使用几何形状（如点、线、曲线、多边形等）来表示图像的图形格式。与位图图像（由像素组成的图像）不同，矢量图形通过数学方程和几何元素的集合来描述图像的内容，因此具有可缩放、无损放大和高分辨率显示的特点。

矢量图形的主要特点

  1. 基于几何元素：
  1. 分辨率无关性：
  1. 文件大小较小：
  1. 可编辑性高：

矢量图形的应用

  1. 图形设计：
  1. 网页设计：
  1. 动画制作：
  1. 科学和工程绘图：

矢量图形与位图图像的区别

特性 矢量图形 位图图像
数据表示 几何形状和数学公式 像素数组
缩放效果 无损缩放，始终保持清晰 放大时可能出现像素化，模糊不清
文件大小 通常较小 通常较大，取决于分辨率和颜色深度
编辑性 高，可直接编辑几何形状 低，编辑像素较为复杂
适用场景 标志、排版、网页设计、动画 照片、数字绘画、复杂纹理

矢量图形的常见格式

  1. SVG（Scalable Vector Graphics）：
  1. EPS（Encapsulated PostScript）：
  1. AI（Adobe Illustrator）：
  1. PDF（Portable Document Format）：

总结

矢量图形是一种基于几何形状和数学公式描述的图形格式，具有分辨率无关性、文件大小小、可编辑性高等优点。它们广泛应用于图形设计、网页设计、动画制作和科学绘图等领域，特别适合需要高质量、可缩放的图像场景。

光栅化在本文中的应用

在论文《An Approximate Image-Space Approach for Interactive Refraction》中，光栅化是实现交互式折射效果的关键技术之一。光栅化用于将几何图形（如折射物体的表面）转换为图像空间中的像素数据，从而为后续的图像空间计算提供基础。以下是光栅化在论文中的具体体现：

1. 光栅化在折射计算中的作用

论文提出了一种基于图像空间的折射近似方法，核心思想是利用光栅化后的信息（如入射方向、击中点、表面法线等）来近似计算折射路径。光栅化将几何体的表面转换为屏幕空间中的像素数据，使得这些信息可以直接用于后续的着色器计算。

具体体现：

2. 光栅化用于近似第二个折射点

论文中提出了一种基于光栅化的近似方法来计算第二个折射点（\(P_2\)）。具体步骤如下：

（1）计算前后表面的距离

（2）近似第二个折射点

\[\tilde{P}_2 = P_1 + \tilde{d} \vec{T}_1\]

3. 光栅化用于法线查找

为了计算第二次折射方向（\(\vec{T}_2\)），需要找到 \(\tilde{P}_2\) 处的法线（\(\vec{N}_2\)）。论文中利用光栅化将后表面的法线存储到纹理中，并在第二次遍历中通过纹理查找获取法线。

具体步骤：

4. 光栅化的效率优势

光栅化是一种高效的图形处理技术，特别适合在GPU上实现。论文中提到，该方法能够在现代图形硬件上高效运行，即使对于复杂模型也能实现高帧率的交互式渲染。光栅化提供了以下效率优势：

总结

在论文中，光栅化是实现交互式折射效果的核心技术。它不仅提供了入射方向、表面法线和深度信息，还通过纹理映射和插值方法近似计算了第二个折射点和法线。光栅化的高效性和硬件支持使得该方法能够在GPU上快速运行，适用于复杂场景的实时渲染。

原文翻译

An Approximate Image-Space Approach for Interactive Refraction

作者：Chris Wyman

单位：University of Iowa

摘要

许多交互式应用都追求逼真的渲染效果，但帧率限制通常使得真实感仅限于能够在图形硬件上高效运行的效果。折射效果在这些应用中常常被忽略。我们提出了一种简单的图像空间方法来实现折射，该方法能够在现代图形卡上轻松运行。我们的方法需要在GPU上进行两次遍历，并允许通过两个界面折射远处的环境，而现有的交互式技术仅限于单个界面。与所有基于图像的算法一样，在某些情况下可能会出现锯齿现象，但我们的方法生成的合理折射效果应该能够满足许多应用的需求。

CR Categories: I.3.7 [计算机图形学]: 三维图形与逼真度

关键词: 交互式渲染、折射、硬件

approximate-refraction.fig.1

图1：以往的交互式技术（a）仅通过单个表面发生折射[Oliveira 2000]。我们的方法（b）可以通过两个表面发生折射，帧率达到每秒53帧，并且与光线追踪（c）的结果相当。

1 引言

在许多应用中，交互性必须优先于真实感。这促使许多研究人员致力于开发近似的真实感效果，以优化速度。通过并行计算增加可用的计算能力[Wald et al. 2002]，可以使用标准的光线追踪和路径追踪技术实现交互式的真实感渲染，但高昂的成本常常限制了这种并行计算在主流应用中的使用。因此，研究人员开发了针对阴影[Assarsson and Akenine-Möller 2003; Chan and Durand 2003; Kautz et al. 2004; Wyman and Hansen 2003]、焦散[Wand and Straßer 2003; Purcell et al. 2003]、全局光照[Ng et al. 2004; Sloan et al. 2002]、反射[Ofek and Rappoport 1999]以及基本折射[Guy and Soler 2004; Schmidt 2003; Ts’o and Barsky 1987]的硬件加速近似方法。

本文针对大多数基于GPU的交互式折射算法的一个主要限制：仅允许通过单个表面的折射。在真实场景中，很少有折射仅发生在单个表面上。人们常常透过介质物体（例如一副眼镜）观察，因此处理多个界面显得尤为重要。研究人员已经提出了多种近似单表面折射的方法。一种方法利用GPU的可编程特性，计算通过可见前向多边形的折射或伪折射方向。折射颜色的确定方式包括：通过索引远处的环境贴图[Lindholm et al. 2001]或描述附近几何体的扰动纹理[Oliveira 2000]。Schmidt [2003]采用了一种几何技术，类似于Ofek和Rappoport [1999]的反射方法。Ofek的方法在反射凹形物体时存在问题，而Schmidt的方法即使在折射通过凸形物体时也会出现类似问题。在这种情况下，准确连接折射虚拟顶点以进行渲染变得非常困难。

少数研究人员考虑了多表面折射的问题。Guy和Soler [2004]交互式地渲染了简单的凸形宝石。由于他们通过解析方法计算折射顶点，并在每一帧更新结果的面片树，因此这种方法可能难以扩展到更复杂的物体。Kay和Greenburg [1979]引入了一个“厚度”参数，用于处理双面折射物体；这种方法适用于厚度均匀的物体（例如窗玻璃），但许多物体的厚度变化较大。Diefenbach和Badler [1997]采用多遍方法在图形硬件上交互式地渲染平面折射。Ohbuchi [2003]提出了一种顶点追踪预处理方法，用于在原型多媒体处理器上近似交互式折射。Heidrich等人[Heidrich et al. 1999]采用光场表示，以更高的内存消耗换取交互性。虽然本文的重点并非如此，但Hakura等人[Hakura et al. 2001]通过利用GPU资源加速了光线追踪。遗憾的是，即使同时使用CPU和GPU进行渲染，这种方法也无法实现实时结果。

2 基础折射

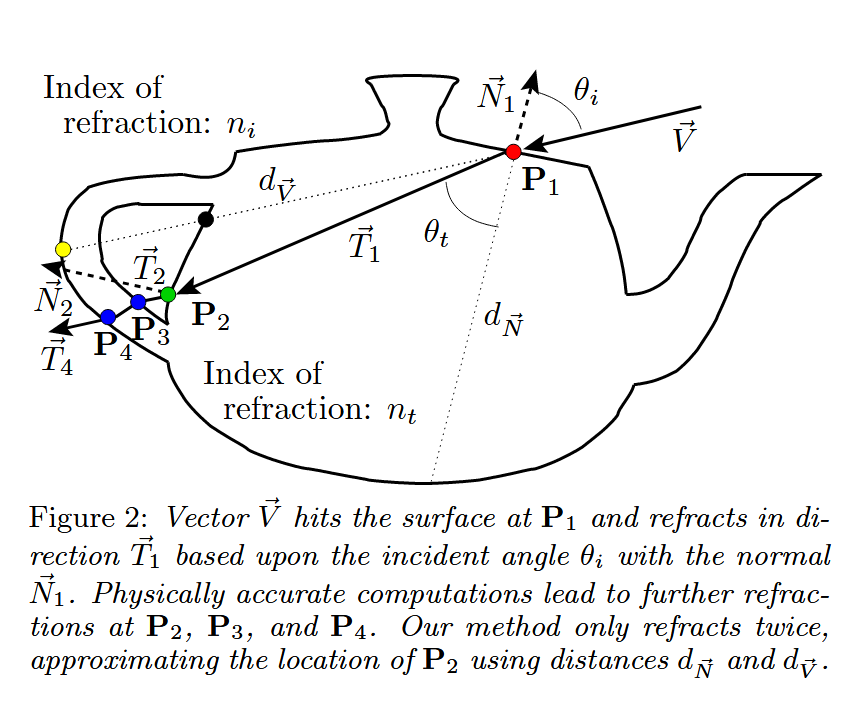
approximate-refraction.fig.2.png

图2：向量 \(\vec{V}\) 在点 \(P_1\) 处击中表面，并根据入射角 \(\theta_i\) 和法线 \(\vec{N}_1\) 的方向折射为 \(\vec{T}_1\)。物理上精确的计算会导致在 \(P_2\)、\(P_3\) 和 \(P_4\) 处进一步折射。我们的方法仅进行两次折射，使用距离 \(\tilde{d}_{\vec{N}}\) 和 \(\tilde{d}_{\vec{V}}\) 来近似 \(P_2\) 的位置。

计算通过单个界面的折射相对简单，只需已知击中点 \(P_1\) 处的表面基本信息（见图2）。折射光线的行为遵循斯涅尔定律（Snell’s Law），其表达式为：

\[n_i \sin \theta_i = n_t \sin \theta_t,\]

其中，\(n_i\) 和 \(n_t\) 分别是入射介质和透射介质的折射率。\(\theta_i\) 表示入射向量 \(\vec{V}\) 与表面法线 \(\vec{N}_1\) 之间的夹角，而 \(\theta_t\) 表示折射向量 \(\vec{T}_1\) 与法线反向量之间的夹角。在光线追踪中，折射光线会独立地与几何体相交，并递归地应用斯涅尔定律，因此通过复杂物体的折射是简单的。然而，在GPU的流式处理范式中，为不同像素执行独立操作的成本较高。以图2中的例子为例，光栅化可以确定 \(\vec{V}\)、\(P_1\) 和 \(\vec{N}_1\)，简单的片段着色器可以计算出 \(\vec{T}_1\)。遗憾的是，如果不借助加速的基于光线的方法[Purcell et al. 2003]，在GPU上精确确定点 \(P_2\) 是不可能的。由于GPU光线追踪技术相对较慢，对于复杂多边形物体的多次反射折射无法实现交互性。

3 图像空间折射

我们提出了一种不依赖于GPU光线追踪的方法，而是通过光栅化可以轻松计算的值来近似通过两个界面的折射所需的信息。考虑光栅化后已知的信息。对于每个像素，我们可以轻松获取：

利用这些信息，可以通过斯涅尔定律（Snell’s Law）轻松计算出折射方向 \(\vec{T}_1\)，例如在 Lindholm 等人 [2001] 中提到的方法。进一步考虑计算二次折射光线 \(\vec{T}_2\) 所需的信息，仅需要 \(\vec{T}_1\)、点 \(P_2\) 和法线 \(\vec{N}_2\)。由于计算 \(\vec{T}_1\) 是直接的，我们主要贡献了一种简单的方法来近似 \(P_2\) 和 \(\vec{N}_2\)。再次强调，由于准确确定这些值需要逐像素进行光线追踪，因此我们使用近似点 \(\tilde{P}_2\) 和法线 \(\vec{N}_2\)。在找到 \(\vec{T}_2\) 后，我们假设可以通过索引无限环境贴图来获取折射颜色。未来的工作可能会探索如何对附近几何体进行折射的方法。

3.1 近似点 \(P_2\)

尽管光线追踪成本过高，但它为近似第二个折射位置提供了宝贵的思路。考虑光线的参数化形式 \(P_{\text{origin}} + t \vec{V}_{\text{direction}}\)。在我们的情况下，可以写为：

\[P_2 = P_1 + d \vec{T}_1,\]

其中 \(d\) 是 \(P_2\) 和 \(P_1\) 之间的距离。已知 \(P_1\) 和 \(\vec{T}_1\)，近似位置 \(\tilde{P}_2\) 仅需找到一个近似距离 \(\tilde{d}\)，使得：

\[\tilde{P}_2 = P_1 + \tilde{d} \vec{T}_1 \approx P_1 + d \vec{T}_1.\]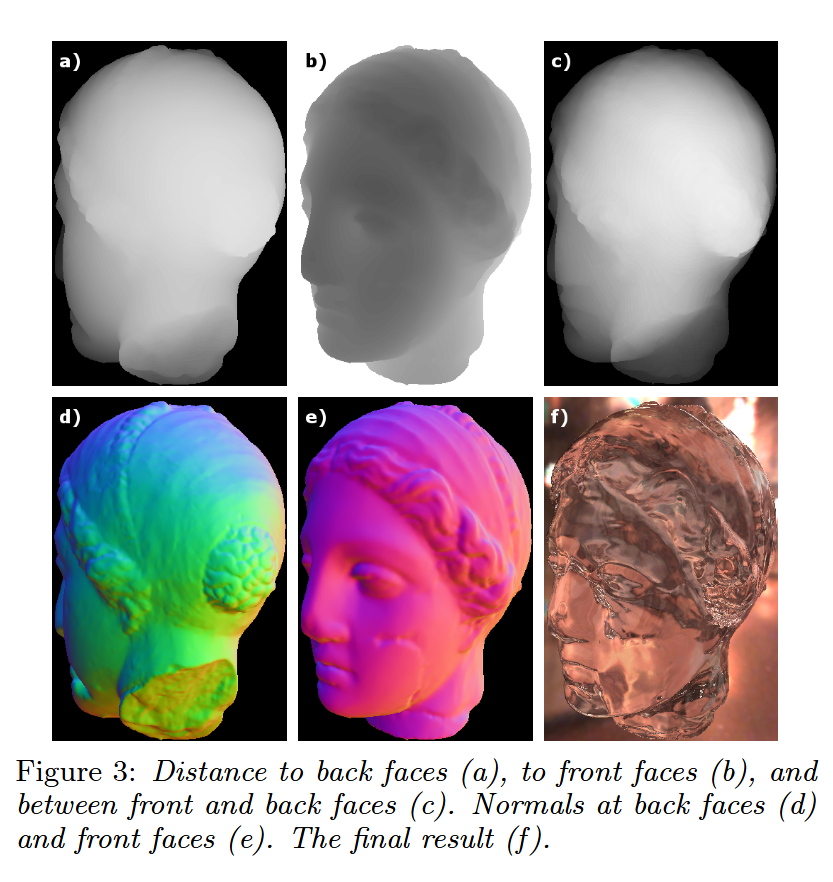

approximate-refraction.fig.3.png

图3：到后表面的距离（a）、到前表面的距离（b）以及前后表面之间的距离（c）。后表面的法线（d）和前表面的法线（e）。最终结果（f）。

最简单的近似方法是使用前后几何体之间的非折射距离 \(d_{\vec{V}}\)。通过反转深度测试（即使用 GL_GREATER 而不是 GL_LESS）渲染折射几何体，将深度缓冲区存储到纹理中（见图3a），然后正常重新渲染（见图3b），并利用两个深度缓冲区的 \(z\) 值计算距离（见图3c）。这种简单近似方法最适合于表面曲率较低且折射率较小的凸几何体。由于折射光线会向内弯曲（对于 \(n_t > n_i\)，靠近法线反方向），当 \(n_t\) 变得非常大时，\(\vec{T}_1\) 接近于 \(-\vec{N}_1\)。这表明可以基于 \(\theta_i\) 和 \(\theta_t\) 在距离 \(d_{\vec{V}}\) 和 \(d_{\vec{N}}\) 之间进行插值，以获得更准确的近似值 \(\tilde{d}\)。我们在实验中采用了这种方法，预先计算每个顶点的 \(d_{\vec{N}}\)，并通过以下公式进行插值：

\[\tilde{d} = \frac{\theta_t}{\theta_i} d_{\vec{V}} + \left(1 - \frac{\theta_t}{\theta_i}\right) d_{\vec{N}}.\]

如果以紧凑且易于访问的方式存储预先计算的 \(d\) 的采样值，可能会获得更高的精度。我们尝试将模型存储为一个 \(64^2\) 的几何图像 [Praun and Hoppe 2003]，并对几何图像中的每个纹理元素在 \(64^2\) 个方向上采样 \(d\)，得到一个 \(4096^2\) 的纹理，包含采样的 \(d\) 值。然而，对这种表示进行插值会导致明显的离散化 \(d\) 值，结果比上述方法更差。

3.2 确定法线 \(\vec{N}_2\)

approximate-refraction.fig.4.png

图4：佛像底座使用（a）最远表面或（b）第二个表面作为我们的二次折射，（c）单个折射界面，以及（d）光线追踪（光线深度为6）。

在近似得到 \(\tilde{P}_2\) 后，计算 \(\vec{T}_2\) 的最后一个需求是法线 \(\vec{N}_2\)。这些信息在每个顶点处与网格一起存储，但确定 \(\vec{T}_1\) 与哪个多边形相交的成本很高，除非我们依赖图像空间方法。考虑凸形物体的情况，我们可以使用两次遍历光栅化所有几何体：一次剔除前表面，一次剔除后表面。如果我们将第一次遍历渲染到纹理中，使用表面法线作为颜色（如图3d所示），那么在第二次遍历中，我们可以将近似的出射点 \(\tilde{P}_2\) 投影到纹理空间，并通过纹理查找来获取法线。将这种方法扩展到凸形物体之外会遇到问题，因为多个表面可能会投影到同一个 \(z\) 缓冲区纹理单元上。我们的方法可以通过更多纹理扩展到额外的折射，但如何近似进一步的交点位置（例如图2中的 \(P_3\)、\(P_4\)）尚不清楚。此外，对于许多复杂物体，两个折射界面已经能够给出合理的结果。在不扩展到更多界面的情况下，处理凹形物体有两种方法：基于到眼睛最远表面或第二个表面（即第一个背向表面）的距离来计算二次折射点 \(\tilde{P}_2\)（图2中的黄色或黑色点）。唯一的区别在于第一次遍历中渲染到纹理的表面以及后续用于计算 \(d_{\vec{V}}\) 和 \(\vec{N}_2\) 的表面。图4和图5展示了这种差异。当渲染深度复杂度较高的物体时，使用最远的多边形可以显示出用户可能期望看到的几何形状，而使用第二个多边形则可以忽略更远的多边形，从而给出更平滑的结果。对于近乎凸形的物体，这种差异几乎难以察觉。

approximate-refraction.fig.5.png

图5：马的两个视图。参考图像采用每像素64个样本的光线追踪，右侧插图比较了我们的方法在后表面或第二个表面进行二次折射的结果，以及每像素一个样本的光线追踪结果。

3.3 问题案例

这种方法存在三个问题：没有内置的方法来处理全内反射，\(\tilde{P}_2\) 可能不会投影到背向多边形上，或者由于凹性，\(\tilde{P}_2\) 可能会投影到错误的多边形上。片段着色器可以通过循环在前后表面之间反弹来处理全内反射（TIR），但这会显著减慢代码运行速度，并且会放大图像空间方法固有的误差。我们的实现禁止入射角 \(\theta_i\) 大于临界角 \(\theta_{\text{crit}}\)，并将 \(\theta_i\) 限制在 \(\theta_{\text{crit}}\)。实际上，这样的光线会“折射”到出射表面的切线方向。全内反射区域在仅有一个样本的情况下通常会很嘈杂；对于复杂物体（例如图1中的佛像），光线追踪器需要在这些区域每像素采样16次或64次才能获得无噪的结果。尽管我们的方法在物理上不够准确，但能够以每像素一个样本给出合理且相对平滑的结果。考虑 \(\tilde{d}\) 过大的情况。这会导致 \(\tilde{P}_2\) 落在折射物体轮廓之外，如图3d中的黑色纹理单元。从概念上讲，这意味着 \(\vec{T}_1\) 与物体的侧面相交。这种问题很少发生，通常出现在折射率大于1.5的凹形物体上。为了避免结果中的伪影，我们将出射法线设置为垂直于相机视向向量 \(\vec{Lat}\)。具体来说，我们将 \(\vec{T}_1\) 投影到垂直于 \(\vec{Lat}\) 的平面上（即，\(\vec{N}_2 \equiv \vec{T}_1 - (\vec{Lat} \cdot \vec{T}_1) \vec{Lat}\)）。改进 \(\tilde{d}\) 可以减少这个问题。最后一个问题是对于凹形折射体，在物体深度复杂度超过两层的区域附近。如图5所示，从最初击中马身体的视光线的近似点 \(\tilde{P}_2\) 可能会投影到腿上，尽管 \(P_2\) 实际上位于身体的远侧。尽管可以选择用于二次折射的表面，但这种问题是我们的方法的一个伪影，主要在高度凹形物体上变得令人反感。补充DVD中包含一个额外的图像，用于在每个像素基础上检查这些误差。

4 结果

我们在配备128MB内存的AGP 8x NVIDIA GeForce 6800显卡上，使用OpenGL实现了这种方法，并运用了Cg顶点着色器和片段着色器（相关内容可在DVD附带资料中获取）。该算法需要两个渲染过程。第一个过程渲染到背面多边形的距离，并存储它们的法向量，如图3a和图3d所示。第二个过程渲染正面多边形，并使用片段着色器计算折射。

假设BackfaceZBuf和BackfaceNormals是在第一个过程中计算得到的纹理，下面是该片段着色器的伪代码：

for all fragments \(F\) (given \(\mathbf{P}_1\), \(\vec{V}\), and \(\vec{N}_1\)), do

    \(\vec{T}_1 = Refract(\vec{V}, \vec{N}_1)\)

    \(d_{\vec{V}} = DistanceFrontFaceToBackFace(F, BackfaceZBuf)\)

    \(d_{\vec{N}} = DistanceAlongNormal(\mathbf{P}_1)\)

    \(\tilde{d}=WeightDistance(-\vec{N}_1 \cdot \vec{T}_1, \vec{V} \cdot \vec{T}_1, d_{\vec{V}}, d_{\vec{N}})\)

    \(\tilde{\mathbf{P}}_2 = \mathbf{P}_1 + \tilde{d}\vec{T}_1\)

    \(tex_{far} = ProjectToScreenSpace(\tilde{\mathbf{P}}_2)\)

    \(\vec{N}_2 \approx TextureLookup(tex_{far}, BackfaceNormals)\)

    \(\vec{T}_2 \approx Refract(\vec{T}_1, \vec{N}_2)\)

    return \(IndexEnvironmentMap(\vec{T}_2)\)

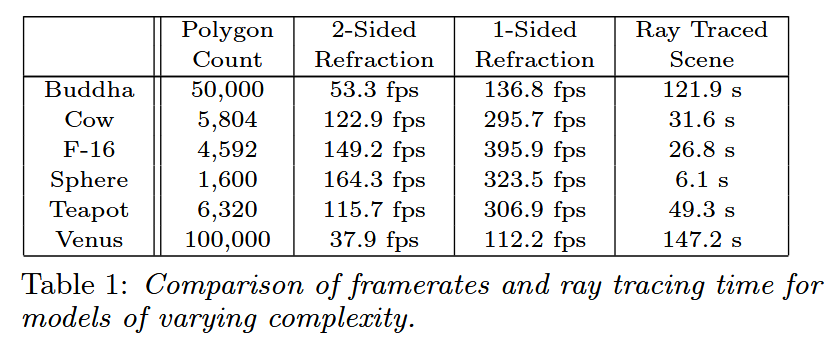
approximate-refraction.table.1.png

表1：不同复杂度模型的帧率和光线追踪时间对比。

在主频为3.0 GHz、内存为2GB的奔腾4处理器上运行，对于1024×1024分辨率的图像，我们得到的运行时间如表1所示。我们实现三种技术的代码均未经过优化，但即使对于复杂模型也能达到较高的速度。需要注意的是，部分计时数据是针对附带视频中的场景，这里未展示。

approximate-refraction.fig.6.png

图6：仅通过单个界面的折射（上）、使用我们的技术（中）以及光线追踪（下）。喷气机的折射率为1.2，球体的折射率为1.5。

我们的大多数结果使用的折射率为1.2，图6中的球体和视频中的茶壶除外，它们的折射率均为1.5。对于中等至高折射率，复杂的几何形状通常会导致折射效果显得杂乱且有噪点，即使是在经过抗锯齿处理的光线追踪图像中也是如此。在这种情况下，每个像素仅进行一次采样，无论是光线追踪还是使用我们的方法，在动画过程中都会产生明显的闪烁噪点。我们发现，OpenGL中的超采样有助于缓解这个问题，不过可能需要比我们尝试的每个像素4次采样更多的采样次数。

5 结论

本文提出了一种简单的图像空间方法，用于生成通过两个表面的合理交互式折射。该方法能够在当前的GPU上实现实时运行，即使对于相对复杂的模型也是如此。最大的限制是我们计划在未来解决的：该方法将折射限制在无限环境贴图中，不允许一个物体通过另一个物体的折射。此外，我们希望更好地处理凹形物体。未来工作的另一个方向是将交互式折射应用于快速生成焦散效果。

致谢：感谢Paul Debevec提供的光照探针，以及Jim Cremer和匿名审稿人提出的建设性意见。本研究得到了爱荷华大学Old Gold Fellowship的部分资助。

评论