链接

论文链接：ACM SIGGRAPH 1979

发表时间：Published: 01 August 1979

ACM SIGGRAPH Computer Graphics, Volume 13, Issue 2

Pages 158 - 164

论文重点难点讲解

这篇论文《TRANSPARENCY FOR COMPUTER SYNTHESIZED IMAGES》由Douglas Scott Kay和Donald Greenberg撰写，主要研究如何提高计算机合成图像中透明物体的逼真度，特别是在处理透明物体的折射和透明度方面。以下是论文的重点和难点：

论文重点

1. 透明度算法的改进

• 论文指出，传统的线性透明度算法（如公式 $ \text{FINAL} = \text{OLD} \times t + \text{NEW} \times (1 - t) $）虽然简单，但在处理透明物体时存在明显缺陷，如无法正确模拟光线通过物体时的强度变化和折射效果。

• 提出了一种非线性透明度算法，通过调整透明度与表面法线的关系，使得透明度在物体边缘逐渐减小，从而更接近真实物体的光学特性。

1. 折射效果的模拟

• 论文强调，为了使透明物体看起来更逼真，需要模拟光线通过透明物体时的折射效果。这要求算法能够正确处理光线的方向变化以及背景图像的扭曲。

• 提出了一种简化的折射算法，通过假设光线在非介质中沿Z轴平行传播，避免了复杂的光线追踪计算，同时能够合理近似折射效果。

1. 算法的实现与优化

• 论文详细描述了如何在现有的Z-buffer隐藏面算法中实现改进的透明度和折射算法。

• 提出了处理透明物体时的顺序问题（从后向前处理），并讨论了如何通过简单的几何假设（如物体表面厚度一致）来简化计算。

1. 实验结果

• 论文展示了使用改进算法生成的透明物体图像（如花瓶和香槟杯），证明了新算法在提高图像逼真度方面的有效性，同时计算成本较低。

论文难点

1. 折射效果的准确模拟

• 精确模拟折射需要对每条光线进行追踪，计算其在不同介质中的传播路径和方向变化。这在计算上非常昂贵，尤其是在复杂的场景中。

• 论文通过假设光线在非介质中平行传播来简化计算，但这种方法在某些情况下可能会引入误差，尤其是在视角较近或物体形状复杂时。

1. 透明度与折射的结合

• 透明度和折射是透明物体的两个关键特性，但同时模拟这两种效果需要在算法设计上进行权衡。论文提出的非线性透明度算法虽然在一定程度上解决了透明度问题，但在结合折射时仍需进一步优化。

1. 算法的通用性

• 论文提出的算法虽然在特定条件下效果显著，但其假设（如光线平行传播、物体表面厚度一致等）限制了其在更复杂场景中的应用。如何在更一般的情况下实现类似的逼真效果是一个挑战。

1. 计算效率与逼真度的平衡

• 论文的核心目标是在不显著增加计算成本的情况下提高图像的逼真度。然而，完全准确的折射和透明度模拟需要复杂的光线追踪技术，这与论文的目标相悖。因此，如何在计算效率和图像质量之间找到最佳平衡是一个重要的研究方向。

总结

这篇论文通过改进透明度算法和提出简化的折射算法，显著提高了计算机合成图像中透明物体的逼真度。尽管存在一些假设和局限性，但其方法在计算效率和图像质量之间取得了较好的平衡，为后续的计算机图形学研究提供了重要的参考。

论文详细讲解

这篇论文《TRANSPARENCY FOR COMPUTER SYNTHESIZED IMAGES》由Douglas Scott Kay和Donald Greenberg撰写，发表于1979年，主要研究如何提高计算机合成图像中透明物体的逼真度。论文的核心内容集中在透明度（transparency）和折射（refraction）的模拟上，提出了改进传统算法的方法，以更真实地渲染透明物体。以下是对论文的详细讲解：

1. 研究背景与动机

1.1 计算机图形学中的透明度模拟

计算机图形学的一个重要目标是生成逼真的图像，尤其是对透明物体的渲染。透明物体（如玻璃、水等）在现实世界中表现出复杂的光学特性，如光线的透射、折射和反射。然而，当时的算法在模拟这些特性时存在明显不足，导致生成的图像缺乏真实感。

1.2 传统算法的局限性

传统的透明度算法大多假设透明度是线性的，即物体的透明度在整个表面上是均匀的。这种假设虽然简单，但在处理具有曲面的透明物体时，会产生以下问题：

• 光线强度问题：光线通过物体时，其强度应与通过的材料厚度成反比，但线性算法无法模拟这种关系。

• 折射效果缺失：光线通过不同密度的介质时会发生折射，导致背景图像扭曲。传统算法通常忽略这一现象。

这些问题使得传统算法生成的透明物体图像虽然有透明感，但缺乏真实感。

2. 透明度的改进算法

2.1 线性透明度算法

线性透明度算法是最简单的透明度模拟方法。其基本思想是将背景图像与前景物体的颜色进行加权混合，公式如下：

\[\text{FINAL} = \text{OLD} \times t + \text{NEW} \times (1 - t)\]

其中：

• FINAL 是最终像素值。

• OLD 是背景图像的像素值。

• NEW 是前景物体的像素值（假设物体不透明时的颜色）。

• t 是透明度（0表示完全不透明，1表示完全透明）。

这种方法的优点是实现简单，计算成本低。然而，它无法模拟真实透明物体的光学特性，尤其是在物体边缘，光线通过的材料更多，透明度应更低。

2.2 非线性透明度算法

为了更真实地模拟透明物体，论文提出了一种非线性透明度算法。该算法的核心思想是让透明度与光线通过物体的路径长度相关。具体公式如下：

\[t = (\text{MAXT} - \text{MINT}) \times (1 - (1 - \text{NORMZ})^{\text{tpwr}}) + \text{MINT}\]

其中：

• t 是当前像素的透明度。

• MAXT 和 MINT 分别是物体上任意点的最大和最小透明度。

• NORMZ 是表面法线的Z分量（与光线方向相关）。

• tpwr 是一个指数因子，用于控制透明度的变化速度。

这种算法通过调整透明度在物体边缘逐渐减小，更接近真实物体的光学特性。例如，对于薄玻璃，可以使用较大的指数因子来模拟边缘的透明度变化。

3. 折射效果的模拟

3.1 折射的物理基础

当光线从一种介质进入另一种介质时，会发生折射。折射遵循斯涅尔定律（Snell’s Law）：

\[n_1 \sin \theta_1 = n_2 \sin \theta_2\]

其中：

• $n_1$ 和 $n_2$ 分别是两种介质的折射率。

• $\theta_1$ 和 $\theta_2$ 分别是入射角和折射角。

折射会导致光线方向的改变，进而影响背景图像的扭曲和光线强度的变化。

3.2 折射模拟的难点

精确模拟折射需要对每条光线进行追踪，计算其在不同介质中的传播路径和方向变化。这在计算上非常昂贵，尤其是在复杂的场景中。此外，传统的隐藏面算法假设光线沿直线传播，无法直接处理折射现象。

3.3 简化的折射算法

论文提出了一种简化的折射算法，通过以下假设降低计算复杂度：

1. 光线在非介质中沿Z轴平行传播：这使得光线的当前X、Y位置可以确定其下一个交点。

2. 所有表面可以直接“看到”光源：避免了对漫反射和镜面反射光线的追踪。

基于这些假设，算法的主要步骤如下：

1. 计算折射光线的方向：根据斯涅尔定律，计算光线进入和离开介质时的新方向。

2. 确定光线的传播路径：根据光线进入和离开的位置，计算其在介质中的传播距离。

3. 调整背景图像的扭曲：根据光线的传播路径，调整背景图像的X、Y位置。

4. 计算透明度：根据光线通过的材料厚度，计算透明度。

4. 算法实现与优化

4.1 实现细节

论文将改进的透明度和折射算法集成到Z-buffer隐藏面算法中。具体步骤如下：

1. 从后向前处理表面：将背景图像放入图像缓冲区，然后逐个处理前景物体。每个物体的背景图像需要从前一个物体的图像中采样。

2. 临时存储像素值：在处理每个表面时，临时存储像素值，直到整个表面处理完成后再更新图像缓冲区。这确保了后续物体能够看到已经折射的背景图像。

4.2 优化与假设

论文通过以下假设简化计算：

• 光线在非介质中平行传播：减少了光线方向变化的复杂性。

• 物体表面厚度一致：避免了复杂的几何计算。

• 忽略反射光线的追踪：假设所有表面可以直接“看到”光源，避免了对反射光线的复杂计算。

这些假设虽然引入了一些误差，但在大多数情况下，生成的图像仍然具有较高的真实感。

5. 实验结果与评估

论文展示了使用改进算法生成的透明物体图像，如花瓶和香槟杯。实验结果表明：

• 透明度变化自然：物体边缘的透明度逐渐减小，更接近真实物体。

• 折射效果明显：背景图像在通过透明物体时发生扭曲，增强了真实感。

• 计算效率高：相比传统的光线追踪方法，该算法在计算成本上显著降低。

然而，论文也指出了一些局限性：

• 假设引入的误差：在视角较近或物体形状复杂时，假设可能导致误差。

• 通用性有限：算法对物体的几何形状和场景布局有一定要求，可能不适用于所有情况。

6. 结论与展望

论文提出了一种改进的透明度和折射算法，通过简化计算和合理假设，在不显著增加计算成本的情况下，显著提高了透明物体图像的真实感。尽管存在一些局限性，但这种方法为后续的计算机图形学研究提供了重要的参考。未来的研究可以进一步优化算法，减少假设带来的误差，或者结合光线追踪技术，实现更高效且逼真的透明物体渲染。

总结

这篇论文的核心贡献在于提出了一种改进的透明度和折射算法，通过非线性透明度函数和简化的折射模型，解决了传统算法的不足，提高了透明物体图像的真实感。尽管计算复杂度有所增加，但通过合理假设，算法仍然保持了较高的计算效率。论文不仅为透明物体的渲染提供了新的思路，也为计算机图形学的发展奠定了重要基础。

论文方法部分详解

以下是论文中“方法部分”的详细翻译和讲解，重点关注第4节“一种简单的折射算法（A SIMPLE REFRACTION ALGORITHM）”：

4. 一种简单的折射算法

尽管准确模拟折射在计算上代价过高，但应该可以在更低的成本下获得合理的近似效果。这里提出的算法对环境做出了一些简化的假设，但生成的透明物体图像似乎表现出折射效果。该算法将结合到使用Z-buffer隐藏面方法的平滑着色系统中进行实现，但可以推广到任何类型的着色系统。

4.1 假设

与准确折射模拟相关的最大计算负担是确定每条视线射线在每次方向变化时与每个表面的交点。因此，这里做出两个主要的简化假设：

1. 光线在非介质中沿Z轴平行传播：这允许物体通过透视变换进行扭曲，其显著优势是射线的当前X、Y位置决定了它将下一个交点的表面。

2. 所有表面可以直接“看到”光源：尽管它们实际上可能被其他透明表面遮挡。因此，完全避免了从表面向外追踪漫反射和镜面反射光线。

4.2 算法

在做出这两个假设后，折射问题简化为对前面讨论的简单透明度算法的轻微修改。两种方法之间的区别在于：

1. 背景图像中已经存在于图像缓冲区中的OLD值不一定与NEW值位于相同的X、Y位置。

2. 透明度值$t$不是常数，而是光线实际穿过的材料量的函数。

因此，这种方法需要：

A) 一种确定折射射线方向的方法；

B) 一种确定用于OLD值的X、Y位置的程序；

C) 一些决定处理表面顺序的规则。

A) 向量折射算法

当一条视线射线在某一点击中表面时，描述表面法线方向和射线方向的单位向量都是已知的。问题是根据斯涅尔定律确定视线射线的新方向。斯涅尔定律描述了光线穿过不同密度介质边界时方向的变化，定义如下：

\[n_1 \sin \theta_1 = n_2 \sin \theta_2 \quad (3)\]

其中：

• $n_1$ = 第一种介质的折射率

• $n_2$ = 第二种介质的折射率

• $\theta_1$ = 入射光线与法向量之间的夹角

• $\theta_2$ = 折射光线与法向量之间的夹角

为了找到折射向量（R），假设入射向量（I）从空气（折射率等于1）进入一种折射率为$n$的材料，并且所有向量都是单位长度。首先计算折射向量的正弦值：

\[\mathbf{S} = \frac{1}{n} (\mathbf{I} - (\mathbf{I} \cdot \mathbf{N}) \mathbf{N}) \quad (4)\]

其中：

• S = 其大小为折射向量正弦值的向量

• I = 入射向量

• N = 法向量

然后通过以下公式找到折射向量（R）：

\[\mathbf{R} = \frac{\mathbf{S}}{\|\mathbf{S}\|} \sqrt{1 - \|\mathbf{S}\|^2} \quad (5)\]

其中 $|\mathbf{S}|$ 表示向量的大小。

B) 背景的扭曲

折射的效果是光线在进入介质时改变方向，传播一段有限距离后再次改变方向并离开。由于折射算法假设视线射线在介质外总是与Z轴平行，因此只需要确定射线从介质中出来的位置，给定其进入位置和方向。

为了追踪光线在介质中的路径，需要为每个表面定义一个厚度。该算法假设这个厚度在表面上任何点的法线方向上是恒定的，并且是沿着远离观察者的方向测量的（见图8）。这实际上创建了一个不连续的表面。厚度的单位是任意的，但一旦定义，材料的透明度必须以这些单位来指定。过程如下：

1. 找到定义射线进入介质后新方向的单位向量，如前所述。

2. 找到射线在离开另一侧之前在介质内必须传播的距离。

3. 将新单位向量的分量乘以该距离，以提供X和Y方向上的偏移量。

4. 将这些增量值加到当前X、Y位置上，得到射线离开介质时的位置。

光线的强度可以通过以下公式计算：

\[t = T \cdot d \quad (6)\]

其中：

• t = 当前射线路径的总透明度

• T = 单位距离的透明度

• d = 射线在介质中传播的距离

由于射线在介质中传播的距离已在步骤2中确定，可以将其代入公式（6）以得到当前像素的透明度值。

C) 实现注意事项

在图像缓冲区的背景下讨论这种折射算法的实现，其中背景图像首先放入缓冲区，然后每个新表面被放置在现有图像之上，根据需要进行修改。为了生成一致质量的图像，必须遵循某些特定程序：

1. 按从后向前的顺序处理表面：这是必要的，因为每个表面都将当前背景图像映射到其上。标准的Z-buffer算法以随机顺序处理表面，并且只保留描述最前面表面的信息。因此，可能需要多次遍历物体环境，每次找到下一个最靠后的表面，直到所有表面都被处理（见图9）。

2. 临时存储像素值：在处理每个表面时，必须临时存储每个像素的值，直到整个表面完成。然后，所有新值应替换背景图像中的值。这确保了剩余表面看到的图像是已经被前面的表面折射过的。

注意：通常显示的许多透明物体具有简单的几何形状，通常由凸多面体定义。在这种情况下，可能可以对物体本身进行非常简单的Z排序，然后使用法向量的Z分量先处理每个物体的后表面，再处理前表面。

4.3 评估

该算法对环境做出的假设大大减少了模拟折射所需的计算量，而不会产生过多的误差（见图10、11、12）。由于所有光线在不在介质中时都被认为与Z轴平行，因此最终模拟中的误差主要是实际透视视图的函数。如果观察者距离物体足够远，所有视线射线都将几乎平行。同样，如果背景非常接近物体，从物体中发散的视线射线将在传播任何显著距离之前立即击中背景物体。

假设光线从介质中出来的表面方向与进入时相同，并不会带来严重限制。虽然可以保留更多关于物体特征的信息，但这将大大复杂化整个过程。显然，如果介质非常厚，射线出来的表面可能与进入的表面方向不同。幸运的是，透明玻璃和塑料容器——这些类型的计算机合成图像中最常见的对象——通常具有薄表面且形状规则。对于这些情况，误差很小。

这种方法的另一个优点是强度模型更加准确，因为它严格基于光线传播的距离。尽管这个距离仍然是一个近似值，但与实际光线追踪相比，相对误差很小，即使在非最佳条件下也很少出现问题。

原文翻译

计算机合成图像的透明度

道格拉斯·斯科特·凯* 和唐纳德·格林伯格

康奈尔大学计算机图形学项目

摘要

假定在整个表面上具有线性透明度的简单透明度算法，是常用于生成具有弯曲表面的透明物体的计算机合成图像的类型。尽管大多数使用这些算法创建的图像确实给人以透明的印象，但它们通常看起来并不真实。最严重的问题之一是，透过物体传输的光的强度通常与光必须穿过的材料量不成比例。另一个问题是，在物体后面看到的图像没有像光在穿过不同密度的材料而发生折射时那样发生自然的扭曲。

使用非线性透明度算法可以以较小的额外成本显著提高图像的真实感。使透明度与表面法线成正比，会使其在光线穿过物体的路径较长的表面边缘处降低。然而，精确的折射模拟需要从观察者通过图像平面并穿过每个透明物体对每条光线进行单独追踪，直到与不透明表面相交。由于每次进入不同光学密度的材料时光线的方向都会改变，所需的隐藏表面计算将非常耗时。但是，如果对每个物体的几何形状以及观察它们的条件做出一些假设，则可以使用一个简单得多的算法来近似折射效果。该方法按从后到前的顺序进行，将当前背景图像映射到下一个表面，直到所有表面都已考虑在内。

计算评论分类：8.1，8.2

关键词：透明度，折射，着色，图像合成，计算机图形学

1 引言

计算机图形学中一个备受关注的方面是数学定义对象的着色图像生成[(3),(5),(12)]。如今，计算机合成的图像已难以与真实物体的照片区分开来。这种增强的真实感在很大程度上得益于考虑常见材料表面属性，并模拟纹理、反射和阴影等细节的新技术[(1),(2),(4),(7)]。

图像合成中仍存在一定不足的一个领域是透明材料的模拟。尽管使用现有算法创建的大多数图像确实给人以透明的印象[(10)]，但由于以下两个因素，它们通常无法呈现出令人信服的真实感：

• a) 透过物体传输的光的强度通常与光必须穿过的材料量不成比例。

• b) 在物体后面看到的图像没有像光在穿过不同密度的材料而发生折射时那样发生自然的扭曲。

大多数现有的透明度模拟算法仅处理背景图像强度的修改，而不涉及模拟折射效果。最近在光线追踪方面的研究工作开发出了能够精确模拟折射效果的系统，但计算成本过高[(9),(11)]。下一节将简要讨论简化的透明度算法。随后将讨论与折射模拟相关的问题，以及对简单算法的改进建议，该改进算法可以在不显著增加计算时间的情况下近似折射效果并改进强度函数。

2 强度

为了确定当透明物体置于前景时，背景图像的强度应如何变化，研究一个真实的透明物体是很有帮助的。透过物体的大部分区域去看，通常能够清晰地看到背景，且背景光强度几乎保持完整。只有在物体边缘附近，光线需要穿过更多的材料，折射效果最为显著，此时透过物体的光线强度才会降低。这是一个合适的透明度算法应该实现的效果。

2.1 线性算法

模拟透明度的简单算法仅包含一个线性强度函数，可总结如下[(10)]。首先创建并存储背景图像。然后将透明物体的图像“绘制”在背景图像上。每个像素的颜色根据以下公式确定：

\[\text{FINAL} = \text{OLD} * t + \text{NEW} * (1 - t) \tag{1}\]

其中：

• $\text{FINAL}$ = 最终图像的像素值

• $\text{OLD}$ = 当前存储的背景图像的像素值

• $\text{NEW}$ = 假设物体为不透明时计算出的着色值。该值是表面法线与光源之间角度的函数

• $t$ = 物体的透明度（0到1之间）

• 当 $t = 0$ 时，物体完全不透明

• 当 $t = 1$ 时，物体完全透明

这种方法有效地对背景图像和正在着色的物体进行加权，以产生合适的组合。

线性近似算法确实有一些优点。由于其简单性，对平滑着色算法进行实现修改较为容易。处理时间的增加几乎完全取决于读取存储的背景图像所需的工作量。

在非常简单的环境中，例如光源位于观察者处，这种模拟可能就足够了（图1）。不幸的是，这种简单的算法不能准确地表示真实材料的光学特性。因此，会很快出现许多问题，特别是当透明度因子较高，或者光源位于观察者位置以外的其他位置时。

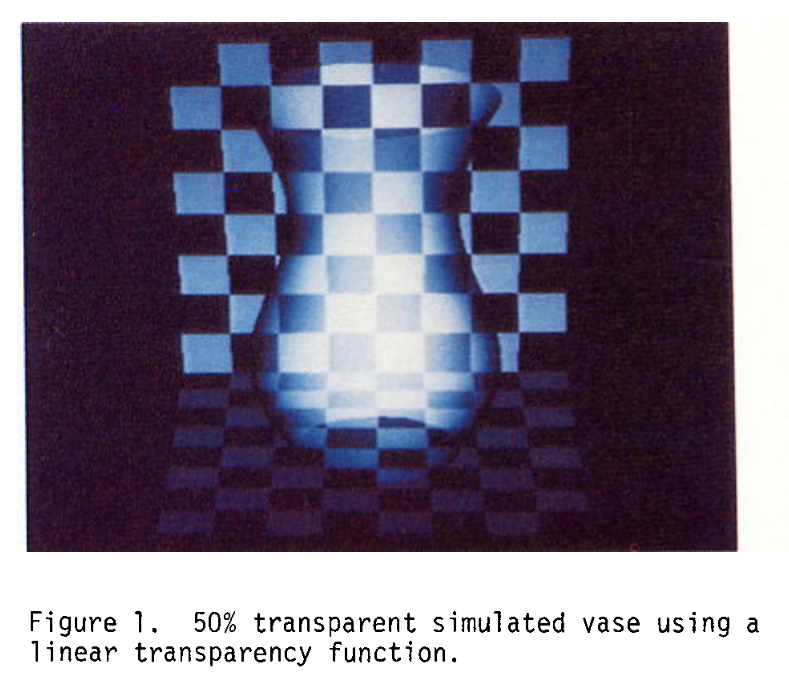
图1：使用线性透明度函数模拟的50%透明的花瓶。

2.2 非线性算法

简单透明度算法存在的问题，主要是由控制透明度程度的线性函数导致的，对于弯曲表面而言，该函数非常不准确。理想情况下，透明度应与光线必须穿过的材料量相关。对于弯曲表面的首次近似，应确保在边缘附近透明度降低[(6)]。这可以通过如下函数实现：

\[\begin{align*} t =& (\text{MAXT} - \text{MINT}) * (1 - (1 - \text{NORMZ})^{\text{tpwr}}) \\ &+ \text{MINT} \tag{2} \end{align*}\]

其中：

• $t$ = 如公式(1) 中所示的当前像素的透明度

• $\text{MAXT}$ = 物体上任意点的最大透明度

• $\text{MINT}$ = 物体上任意点的最小透明度

• $\text{NORMZ}$ = 表面单位法向量的 $Z$ 分量

• $\text{tpwr}$ = 余弦幂因子

请注意，通过使用已知的法向量Z分量（计算着色值时也需要该分量），可将额外的计算量减到最小。如有必要，应调整 $\text{NORMZ}$ 使其始终为正。当指数值为典型的2或3时，该函数在物体的大部分区域产生相对稳定的透明度，并在边缘附近迅速降为0。

图2：透明度幂因子为1的模拟透明花瓶。

无论环境配置如何，透明度最终由表面的方向控制（图2）。可以使用不同的指数来模拟各种类型材料的透明度。对于非常薄的玻璃，通过使用较大的指数，可以在边缘处得到一条透明度较低的细线。

请注意，镜面反射可增强真实感，并且在该算法中，在确定透明度后，镜面反射值总会被加到最终值中。它们不会直接影响透明度函数。

3 折射

通过对折射效果进行建模，可以提高这些模拟图像的真实感。需要一种算法，它能根据折射定律对背景图像进行扭曲，并将其映射到物体表面，同时又不会大幅增加计算时间。这种算法还应根据光线传播所经过的材料量，来确定每个像素的正确强度。

为了确定计算机生成的着色图像中任意像素的颜色，至少在概念上，有必要从观察者处发射一条视线，使其穿过图像平面上的该像素位置，并确定它与场景中的物体在哪里相交。如果场景中的所有物体都是不透明的，那么相交的最近物体将决定该像素的颜色，其他所有表面对观察者来说都是不可见的。如果有些表面是透明的，那么就需要考虑视线路径上各种物体的累积效果。对于折射模拟，难点在于所有隐藏面算法都假定视线总是沿直线传播。

a) 透视空间

大多数隐藏面算法采用的标准过程是对每个物体进行透视变换，使得由单条视线看到的所有点都具有相同的X和Y坐标。因此，要确定每个像素的颜色，只需比较每个像素位置处所有表面的Z值即可。通常，法向量保持不变换，这样它们就能得出与光源相关的正确着色值。

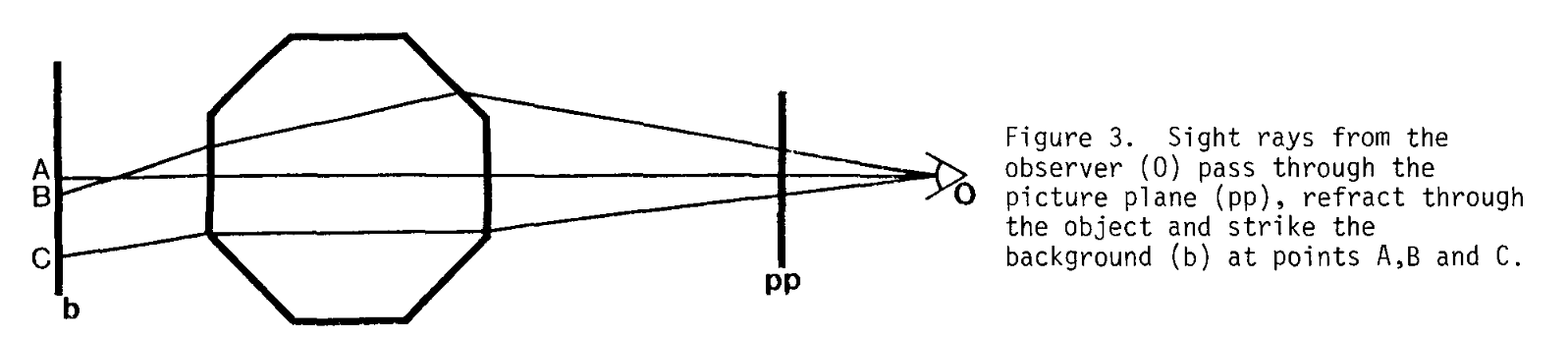
图3：来自观察者（O）的视线穿过图像平面（pp），经物体折射后，在A、B、C点处到达背景（b）。

图4：对物体应用透视变形，导致视线在错误的位置B’和C’处到达背景。

图5：补偿透视变形以产生正确的折射角度，但仍会使光线在错误的位置B’‘和C’‘处到达背景。

在模拟折射时，每当视线碰到新的透明表面，其方向都必须修改。视线与表面法线之间的角度控制着这个方向（图3）。然而，大多数透视变换首先在透视空间中使物体变形，然后使用正交投影创建图像。这样一来，视线与变形表面所成的角度会出错，新的光线方向也会出错（图4）。即使保留了足够的信息来正确确定新方向，表面之间的距离仍然会不正确。这可能会导致基于光线穿过材料量的强度函数出错，并且新方向的视线可能会射到错误的位置（图5）。

通过使用成本更高的物体空间算法进行隐藏面计算，或者在图像空间和物体空间之间进行变换以保持正确的方向，大多数这些错误是可以避免的。

b) 光线追踪

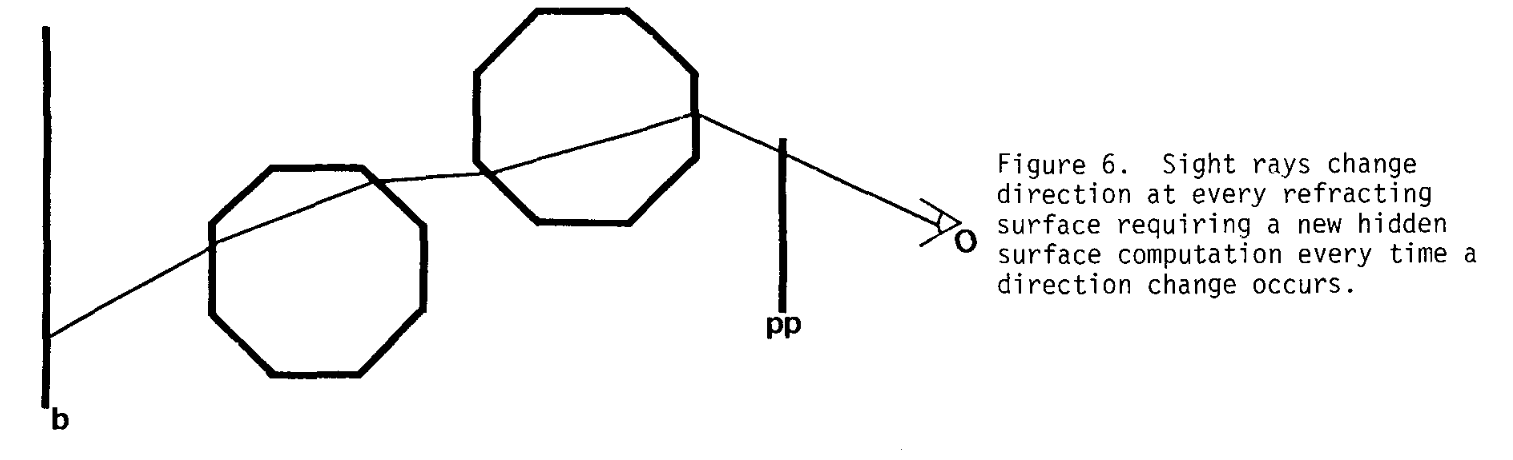
图6：视线在每个折射表面处改变方向，每次方向改变时都需要进行新的隐藏面计算。

当视线碰到透明表面时，其方向会发生改变。为了模拟折射，在给定新方向的情况下，有必要确定视线能看到什么。这本质上要求每次视线方向改变时，都要进行一次新的隐藏面计算。这个过程必须持续，直到光线到达不透明表面或背景（图6）。

第一次进行的隐藏面计算相对容易，因为所有视线都有相同的原点，且它们的方向都相互关联。然而，除非场景中的所有透明物体都具有相同的简单几何形状，否则一旦光线发生折射，没有一种变换能够预测任何视线的方向或位置。因此，为了进行精确模拟，每次视线方向改变时，都必须为每条视线执行复杂的隐藏面计算过程。

c) 漫反射和镜面反射

表面的可见性是由于光线透过该表面传播。并非完全透明的表面通常会漫反射一部分光线。用于这种反射类型的模型通常假定光源可以被物体表面直接“看到”。

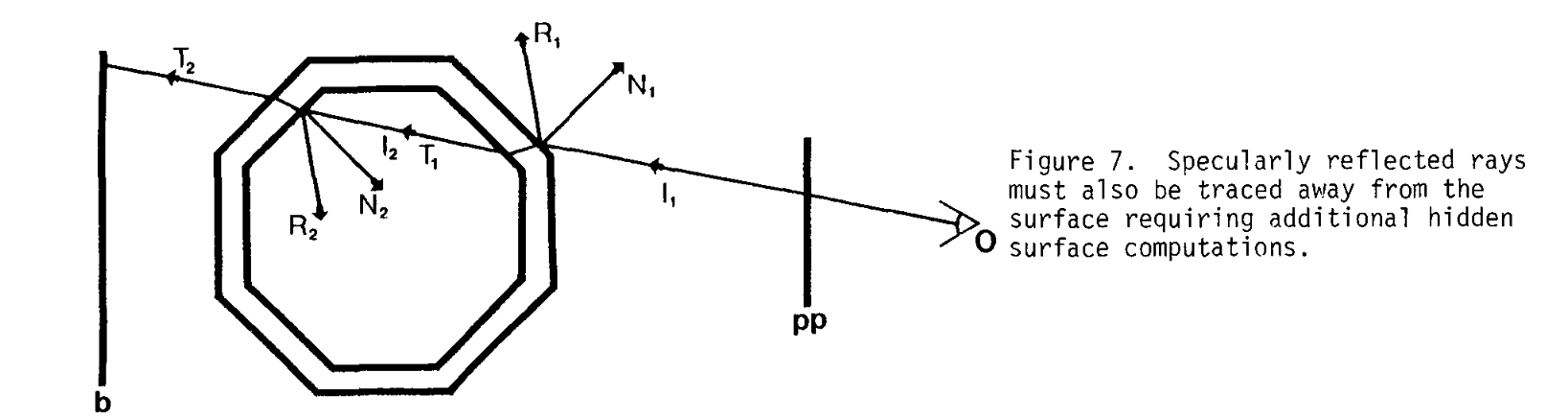
图7：镜面反射光线也必须从表面向外追踪，这需要额外的隐藏面计算。

对于生成逼真图像而言，可能更关键的是对镜面反射的考虑。为了正确确定表面上某一特定点的镜面反射值，必须考虑视线的方向和光源的位置。除非将视线追踪到表面，然后再沿反射方向返回，否则无法确定反射光线是否能“看到”光源。当然，任意点与光源之间的中间表面的折射特性会影响镜面反射（图7）。从本质上讲，对于每一条镜面反射光线，都必须像对透射光线一样进行隐藏面计算。

4 一种简单的折射算法

尽管精确的折射模拟计算量极大，但应该有可能以低得多的成本获得合理的近似值。这里提出的算法对环境做了一些简化假设，但能生成看起来有折射效果的透明物体图像。该算法将结合其在使用Z缓冲隐藏面方法的平滑着色系统中的实现进行描述。不过，它可以推广到任何类型的着色系统。

4.1 假设

精确折射模拟相关的最大计算负担在于，确定每条视线在每次方向改变时与每个表面的交点位置。因此，将做出两个主要的简化假设。第一个假设是，视线在非介质中时沿Z轴平行传播。这使得物体可以通过透视变换进行扭曲，其显著优势在于光线当前的X、Y位置能确定它接下来将与哪个表面相交。第二个假设是，所有表面都能直接“看到”光源，尽管实际上它们可能会被其他透明表面遮挡。这样，就完全避免了对从表面发出的漫反射光线和镜面反射光线的追踪。

4.2 算法

一旦做出这两个假设，折射问题就简化为对之前讨论的简单透明度算法的微小修改。这两种方法的区别在于：

1）图像缓冲区中已有的背景图像的“OLD”值，不一定与“NEW”值处于相同的X、Y位置。

2）透明度值t不是一个常数，而是光线实际穿过材料量的函数。

因此，这种方法需要：

A）确定折射光线方向的方法；

B）找到用于“OLD”值的X、Y位置的过程；

C）一些用于确定处理表面顺序的规则。

A）向量折射算法

当视线在某一特定点与表面相交时，描述表面法向方向的单位向量和光线本身的向量方向都是已知的。问题在于根据斯涅尔定律确定视线的新方向。该定律描述了光线穿过两种不同密度材料的边界时方向的变化，其定义如下：

\[n_1 \sin \theta_1 = n_2 \sin \theta_2 \tag{3}\]

其中：

• $n_1$ = 第一种介质的折射率

• $n_2$ = 第二种介质的折射率

• $\theta_1$ = 入射光线与法向量之间的夹角

• $\theta_2$ = 折射光线与法向量之间的夹角

使用折射算法时，确定折射光线的新方向存在困难，因为每个向量在概念上都可以在三维空间中任意定位。从概念上讲，为了找到折射光线的新方向，需旋转这两个向量，使其位于同一平面内，根据斯涅尔定律修改两个向量之间的夹角，然后再旋转回它们原来的方向。以下方法可以轻松确定折射光线的方向，并且避免了对相关角度的具体计算。

假设入射向量（$I$）从空气（折射率等于1）射入折射率为$n$的材料中，且所有向量均为单位长度。为了找到折射向量（$R$），首先通过以下公式计算折射向量的正弦值：

\[S = \frac{1}{n} (I - (I \cdot N) N) \tag{4}\]

其中：

• $S$ = 大小为折射向量正弦值的向量

• $I$ = 入射向量

• $N$ = 法向量

然后通过以下公式找到折射向量（$R$）：

\[R = S + \sqrt{1 - \lvert S \rvert ^2} N \tag{5}\]

其中：

• $\lvert \rvert$ = 表示向量的大小

B）背景扭曲

折射的效果是光线在进入介质时改变方向，传播一段有限的距离，然后在射出时再次改变方向。由于折射算法假定视线除了在介质内部外总是平行于Z轴，所以只需根据光线的入射位置和方向，确定光线从介质中射出的位置。

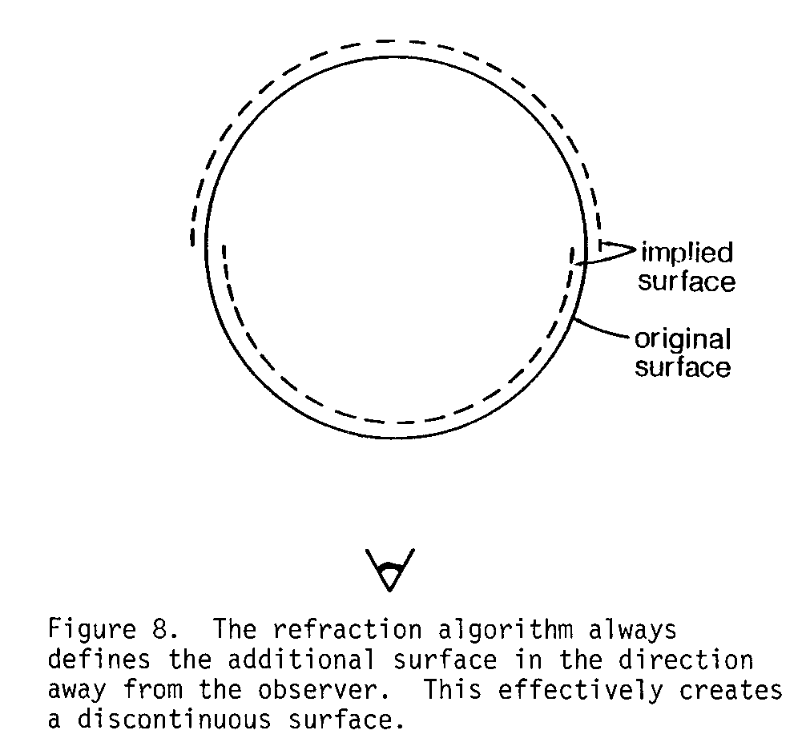
图8：折射算法总是在远离观察者的方向上定义额外的表面。这实际上创建了一个不连续的表面。

为了能够追踪光线在介质中传播的路径，需要每个表面都有一个确定的厚度。该算法假定从表面上的任何一点沿法向方向的厚度是恒定的，并且是从远离观察者的方向进行测量的（图8）。这实际上创建了一个不连续的表面。厚度的单位是任意的，但一旦确定，材料的透明度就必须用这些单位来指定。过程如下：

1）找到一个单位向量，用于确定光线进入介质后的新方向，方法如前所述。

2）计算光线在从介质另一侧射出之前，在介质中必须传播的距离。

3）将新单位向量的各个分量乘以该距离，得到在X和Y方向上的偏移量。

4）将这些增量值加到当前的X、Y位置上，得到光线从介质中射出时的位置。

透射光线的强度可由以下公式得出：

\[t = T^d \tag{6}\]

其中：

• $t$ = 当前光线总路径的透明度

• $T$ = 单位距离的透明度

• $d$ = 光线穿过介质的路径距离单位

由于光线在材料中必须传播的距离已在上述步骤（2）中确定，可将其代入公式（6），从而得到当前像素的透明度值。

C）实现注意事项

这种折射算法的实现是在图像缓冲区的背景下讨论的，即先将背景图像放入缓冲区，然后将每个新表面放置在现有图像之上，并根据需要对其进行修改。为了生成质量一致的图像，必须遵循某些特定步骤。

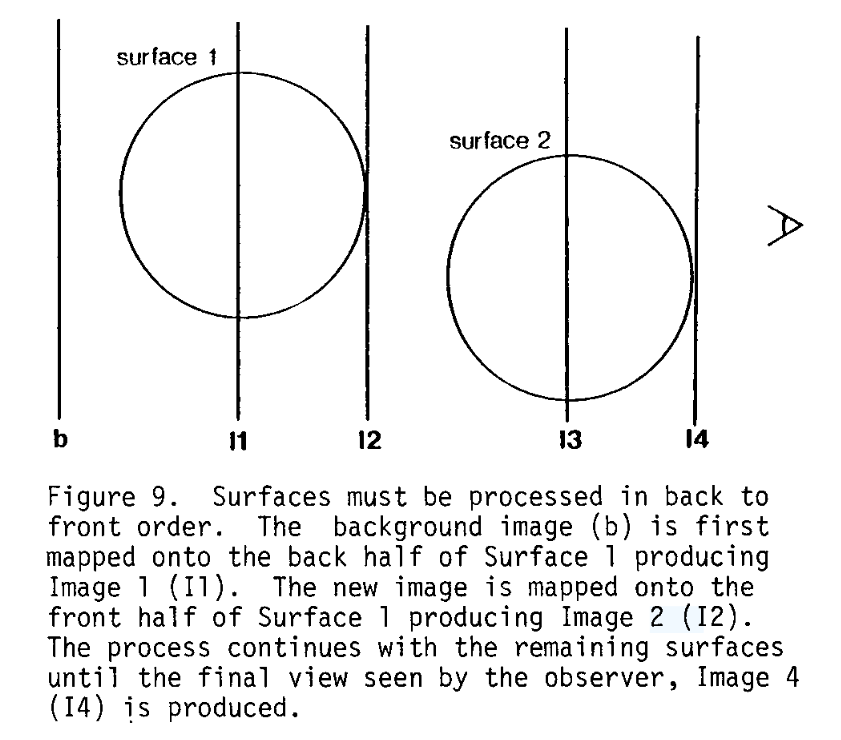
图9：表面必须按从后到前的顺序处理。首先将背景图像（b）映射到表面1的后半部分，生成图像1（I1）。然后将新图像映射到表面1的前半部分，生成图像2（I2）。该过程对其余表面继续进行，直到生成观察者看到的最终视图，即图像4（I4）。

1）表面必须按从后到前的顺序处理。这是必要的，因为每个表面都有当前的背景图像映射到其上。不幸的是，标准的Z缓冲算法以随机顺序处理表面，并且仅保留描绘最前面表面的信息。因此，可能需要对场景中的物体进行多次遍历，每次遍历找到下一个最后面的表面，直到每个表面都被处理完毕（图9）。

2）在处理每个表面时，每个像素的值必须暂时存储，直到整个表面处理完成。然后，所有新值应替换背景图像中的值。这确保了后续表面将看到已经被前面的表面折射过的图像。

值得注意的是，许多通常显示的透明物体具有简单的凸几何形状，通常由凸多面体定义。在这种情况下，可能可以对物体本身进行非常简单的Z排序，然后使用法向量的Z分量，在处理每个物体的前表面之前，先处理每个后表面。

4.3 评估

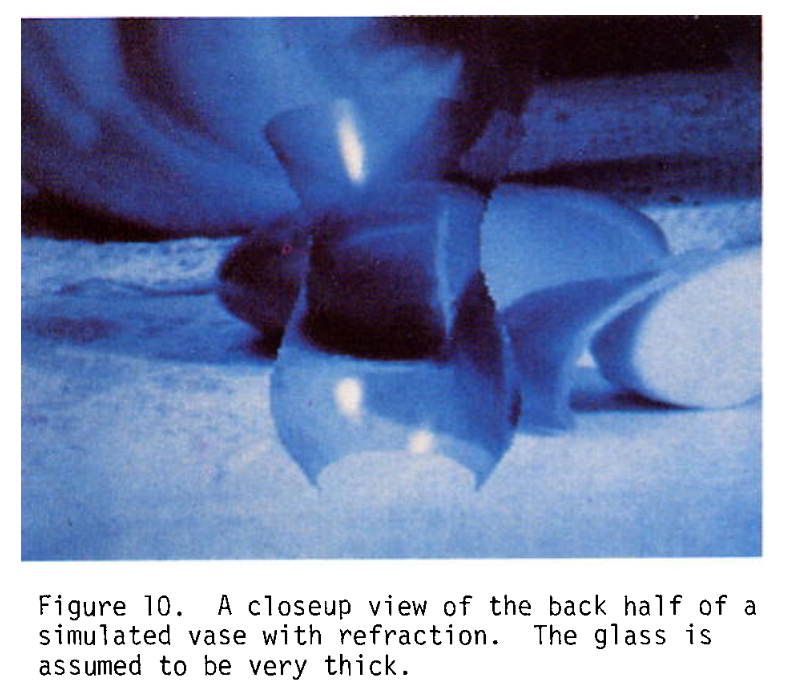
图10：模拟的带折射效果的花瓶后半部分特写，假定玻璃很厚。

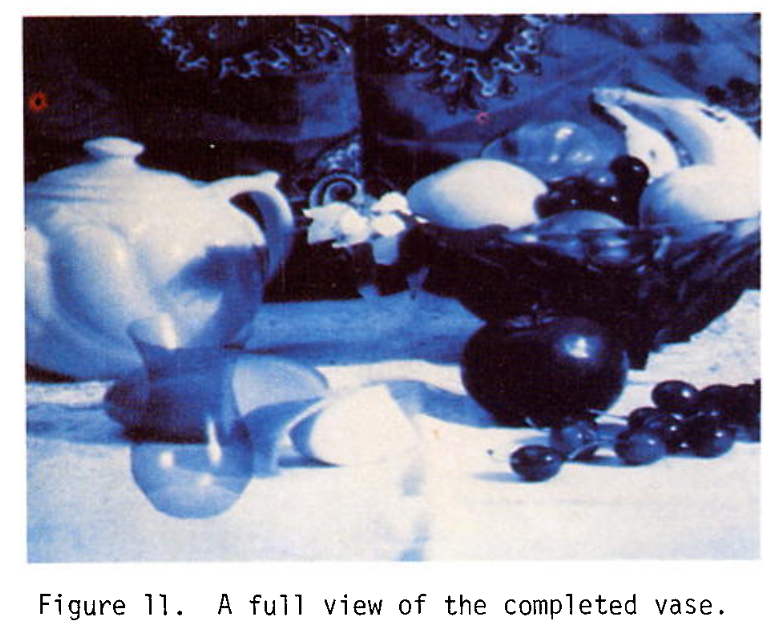
图11：完整花瓶的全貌。

图12：模拟的带折射效果的香槟杯，假定玻璃很薄。

该算法对环境所做的假设极大地减少了模拟折射所需的工作量，同时又不会产生过多误差（图10、11、12）。由于所有光线在非介质内部时都被视为平行于Z轴，最终模拟中的误差在很大程度上取决于实际透视视图的偏差程度。如果观察者离物体很远，所有视线几乎平行。同样，如果背景离物体很近，从物体射出的发散视线在传播一段显著距离之前就会立即碰到背景物体。

关于视线从介质射出的表面方向与进入时相同的假设，并不会带来严重限制。可以保留更多关于物体特性的信息，但这会使过程大大复杂化。显然，如果介质很厚，射出表面的方向可能与进入表面的方向不同。幸运的是，作为这类计算机合成图像最常见主体的透明玻璃和塑料容器，表面很薄且通常形状规则。对于这些情况，误差是微小的。

这种方法的另一个优点是强度模型更加准确，因为它严格基于光线传播的距离。尽管这个距离仍然是一个近似值，但与实际光线追踪相比，相对偏差很小，因此即使在非最优条件下也很少会成为问题。

5 结论

本文提出了一种新方法，用于提高计算机合成的透明物体图像的真实感。该算法考虑了每条视线在透过透明表面时的方向变化，并根据光线必须穿过的材料量来生成表观强度。重点在于在不过度增加计算时间的情况下生成逼真的图像。尽管现有的光线追踪系统在大多数情况下能产生准确的结果，但其计算成本通常使其不切实际。结合这两种方法，可能是在合理时间内逼真模拟复杂环境图像问题的解决方案。

致谢

作者衷心感谢使用S.C. Wu开发的放样曲面描述方法，该方法用于描述计算机合成图像。本工作是在康奈尔大学计算机图形学项目中进行的，部分由美国国家科学基金会资助 。