论文重点难点讲解

论文重点

研究背景与目标：论文提出了一种基于高斯绘制（Gaussian Splatting）的稀疏视图表面重建方法FatesGS，旨在解决现有方法在稀疏输入视图下重建质量差、训练速度慢的问题。传统方法在稀疏视图下容易过拟合，导致重建表面不完整且噪声较多。

核心贡献：

• 提出了一种结合单视图深度一致性和多视图特征一致性的稀疏视图重建框架，有效提升了重建精度和速度。

• 通过将3D高斯椭球体简化为2D椭圆高斯，并利用2D高斯绘制优化高斯原语属性，实现了更精确的几何表示。

• 在DTU和BlendedMVS数据集上验证了该方法的优越性，相比现有方法在速度上提升60倍至200倍，同时重建精度更高。

方法创新：

单视图深度一致性：利用单目深度估计信息，通过局部深度排名损失和深度平滑损失，约束高斯原语的深度分布，减少局部噪声，确保重建表面的连续性。

多视图特征一致性：通过多视图投影特征对深度渲染点进行优化，确保多视图间特征对齐，从而提升重建细节质量。

高效训练：无需大规模预训练或长时间逐场景优化，直接从稀疏视图输入进行快速训练和重建。

实验结果：

• 在DTU数据集（大重叠和小重叠设置）和BlendedMVS数据集上，FatesGS均取得了优于现有方法的重建精度。

• 与2DGS、NeuSurf、UFORecon等方法相比，FatesGS在细节保留和全局几何完整性方面表现更优。

• 在效率方面，FatesGS仅需14分钟即可完成训练，相比其他方法显著减少了训练时间和GPU内存占用。

论文难点

稀疏视图下的过拟合问题：稀疏输入视图导致高斯原语过拟合训练视图，产生噪声和不完整的重建表面。如何在有限视图下约束高斯原语的分布，避免过拟合，是该研究的关键难点之一。

多视图特征对齐的挑战：在稀疏视图下，多视图间特征对齐困难，因为视图数量有限且视图间隔较大，光照变化对颜色特征的影响更明显。如何设计有效的多视图特征对齐策略，以提升重建细节质量，是另一个难点。

深度一致性与细节平衡：单视图深度一致性有助于粗略几何形状的重建，但可能导致过度平滑，丢失细节。如何在深度一致性约束和细节保留之间取得平衡，是实现高质量重建的关键。

高效优化与快速训练：在保证重建精度的同时，如何实现快速训练和优化，避免大规模预训或长时间逐场景优化，是该研究面临的实际应用难题。

论文详细讲解

1. 研究背景与动机

表面重建是从多视图图像中重建三维场景表面的任务，广泛应用于计算机视觉、图形学和机器人领域。传统方法如多视图立体（MVS） 在密集视图下表现良好，但在稀疏视图下由于缺乏匹配特征而效果不佳。近年来，基于神经隐式表示（如NeRF） 的方法在密集视图重建中取得了进展，但在稀疏视图下容易过拟合，导致几何坍塌。高斯绘制（Gaussian Splatting） 因其快速训练和高质量渲染而受到关注，但在稀疏视图下仍存在几何一致性问题。

2. FatesGS方法概述

论文提出了一种名为FatesGS的稀疏视图表面重建框架，通过结合单视图深度一致性和多视图特征一致性，解决了稀疏视图下的过拟合和几何坍塌问题。具体来说，FatesGS的主要贡献包括：

• 提出了一种基于2D高斯的表面重建方法，通过单目深度信息和多视图特征对齐优化高斯原语的几何属性。

• 在稀疏视图下实现了快速训练，无需大规模预训练或长时间逐场景优化。

• 在DTU和BlendedMVS数据集上验证了方法的有效性，显著提升了重建精度和速度。

3. 方法细节

3.1 单视图深度一致性

单视图深度一致性通过局部深度排名损失和深度平滑损失实现：

• 局部深度排名损失：将图像划分为大小为\(M \times M\)的块，对每个块内的像素进行随机打乱，然后计算渲染深度和单目深度之间的排名一致性。损失函数定义为：

\[L_r = \sum_{i,j} \sigma \left( \text{sgn} \left( \hat{D}_{i,j} - \hat{D}_{i,k} \right) \cdot \left( D_{i,j} - D_{i,k} \right) + m \right)\]

其中，\(\hat{D}\)为渲染深度，\(D\)为单目深度，\(\sigma\)为ReLU函数，\(m\)为小正阈值。

• 深度平滑损失：用于减少纹理缺失区域的深度突变，增强重建表面的连续性。损失函数定义为：

\[L_s = \sum_{i,j,k} \sigma \left( \left| \hat{D}_{i,j} - \hat{D}_{k} \right| - m_t \right)\]

其中，\(k\)为相邻像素，\(m_t\)为阈值。

3.2 多视图特征一致性

多视图特征一致性通过多级特征投影损失实现：

• 对于每个像素，计算其在其他视图中的投影特征，并通过特征一致性约束优化几何细节。损失函数定义为：

\[L_f = \sum_{s,i,l} \frac{1}{l} \cdot v_{r,s,i} \left( 1 - \cos \left( F^l_r(p_{r,i}), F^l_s(p_{s,i}) \right) \right)\]

其中，\(F^l\)为特征提取网络的输出，\(v_{r,s,i}\)为可见性项，用于判断投影点是否被遮挡。

3.3 总体损失函数

FatesGS的总体损失函数结合了颜色损失、深度一致性损失和多视图特征一致性损失：

\[L = L_c + \lambda_1 L_r + \lambda_2 L_s + \lambda_3 L_f + \lambda_4 L_d + \lambda_5 L_n\]

其中，\(L_c\)为颜色损失，\(L_d\)和\(L_n\)分别为深度失真损失和法线一致性损失，\(\lambda_i\)为权重系数。

4. 实验与结果

4.1 数据集与设置

• 数据集：使用DTU数据集（15个场景，每个场景包含49或69张图像）和BlendedMVS数据集进行验证。

• 设置：在DTU数据集上，分别测试了大重叠（SparseNeuS设置）和小重叠（PixelNeRF设置）两种稀疏视图场景。

4.2 与现有方法的比较

• 重建精度：FatesGS在DTU数据集上的平均Chamfer Distance（CD）为0.92，在BlendedMVS数据集上表现出色，显著优于2DGS、NeuSurf、UFORecon等方法。

• 训练效率：FatesGS仅需14分钟即可完成训练，相比其他方法（如SparseNeuSft需2.5天预训练，NeuSurf需14小时逐场景优化）显著提升了训练速度。

• 深度预测：在DTU数据集上，FatesGS的深度预测误差显著低于Marigold和2DGS，验证了其在多视图深度学习中的优势。

4.3 消融研究

• 各模块的有效性：通过移除单视图深度一致性损失（\(L_r\)）、深度平滑损失（\(L_s\)）和多视图特征一致性损失（\(L_f\)），验证了各模块对重建精度的贡献。结果表明，多视图特征一致性损失对细节重建至关重要。

• 视图数量的影响：随着输入视图数量的增加，重建精度逐步提升，验证了多视图一致性对稀疏视图重建的重要性。

5. 结论

FatesGS通过结合单视图深度一致性和多视图特征一致性，在稀疏视图下实现了快速且高质量的表面重建。该方法无需大规模预训练或长时间逐场景优化，具有较高的实用性和效率。实验结果表明，FatesGS在DTU和BlendedMVS数据集上均取得了优于现有方法的性能，为稀疏视图重建领域提供了新的解决方案。

论文方法部分详细讲解

1. 方法概述

论文提出了一种名为 FatesGS 的稀疏视图表面重建方法，基于 Gaussian Splatting 管道，并引入了单视图深度一致性和多视图特征一致性两个约束条件，以提高稀疏视图下的重建精度和速度。

2. Gaussian Splatting基础

Gaussian Splatting 是一种通过显式高斯原语表示场景的方法，能够实现高质量渲染和快速训练。每个高斯原语由中心位置 \(\mu\)、缩放矩阵 \(S\)、旋转矩阵 \(R\)、透明度 \(o\) 和球谐系数（SH）定义。通过局部仿射变换和 alpha 融合技术，可以渲染出视图相关的外观。

为了更好地表示物体表面，论文将 3D 高斯椭球体简化为 2D 高斯椭圆，其在世界空间中的局部切平面上定义为：

\[P(u, v) = \mu + s_1 t_1 u + s_2 t_2 v\]

其中，\(S = (s_1, s_2)\) 和 \(R = (t_1, t_2, t_1 \times t_2)\) 分别是缩放矩阵和旋转矩阵。

3. 单视图深度一致性

单视图深度一致性通过局部深度排名损失和深度平滑损失实现，以减少局部噪声并保留粗略几何结构。

• 局部深度排名损失：将图像划分为大小为 \(M \times M\) 的块，对每个块内的像素进行随机打乱，然后计算渲染深度 \(\hat{D}\) 和单目深度 \(D\) 的排名一致性。损失函数定义为：

\[L_r = \sum_{i,j} \sigma \left( \text{sgn} \left( D_{i,j} - D_{i,k} \right) \cdot \left( \hat{D}_{i,j} - \hat{D}_{i,k} \right) + m \right)\]

其中，\(\sigma\) 是 ReLU 函数，\(m\) 是一个小正阈值，用于避免过拟合。

• 深度平滑损失：用于减少纹理缺失区域的深度突变，增强重建表面的连续性。损失函数定义为：

\[L_s = \sum_{i,j,k} \sigma \left( \left| \hat{D}_{i,j} - \hat{D}_{k} \right| - m_t \right)\]

其中，\(k\) 表示相邻像素，\(m_t\) 是一个小正阈值，用于避免过度平滑。

4. 多视图特征一致性

多视图特征一致性通过多级特征投影损失实现，以优化重建的细节几何结构。

• 对于每个像素 \(p_{r,i}\)，计算其在其他视图中的投影特征，并通过特征一致性约束优化几何细节。损失函数定义为：

\[L_f = \sum_{s,i,l} \frac{1}{l} \cdot v_{r,s,i} \left( 1 - \cos \left( F^l_r(p_{r,i}), F^l_s(p_{s,i}) \right) \right)\]

其中，\(F^l\) 是特征提取网络的输出，\(v_{r,s,i}\) 是可见性项，用于判断投影点是否被遮挡。

5. 总体损失函数

FatesGS 的总体损失函数结合了颜色损失、深度一致性损失和多视图特征一致性损失：

\[L = L_c + \lambda_1 L_r + \lambda_2 L_s + \lambda_3 L_f + \lambda_4 L_d + \lambda_5 L_n\]

其中：

• \(L_c\) 是颜色损失，用于监督渲染颜色；

• \(L_d\) 和 \(L_n\) 分别是深度失真损失和法线一致性损失，用于优化表面几何；

• \(\lambda_i\) 是权重系数，用于平衡不同损失项。

6. 方法优势

• 快速训练：通过引入单视图深度一致性和多视图特征一致性，避免了大规模预训练或长时间逐场景优化。

• 高质量重建：结合局部深度排名损失和多视图特征对齐，有效解决了稀疏视图下的过拟合和几何坍塌问题。

• 高效优化：利用 2D 高斯简化表示，减少了计算复杂度，同时保持了高质量的重建结果。

通过上述方法，FatesGS 在稀疏视图表面重建任务中实现了快速且高精度的重建效果。

原文翻译

FatesGS：利用深度特征一致性的高斯绘制实现快速且准确的稀疏视图表面重建

黄汉，吴宇伦，邓超，高戈†，顾明，刘雨辰

1北京信息科学与技术国家研究中心（BNRist），清华大学，北京，中国

2清华大学软件学院，北京，中国

{h-huang20, wu-yl22, dengc23}@mails.tsinghua.edu.cn, {gaoge, guming, liuyushen}@tsinghua.edu.cn

摘要

最近，高斯绘制（Gaussian Splatting）在计算机视觉领域引发了新的趋势。除了用于新视图合成外，它还被扩展到多视图重建领域。最新方法在确保快速训练速度的同时，能够实现完整且详细的表面重建。然而，这些方法仍然需要密集的输入视图，其输出质量在稀疏视图下显著下降。我们观察到，高斯原语倾向于过拟合少量训练视图，导致重建表面出现噪声漂浮物和不完整。在本文中，我们提出了一种创新的稀疏视图重建框架，通过利用单视图深度信息和多视图特征一致性，实现了极为准确的表面重建。具体来说，我们利用单目深度排名信息来监督块内深度分布的一致性，并采用平滑损失来增强分布的连续性。为了实现更精细的表面重建，我们通过多视图投影特征优化深度的绝对位置。在DTU和BlendedMVS数据集上的大量实验表明，我们的方法比现有最先进方法快60到200倍，能够在无需昂贵预训练的情况下实现快速且精细的网格重建。

引言

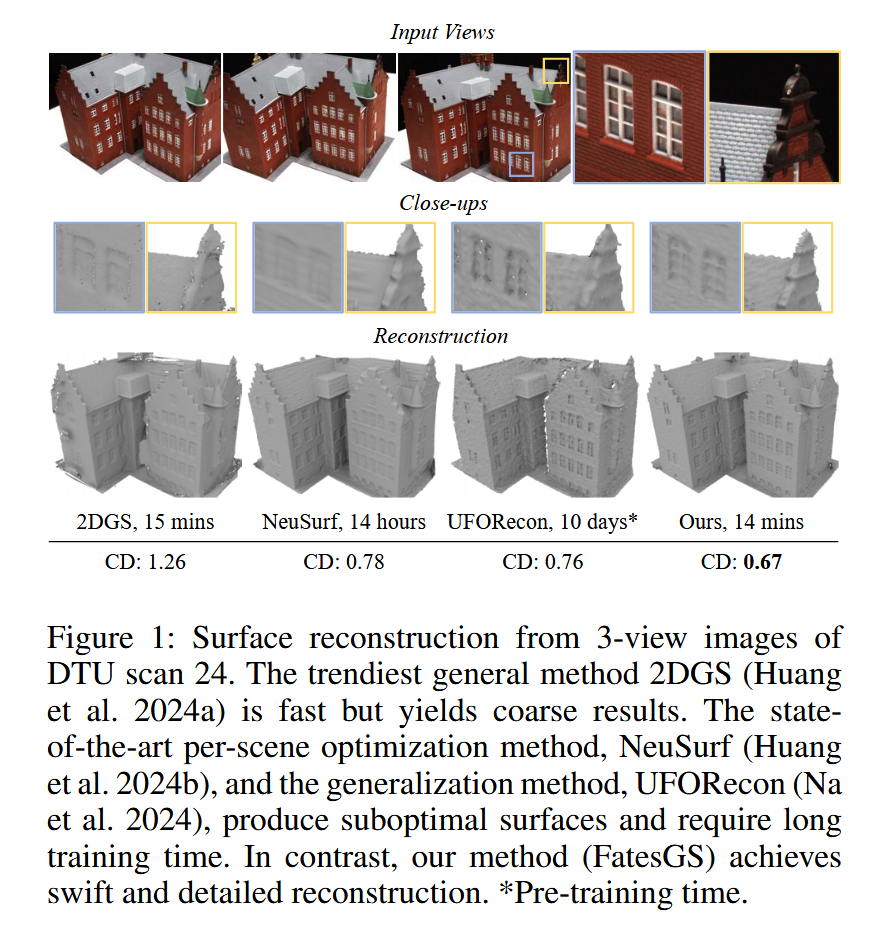
图1：从DTU扫描24的三视角图像进行表面重建。最新的通用方法2DGS（Huang等人，2024a）速度快，但结果粗糙。最先进的逐场景优化方法NeuSurf（Huang等人，2024b）以及泛化方法UFOReccon（Na等人，2024）生成的表面并非最优，且需要较长的训练时间。相比之下，我们的方法（FatesGS）实现了快速且细致的重建。*预训练时间。

从多视图图像中重建表面是3D视觉、图形学和机器人学中的一个长期任务[Ramon et al. 2021][Chen et al. 2024][Zhang, Liu, and Han 2024]。多视图立体（MVS）[Scho ̈nberger et al. 2016][Yao et al. 2018][Xu and Tao 2019]是一种传统的重建方法，包括特征提取、深度估计和深度融合等过程。该技术在密集视图下能够取得良好的结果，但由于缺乏匹配特征，在稀疏视图重建中表现不佳。近年来，基于神经辐射场（NeRF）[Mildenhall et al. 2020]的神经隐式重建迅速发展。一些方法[Wang et al. 2021][Yariv et al. 2021][Fu et al. 2022]利用神经渲染从多视图图像中优化隐式几何场和颜色场，能够通过隐式几何表示实现平滑且完整的表面重建。然而，隐式几何场在输入视图数量有限时容易过拟合，导致几何坍塌。为了应对这一问题，出现了两类用于稀疏视图重建的神经隐式方法：第一类是通用方法[Long et al. 2022][Ren et al. 2023][Na et al. 2024]，在大规模数据集上进行训练，然后用于推断新场景；第二类是针对每个场景的优化方法[Yu et al. 2022][Huang et al. 2024b]，无需预训练，直接拟合不同场景。尽管这两类方法都取得了令人满意的几何重建结果，但它们要么需要数天的预训练，要么需要针对每个场景进行数小时的优化，如图1所示。

最近，高斯绘制（Gaussian Splatting）[Kerbl et al. 2023]因其高质量的渲染和快速的训练速度被广泛用于新视图合成。然而，3D高斯在表示场景几何一致性方面存在不足，导致表面重建不够精确。为了确保表面对齐特性，一些方法[Huang et al. 2024a][Dai et al. 2024][Turkulainen et al. 2024]通过修改高斯原语的形状和绘制技术来解决这一问题。通过深度图融合，可以完整且精确地重建物体的几何形状。这些方法保留了高斯绘制在多视图重建中的快速训练速度。然而，当输入视图较少时，几何一致性降低，导致高斯原语定位不准确，深度渲染存在缺陷，进而产生噪声和不完整的输出网格。在本文中，我们提出了一个新颖的稀疏视图重建框架，通过利用高斯绘制的高效管道以及两个一致性约束来提高重建的速度和精度。具体来说，我们将3D椭球高斯转换为2D椭圆高斯，以实现更精确的几何表示，并采用2D高斯绘制来优化高斯原语的属性。为了减少过拟合引起的局部噪声，我们将图像分割成块，并利用单目深度信息来调节这些块内的排名关系。此外，我们引入平滑损失来解决纹理缺失区域的深度突变问题，从而确保深度分布的连续性。单视图深度一致性有助于实现粗略的几何重建，但会丢失许多细节。为了克服过度平滑的问题，我们对深度渲染点的重投影特征进行对齐，以确保精确的多视图特征一致性，从而显著提高表面重建的质量。我们的贡献总结如下：

• 我们提出了用于稀疏视图表面重建的FatesGS，充分利用了高斯绘制管道。与以往方法相比，我们的方法既不需要长期的逐场景优化，也不需要昂贵的预训练。

• 我们利用单视图深度一致性来促进粗略几何的学习，并进一步优化深度渲染点的多视图特征一致性以增强细节几何的学习。

• 我们在广泛使用的DTU和BlendedMVS数据集上，在两种不同的设置下，实现了稀疏视图表面重建的最新水平。

相关工作

多视图立体（MVS）

在3D重建领域，MVS方法因其可扩展性、鲁棒性和准确性而被广泛应用[Lhuillier and Quan 2005][Furukawa and Ponce 2010]。点云[Lhuillier and Quan 2005][Furukawa and Ponce 2010]、深度图[Galliani, Lasinger, and Schindler 2015][Scho ̈nberger et al. 2016][Xu and Tao 2019]和体素网格[Kostrikov, Horbert, and Leibe 2014][Ji et al. 2017][Choe et al. 2021]被用作MVS流程中的3D表示，以完成几何重建。尽管这些方法能够实现密集重建，但在纹理缺失区域通常效果有限。

神经隐式重建

NeRF（神经辐射场）[Mildenhall et al. 2020]将场景表示为密度和辐射场，并通过体积渲染进行优化。受此启发，NeuS[Wang et al. 2021]、VolSDF[Yariv et al. 2021]以及后续的优化方法[Yu et al. 2022][Fu et al. 2022][Darmon et al. 2022][Li et al. 2023]将符号距离函数（SDF）转化为密度，将多视图图像重建为隐式表面。然而，这些方法专注于密集视图重建，对输入要求较高。为了实现稀疏视图重建，最近提出了通用化方法和逐场景优化方法。通用化方法[Long et al. 2022][Ren et al. 2023][Xu et al. 2023][Peng et al. 2023][Liang, He, and Chen 2024][Na et al. 2024]在大规模数据集上训练，然后推广到新场景。这些方法需要在高性能GPU上花费大量时间（通常为数天），以提前学习3D几何与2D视图之间的对应关系。相比之下，逐场景优化方法[Yu et al. 2022][Vora, Patil, and Zhang 2023][Wang et al. 2023][Somraj and Soundararajan 2023][Somraj, Karanayil, and Soundararajan 2023][Huang et al. 2024b]不需要在大规模数据集上训练，而是直接拟合给定场景的稀疏图像的3D几何。由于缺乏学习到的对应关系，这些方法通常需要从头开始拟合数小时。

高斯绘制（Gaussian Splatting）

3D高斯绘制（3DGS）[Kerbl et al. 2023]是新视图合成领域的最新进展，利用显式的高斯原语表示场景。通过整合绘制渲染流程，3DGS在保持高质量渲染的同时实现了实时性能。然而，3DGS仍然需要密集视图输入，并且在处理稀疏输入时倾向于过拟合训练视图。为了解决这一问题，一些研究引入了单目深度正则化[Zhu et al. 2023][Chung, Oh, and Lee 2023][Li et al. 2024][Han et al. 2024]，以约束几何关系，从而减少高斯过拟合，实现高质量渲染。最近，为了将高斯绘制的优势扩展到表面重建领域，一些工作[Chen, Li, and Lee 2023][Gue ́don and Lepetit 2023][Lyu et al. 2024]通过引入正则化项和符号距离函数（SDF）隐式场来增强表面表示，但代价是训练速度降低。2DGS[Huang et al. 2024a]和高斯表面元素[Dai et al. 2024]将3D椭球体展平为2D椭圆，以获得更稳定和一致的几何表面。尽管这些方法在密集视图下取得了令人满意的结果，但在稀疏输入下只能产生噪声和不完整的表面。

方法

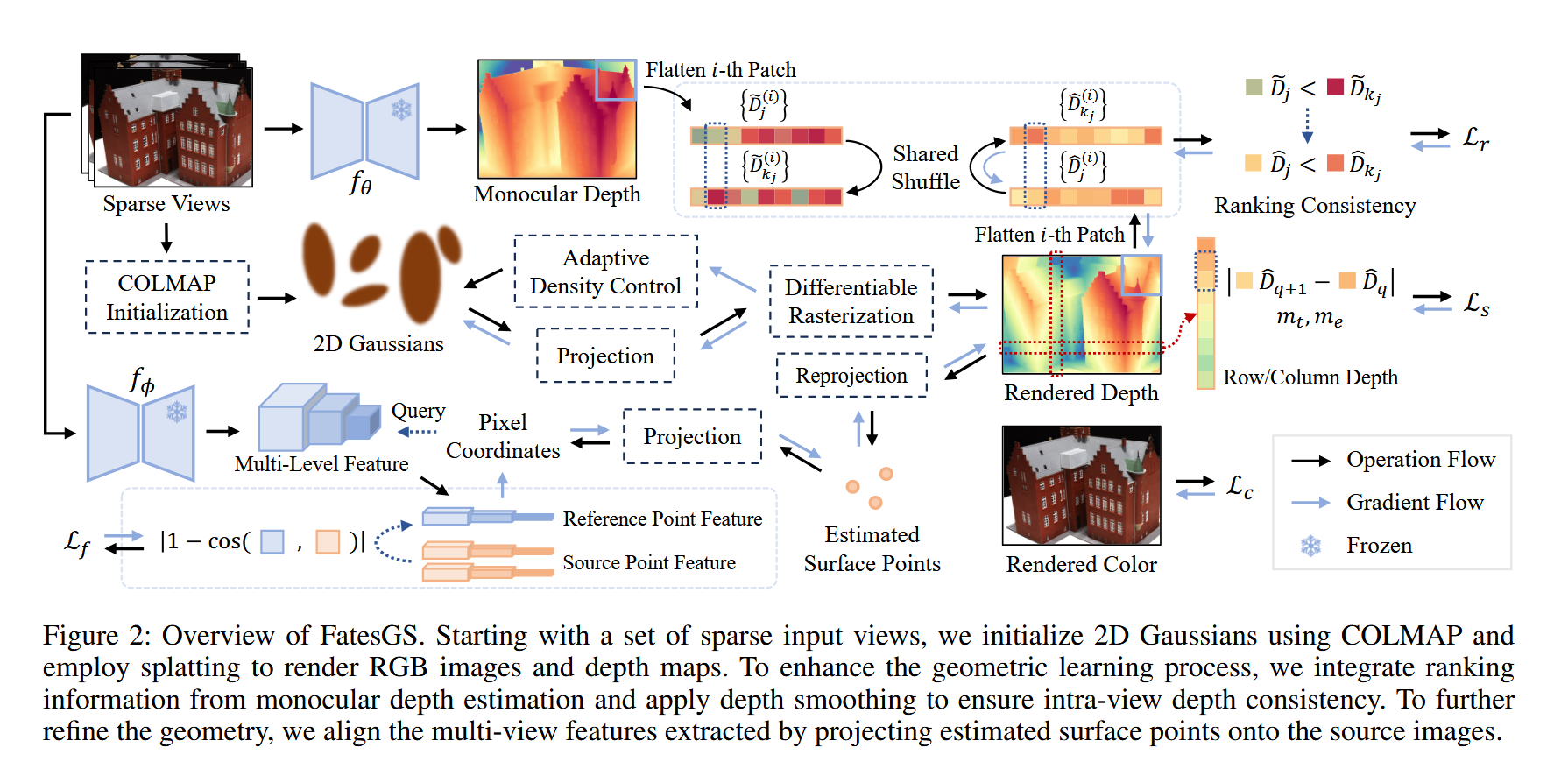
图2：FatesGS概述。从一组稀疏的输入视图开始，我们使用COLMAP初始化二维高斯分布，并采用 splatting（点溅射）技术渲染RGB图像和深度图。为了增强几何学习过程，我们整合来自单目深度估计的排序信息，并应用深度平滑处理以确保视图内的深度一致性。为了进一步优化几何形状，我们将通过将估计的表面点投影到源图像上提取的多视图特征进行对齐。

我们的目标是从一组稀疏视角图像\(\mathcal{I} = \{I_i \vert i \in 1,2\ldots,N\}\)及其位姿\(\mathcal{T} = \{T_i \vert i \in 1,2\ldots,N\}\)中重建场景的高质量几何形状\(\mathcal{S}\)。在本文中，我们提出了FatesGS，一种基于稀疏视角的高斯曲面重建方法，如图2所示。

由于高斯溅射（Gaussian splatting）过程涉及局部操作以实现快速渲染和优化，当仅提供少数视角时，它往往会产生漂浮伪影和视角不对齐问题（Sun等人，2024a）。这会导致学习到的几何形状崩溃。我们的动机是利用视图内深度一致性来防止粗略几何形状的局部噪声，并利用多视图特征对齐来保持详细几何形状的一致观测。

通过高斯溅射学习多视图几何

3DGS（Kerbl等人，2023）将场景表示为一系列三维高斯分布。每个高斯分布可以由中心位置\(\boldsymbol{\mu}\)、缩放矩阵\(S\)、旋转矩阵\(R\)、不透明度\(o\)和球谐（Spherical Harmonic，SH）系数来定义。依赖于视图的外观可以通过局部仿射变换（Zwicker等人，2001）和alpha混合技术进行渲染。尽管3DGS可以实现较好的渲染效果，但其几何结果仍然存在噪声。

遵循先前的工作（Huang等人，2024a；Dai等人，2024），我们将三维椭球体扁平化成为二维椭圆，以使基元能够更好地覆盖物体表面。缩放矩阵\(S\)和旋转矩阵\(R\)可以表示为\(S = (s_1, s_2)\)，\(R = (\boldsymbol{t}_1, \boldsymbol{t}_2, \boldsymbol{t}_1 \times \boldsymbol{t}_2)\)。然后，二维椭圆可以在世界空间中的局部切平面内定义为：

\[P(u, v) = \boldsymbol{\mu} + s_1\boldsymbol{t}_1u + s_2\boldsymbol{t}_2v. \tag{1}\]

对于\(uv\)平面内的点\(\boldsymbol{u} = (u, v)\)，其对应的二维高斯值可以使用标准高斯函数确定：

\[\mathcal{G}(\boldsymbol{u}) = \exp\left(-\frac{u^2 + v^2}{2}\right). \tag{2}\]

在场景优化过程中，二维高斯基元的参数都被设计为可学习的。依赖于视图的颜色\(\boldsymbol{c}\)通过球谐（SH）系数获得。对于高斯光栅化，二维高斯先按深度排序，然后使用alpha混合从前到后集成到图像中。对于某一图像中的一个像素，从相机发出的均匀光线\(\boldsymbol{r}\)的渲染颜色\(\hat{\boldsymbol{C}}(\boldsymbol{r})\)可以表示为：

\[\hat{\boldsymbol{C}}(\boldsymbol{r}) = \sum_{i = 1} \boldsymbol{c}_i\omega_i, \tag{3}\] \[\omega_i = o_i\mathcal{G}_i(\boldsymbol{u}(\boldsymbol{r}))\prod_{j = 1}^{i - 1}(1 - o_j\mathcal{G}_j(\boldsymbol{u}(\boldsymbol{r}))), \tag{4}\]

其中，\(\boldsymbol{c}_i\)是第\(i\)个依赖于视图的颜色，\(\omega_i\)是第\(i\)个交点的混合权重。

类似地，均匀光线\(\boldsymbol{r}\)的渲染深度\(\hat{D}(\boldsymbol{r})\)可以通过alpha混合累积为：

\[\hat{D}(\boldsymbol{r}) = \frac{\sum_{i = 1} \omega_id_i}{\sum_{i = 1} \omega_i + \epsilon}. \tag{5}\]

遵循（Huang等人，2024a），第\(i\)个交点深度\(d_i\)通过光线 - 溅射相交算法获得。

视图内深度一致性

由于高斯溅射缺乏几何场的概念，表面重建依赖于渲染深度提取。直接的深度优化似乎可以避免过拟合，并有效解决几何噪声问题。使用单目深度的绝对缩放来监督渲染深度（Yu等人，2022；Xiong等人，2023），以及增强单目深度和渲染深度之间的相关性（Zhu等人，2023），这些都被视为有效的深度正则化技术。然而，已经证明这些策略可能会导致高斯基元的噪声分布（Sun等人，2024b）。为了避免由硬约束导致的几何崩溃，我们利用单目深度信息来保持局部渲染深度的排序一致性。由于单目深度中可能存在远距离的深度歧义，我们在逐个图像块的基础上进行局部深度信息蒸馏。

具体来说，我们将图像\(I\)划分为大小均为\(M \times M\)的图像块。第\(i\)个图像块\(\mathcal{P}_i\)表示为像素列表：

\[\mathcal{P}_i = \left\{\boldsymbol{p}_j^{(i)} \big| j \in 1,\ldots,M^2\right\}. \tag{6}\]

为简化起见，对图像块中的像素进行打乱，记为：

\[\mathcal{P}_i' = \text{shuffle}(\mathcal{P}_i) = \left\{\boldsymbol{p}_{k_j}^{(i)} \big| j \in 1,\ldots,M^2\right\}. \tag{7}\]

对于\(\mathcal{P}_i\)和\(\mathcal{P}_i'\)中的每个像素，我们获取其渲染深度\(\hat{D}\)和单目深度\(\widetilde{D}\)。然后，基于图像块的深度排序损失表示为：

\[\mathcal{L}_r = \sum_{i,j} \sigma \left(\text{sgn} \left(\widetilde{D}_{k_j}^{(i)} - \widetilde{D}_{j}^{(i)}\right) \cdot \left(\hat{D}_{j}^{(i)} - \hat{D}_{k_j}^{(i)}\right) + m\right), \tag{8}\]

其中\(\sigma(\cdot)\)表示ReLU函数，\(m\)是一个小的正阈值。

基于图像块的深度排序损失确保了高斯基元的整体分布一致性。

然而，在无纹理区域中仍然存在有噪声的基元，这会导致深度突变。因此，我们提出一种针对相邻像素深度的平滑损失，以增强重建表面的分布连续性：

\[\mathcal{L}_s = \sum_{i,j,k} \sum_{\vert \widetilde{D}_k - \widetilde{D}_{(i,j)}\vert < m_e} \sigma \left(\left|\hat{D}_k - \hat{D}_{(i,j)}\right| - m_t\right). \tag{9}\]

这里，\(\hat{D}_{(i,j)}\)表示整个图像中第\(i\)行和第\(j\)列像素的渲染深度值。小的正阈值\(m_e\)和\(m_t\)用于识别边缘并避免过度平滑。\(k \in \{(i + 1, j), (i, j + 1)\}\)。

多视图特征对齐

视图内深度一致性有助于保持重建物体的整体形状和结构。虽然排序和平滑在减少伪影和保留粗略几何形状方面是有效的，但它们在细化重建的精细细节方面有所不足。多视图几何可能是一个可靠的解决方案。传统的多视图立体（MVS）重建流程通常利用多个视图之间的光度一致性来细化表面。受此启发，一个直接的想法是将每个视图深度对应的三维点投影到其他视图上，然后计算投影视图上的颜色差异。

然而，由于光照的影响，不同视点的颜色可能会有所不同（Zhan等人，2018）。当输入视图较少时，用于投影的参考视图数量有限，并且与密集视图相比，视图之间的间距更大。因此，光照对表面点颜色的影响变得更加明显。为了解决这些问题，我们设计了一个多层次特征投影损失。

令\(I_i^{(l)}\)表示从原始图像\(I_i\)按比例因子\(l\)下采样后的图像，下采样图像的集合可以标记为：

\[\mathcal{I}^{(l)} = \left\{I_i^{(l)} \big| i \in 1,2,\ldots,N\right\}, l \in 1,2,\ldots,2^L. \tag{10}\]

使用固定的特征提取网络\(f_{\phi}\)可以计算出单个层级\(l\)的多视图特征：

\[\mathcal{F}^{(l)} = f_{\phi}(\mathcal{I}^{(l)}) = \left\{\boldsymbol{F}_i^{(l)} \big| i \in 1,2,\ldots,N\right\}. \tag{11}\]

令\(I_r\)、\(I_s\)分别表示参考视图图像及其源视图图像之一。对于\(I_r\)中的像素\(\boldsymbol{p}_{r,i}\)，其渲染深度为\(\hat{D}_{r,i}\)，我们可以通过以下公式计算对应的空间点\(\boldsymbol{x}_{r,i}\)及其在源视图\(I_s\)中的投影像素坐标\(\boldsymbol{p}_{s,i}\)：

\[\begin{align} \boldsymbol{x}_{r,i} &= \boldsymbol{o}_r + \hat{D}_{r,i} \cdot \boldsymbol{d}_{r,i}, \tag{12}\\ \boldsymbol{p}_{s,i} &= K P_s^{-1} \boldsymbol{x}_{r,i}, \tag{13} \end{align}\]

其中\(K\)和\(P_s\)分别表示源视图图像\(I_s\)的内参矩阵和相机位姿。\(\boldsymbol{d}_{r,i}\)是从\(\boldsymbol{o}_r\)发出并经过\(\boldsymbol{p}_{r,i}\)的光线的归一化方向向量。然后，特征损失可以通过以下公式得到：

\[\mathcal{L}_f = \sum_{s,i,l} \frac{1}{l} \cdot v_{r,s,i} \left|1 - \cos \left(\boldsymbol{F}_r^{(l)}(\boldsymbol{p}_{r,i}), \boldsymbol{F}_s^{(l)}(\boldsymbol{p}_{s,i})\right)\right|. \tag{14}\]

由于表面点在投影到源视图时可能会被遮挡。我们设计了可见性项\(v_{r,s,i}\)，它表示从视点\(\boldsymbol{o}_s\)看\(\boldsymbol{x}_{r,i}\)的可见性。对于从\(\boldsymbol{o}_s\)发出并经过\(\boldsymbol{p}_{s,i}\)的光线\(\boldsymbol{r}_{s,i}\)上的空间点，只有最近的点被认为是可见的，其可见性项设为1，而其他点设为0。这个过程可以表示为：

\[\begin{align} v_{r,s,i} &= \left[i = \underset{t}{\arg \min} \left(\|\boldsymbol{x}_{r,t} - \boldsymbol{o}_s\|\right)\right], \tag{15}\\ \text{其中} \ t &\in \left\{t \big| \boldsymbol{p}_{s,i} = K P_s^{-1} \boldsymbol{x}_{r,t}\right\}. \end{align}\]

\([\cdot]\)表示艾弗森括号。

损失函数

总体损失函数定义如下：

\[\mathcal{L} = \mathcal{L}_c + \lambda_1\mathcal{L}_r + \lambda_2\mathcal{L}_s + \lambda_3\mathcal{L}_f + \lambda_4\mathcal{L}_d + \lambda_5\mathcal{L}_n, \tag{16}\]

其中\(\mathcal{L}_r\)和\(\mathcal{L}_s\)分别表示来自视图内深度一致性的排序损失和平滑损失，\(\mathcal{L}_f\)表示多视图特征损失。

根据3DGS（Kerbl等人，2023），\(L_1\)损失和\(L_{D - SSIM}\)损失用于颜色监督\(\mathcal{L}_c\)。其公式如下，其中\(\lambda = 0.2\)：

\[\mathcal{L}_c = (1 - \lambda)\mathcal{L}_1 + \lambda\mathcal{L}_{D - SSIM}. \tag{17}\]

与2DGS（Huang等人，2024a）一样，深度畸变损失和法向一致性损失用作正则化项来优化表面几何形状。

\[\mathcal{L}_d = \sum_{i,j} \omega_i\omega_j \vert d_i - d_j\vert , \quad \mathcal{L}_n = \sum_{i} \omega_i(1 - \boldsymbol{n}_i^T \boldsymbol{N}). \tag{18}\]

这里，\(\omega\)和\(d\)是在高斯溅射过程中计算得到的，\(\boldsymbol{n}_i^T\)表示深度点附近的估计法向量，\(\boldsymbol{N}\)是深度点附近的估计法向量。

实验与分析

为了展示我们方法的有效性和泛化性能，我们在重建精度和训练效率方面将其评估结果与以往的最新方法进行了比较。此外，我们还提供了详细的消融研究和分析，以验证我们所提方法中每个组件的有效性。

实验设置

数据集：我们在DTU数据集[Jensen et al. 2014]上评估我们的方法，该数据集在以往的表面重建研究中被广泛使用。DTU包含15个场景，每个场景包含49或69张分辨率为1600×1200的图像。我们遵循以往的研究[Huang et al. 2024b]，在大重叠（SparseNeuS）设置和小重叠（PixelNeRF）设置下，使用3个视图对模型进行训练和评估。在训练过程中，图像被缩放至800×600像素[Huang et al. 2024a]。为了评估泛化性能，我们还在BlendedMVS数据集[Yao et al. 2020]上对我们的方法进行了测试，每个场景随机选取3个输入视图，分辨率为768×576。与以往的稀疏视图设置一致，假设相机姿态是已知的。

基线方法：我们将我们的方法与多种类别的大量最新方法（SOTA）进行了比较。

i. MVS方法：COLMAP[Schonberger and Frahm 2016]和TransMVSNet[Ding et al. 2022]。

ii. 通用稀疏视图神经隐式重建方法：SparseNeuS[Long et al. 2022]、VolRecon[Ren et al. 2023]、ReTR[Liang, He, and Chen 2024]、C2F2NeuS[Xu et al. 2023]、GenS[Peng et al. 2023]和UFORecon[Na et al. 2024]。

iii. 逐场景优化神经隐式方法：NeuS[Wang et al. 2021]、VolSDF[Yariv et al. 2021]、MonoSDF[Yu et al. 2022]和NeuSurf[Huang et al. 2024b]。

iv. 基于高斯绘制的方法：3DGS[Kerbl et al. 2023]、Gaussian Surfels[Dai et al. 2024]和2DGS[Huang et al. 2024a]。为了公平比较，我们使用与我们方法相同的点云初始化3DGS和2DGS，并采用与我们相同的TSDF深度融合方法从3DGS中提取网格。

实现细节：遵循以往研究[Schonberger and Frahm 2016]，我们使用COLMAP进行高斯初始化。我们的框架基于2DGS[Huang et al. 2024a]和3DGS[Kerbl et al. 2023]构建。我们采用Vis-MVSNet[Zhang et al. 2020]作为特征提取网络\(f_\phi\)，以及Marigold[Ke et al. 2024]作为单目深度估计模型\(f_\theta\)。本文中所有实验均在单个NVIDIA RTX 3090 GPU上进行。

比较

图3：BlendedMVS数据集上三视角重建的视觉对比。

图4：DTU上不同稀疏设置下重建结果的定性对比。

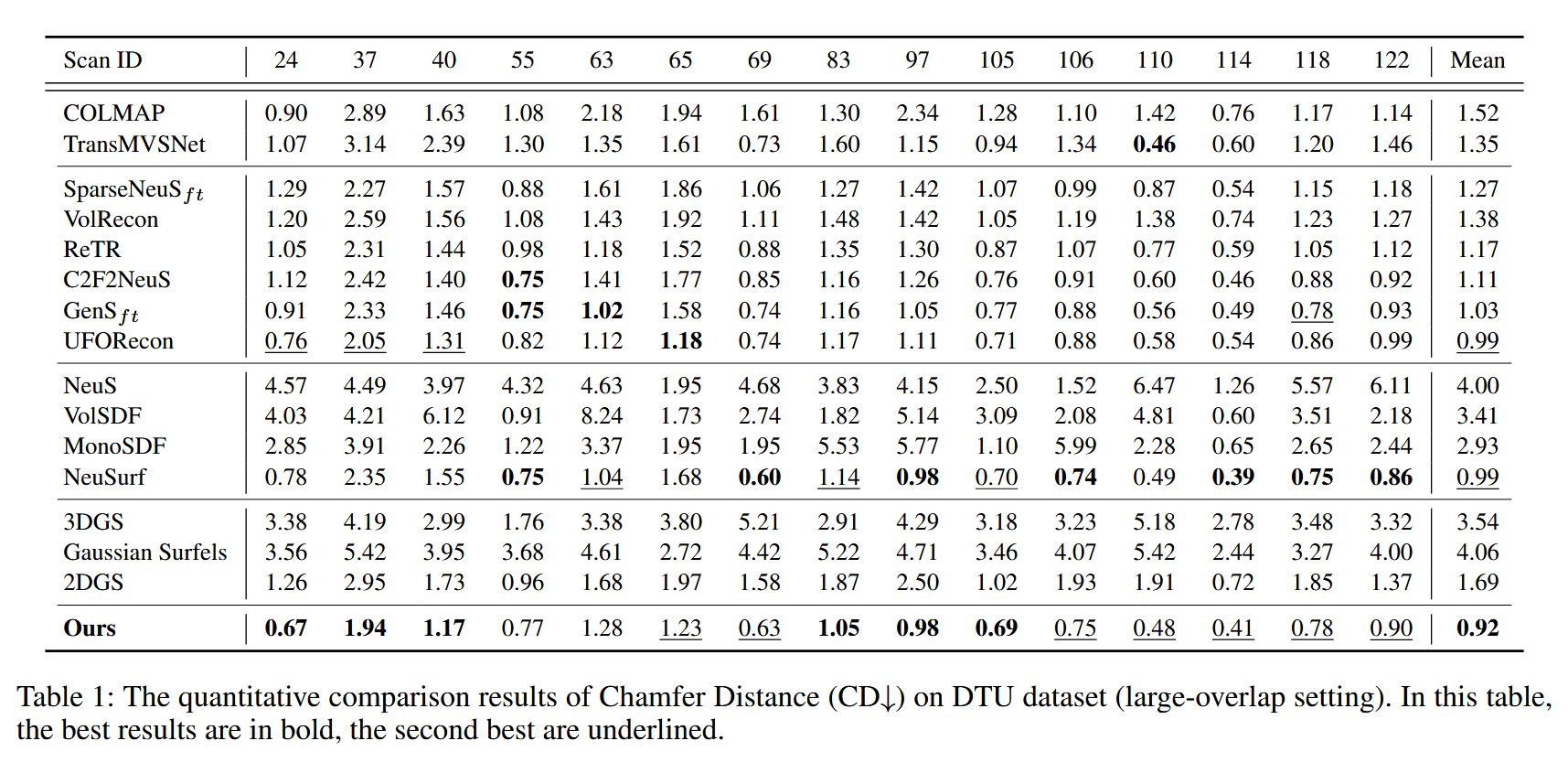
表1：DTU数据集（大重叠设置）上的倒角距离（CD↓）定量对比结果。在此表中，最佳结果以粗体显示，次佳结果以下划线标注。

稀疏视图重建：我们在DTU数据集（大重叠设置）上从稀疏输入视图进行几何重建的定量结果如表1所示。其他实验结果（例如小重叠设置）在补充材料中呈现。与其它方法相比，我们的方法在15个场景中实现了最佳的平均Chamfer距离（CD）性能。如图4所示，我们的方法实现了更全面的全局几何结构，并保留了更精细的细节。这突出了我们方法在多视图特征提取方面的优越性。此外，与NeuSurf相比，我们的方法成功避免了几何表面的过度平滑。

在BlendedMVS上的重建结果如图3所示。我们的方法在相同超参数集下，在不同数据集上展现出一致且稳定的性能。相比之下，UFORecon作为最新的通用方法，由于未在该数据集上进行广泛训练，导致重建缺陷和噪声显著。NeuSurf作为最新的逐场景优化方法，在SDF场中生成的表面过于平滑，导致局部纹理细节丢失。2DGS作为一种领先的基于高斯绘制的表面重建方法，在稀疏图像覆盖方面存在困难。几何一致性不足可能导致深度渲染有缺陷，重建结果次优。

效率

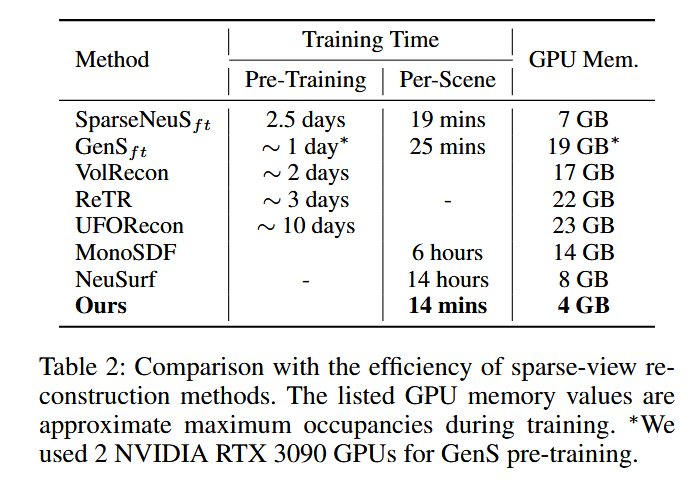
表2：稀疏视图重建方法的效率对比。列出的GPU内存值是训练期间的近似最大占用量。*我们使用2块NVIDIA RTX 3090 GPU进行GenS预训练。

我们在DTU数据集的SparseNeuS 3视图设置下对所有专门的稀疏视图重建方法进行了效率研究，具体结果如表2所示。所有结果均在单个NVIDIA RTX 3090 GPU上测试获得。为确保公平比较，所有模型均配置为优化后的最佳性能设置。在以往的方法中，通用化方法需要大量的预训练，通常耗时数天。而逐场景优化方法则需要针对每个场景进行数小时的训练。相比之下，我们的方法仅需几分钟即可完成训练，并且显著减少了GPU内存的使用。

深度预测

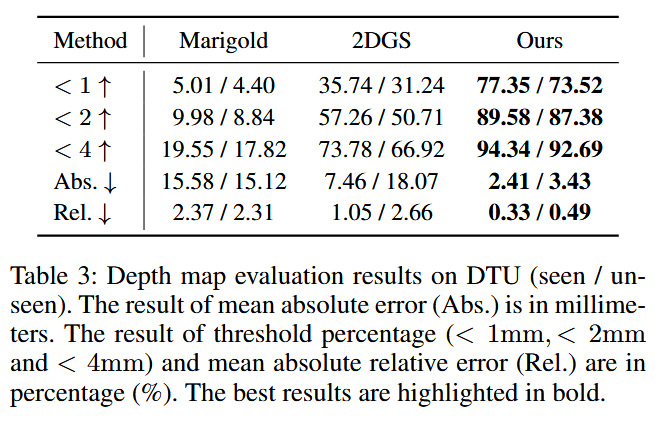
表3：DTU上的深度图评估结果（已见 / 未见数据）。平均绝对误差（Abs.）的结果以毫米为单位。阈值百分比（< 1毫米、< 2毫米和< 4毫米）以及平均绝对相对误差（Rel.）的结果以百分比（%）为单位。最佳结果以粗体突出显示。

我们使用三个已知视图对模型进行训练，并在相同的三个视图以及额外的三个未知视图上进行测试。然后，我们计算了与真实深度的误差，并将结果与Marigold[Ke et al. 2024]和2DGS[Huang et al. 2024a]方法进行了比较，如表3所示。Marigold是一种用于单目深度预测的通用方法，仅能预测相对深度。为了便于比较，我们使用真实深度将预测结果重新缩放到实际尺寸。结果显示，我们的方法在深度预测方面显著优于2D高斯绘制（2DGS）和Marigold方法。我们的方法有效地将单目深度信息与高斯绘制管道相结合，从而实现了更一致且准确的多视图深度学习。

消融研究

图5：DTU扫描83的消融研究视觉对比。误差图从蓝色到黄色的过渡表示重建误差更大。

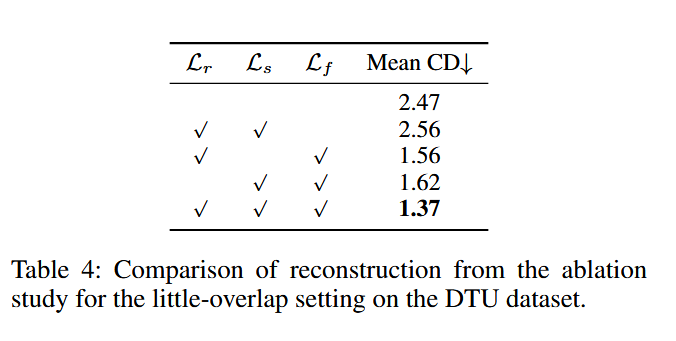
表4：DTU数据集上小重叠设置的消融研究重建对比。

所提组件的有效性：为了展示每个所提组件的有效性和必要性，我们将单独的设计选择进行隔离，并测量它们对重建质量的影响。我们在DTU数据集的小重叠设置下进行实验，保持与主实验相同的超参数。所有15个场景的平均Chamfer距离（CD）值如表4所示。此外，扫描83的消融结果如图5所示。移除每个所提优化损失会导致不同程度的性能下降，这证明了每个组件的有效性。值得注意的是，仅包含单视图深度排名损失（\(L_r\)）和平滑损失（\(L_s\)）的模型，其表现比不包含这三种损失的基线模型更差。这表明，这三种优化损失对完整模型的贡献既不是孤立的，也不是简单的累加。如图5所示，\(L_r\)和\(L_s\)提供了全局完整且粗略正确的几何引导，但由于缺乏绝对尺度信息，它们无法保证局部细节。在引入特征损失（\(L_f\)）后，我们观察到重建表面的细节得到了显著增强，有效地避免了过度平滑。

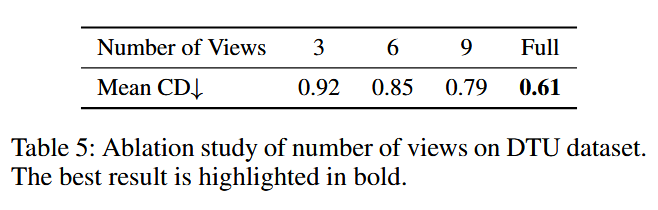
表5：DTU数据集上视图数量的消融研究。最佳结果以粗体突出显示。

训练视图数量的影响：为了验证图像数量对我们所提方法的影响，我们改变了视图的数量，结果总结在表5中。随着图像数量的增加，重建质量逐步提高。增加视图数量可以增强多视图一致性，确保稳定的重建结果，并防止过拟合。

结论

在本文中，我们提出了FatesGS，这是一种利用高斯绘制管道进行稀疏视图表面重建的新方法。为了应对稀疏视图中过拟合导致的几何坍塌问题，我们通过单视图深度一致性增强了粗略几何的学习。对于更精细的几何细节，我们优化了多视图特征一致性。我们的方法在各种稀疏设置下表现出色，且无需大规模训练。与以往方法不同，我们的方法消除了对长期逐场景优化和昂贵领域内预训练的需求。我们在广泛使用的DTU和BlendedMVS数据集上验证了我们的方法，在两种不同的设置下展示了稀疏视图表面重建的最新水平。