070, L002, k044, G053 Neural Geometric Level of Detail, Real-time Rendering with Implicit 3D Shapes

Zhangwenniu 于 2025-03-08 发布  |   阅读量: 次

论文链接

发表时间：[v1] Tue, 26 Jan 2021 18:50:22 UTC (30,627 KB)

论文重点难点讲解

论文重点

1 实时渲染神经符号距离函数（Neural SDF）

2 多细节层次（LOD）的高效表示

3 高效的渲染算法

4 实验验证

论文难点

1 八叉树与神经网络的结合

2 连续LOD的实现

3 实时渲染的优化

4 泛化能力

总结

本文通过结合稀疏体素八叉树和小尺寸MLP网络，提出了一种能够实现实时渲染的神经符号距离函数表示方法。该方法在保持高质量几何重建的同时，显著提高了渲染效率，并通过连续LOD过渡和泛化能力，展示了其在实时图形应用中的潜力。

论文详细讲解

1 研究背景与动机

神经符号距离函数（Neural SDFs）作为一种隐式3D形状表示方法，近年来在计算机图形学和计算机视觉领域受到广泛关注。传统的神经SDF通常使用大型固定尺寸的多层感知机（MLP）来近似复杂形状的隐式曲面，但这种方法在实时渲染中面临巨大挑战，因为每个像素的渲染需要多次网络前向传播，计算成本极高。本文提出了一种高效的神经表示方法，能够在保持高保真度的同时实现神经SDF的实时渲染。

2 研究方法

2.1 神经符号距离函数（Neural SDFs）

符号距离函数（SDF）是一种将空间点映射到其与目标曲面最短距离的函数，定义为：

\[f: \mathbb{R}^3 \rightarrow \mathbb{R}, \quad d = f(\mathbf{x})\]

其中，\(d\) 表示点 \(\mathbf{x}\) 到曲面 \(S\) 的符号距离，正负号表示点在曲面的内外。神经SDF通过神经网络参数化SDF，优化目标是使预测距离与真实距离尽可能接近：

\[\mathcal{L}(\theta) = \mathbb{E}_{\mathbf{x}, d} \left[ \left( f_\theta(\mathbf{x}) - d \right)^2 \right]\]

然而，直接渲染神经SDF通常需要大量的SDF评估，导致计算成本过高。

2.2 神经几何细节层次（Neural Geometric LOD）

本文提出了一种基于八叉树（octree）的特征体表示方法，结合多分辨率的细节层次（LOD），以适应不同复杂度的几何形状。具体方法如下：

1. 八叉树特征体（Octree-based Feature Volume）

使用稀疏体素八叉树（Sparse Voxel Octree, SVO）存储特征向量，每个体素的八个角点存储一个特征向量。这些特征向量可以通过一个浅层MLP解码为标量距离，从而减少计算复杂度：

\[\mathbf{z}(\mathbf{x}; L, Z) = \sum_{\ell=1}^{L} \psi(\mathbf{x}; \ell, Z)\]

其中，\(\psi(\mathbf{x}; \ell, Z)\) 是通过三线性插值计算的特征向量，\(L\) 表示LOD层次。

2. 连续LOD过渡

通过线性插值在不同离散LOD之间平滑过渡：

\[\tilde{d}_{\tilde{L}} = (1 - \alpha) d_{L^*} + \alpha d_{L^*+1}\]

其中，\(\tilde{L} = L^* + \alpha\)，\(L^*\) 是整数部分，\(\alpha\) 是小数部分。

3. 渲染算法

使用球面追踪（Sphere Tracing）算法直接渲染SDF。为了提高效率，提出了一种稀疏八叉树遍历算法，仅查询必要的LOD层次，避免在空空间中进行不必要的计算。

3 **实验与结果

3.1 几何重建质量

在多个数据集（ShapeNet、Thingi10K、TurboSquid）上验证了该方法的重建质量。与现有方法（如DeepSDF、Fourier Feature Networks、SIREN等）相比，该方法在LOD 3及以上时表现出更高的精度和更低的存储需求。例如，在TurboSquid数据集上，LOD 4的Chamfer-L1距离为\(0.069\)，显著优于其他方法。

3.2 实时渲染性能

通过不同分辨率的渲染实验，证明了该方法在实时渲染中的高效性。与DeepSDF相比，渲染速度提高了近100倍。例如，在1920×1080分辨率下，DeepSDF的帧时间为\(828\) ms，而该方法的帧时间仅为\(93\) ms。

3.3 泛化能力

该方法能够从单个形状泛化到多个形状，通过固定表面提取网络的权重，仅训练稀疏特征向量。实验表明，即使在低LOD下，该方法也能保持较高的重建质量。

3.4 几何简化

与经典的网格简化算法（如边折叠）相比，该方法在低内存预算下能够更好地保持几何细节。例如，在Thingi32数据集的狮子雕像上，该方法在LOD 3时的法线误差为\(0.023\)，显著低于网格简化方法。

4 局限性与未来工作

本文方法在训练时依赖于点样本，难以扩展到非常大的场景或薄壁几何体。此外，该方法难以使用传统方法进行动画或形变。未来的研究方向包括扩展到大规模场景、支持动画和形变，以及进一步优化渲染性能。

5 总结

本文提出了一种结合稀疏体素八叉树和小尺寸MLP的神经SDF表示方法，能够在保持高保真度的同时实现实时渲染。该方法通过多分辨率LOD和高效的渲染算法，显著提高了渲染效率，并展示了在几何重建和实时渲染中的优越性能。

论文方法部分详解

3 方法

3.1 神经符号距离函数（Neural Signed Distance Functions, SDFs）

符号距离函数（SDF）是一种隐式曲面表示方法，定义为：

\[f: \mathbb{R}^3 \to \mathbb{R}, \quad d = f(\mathbf{x})\]

其中，\(d\) 是点 \(\mathbf{x}\) 到曲面 \(S\) 的最短带符号距离，正负号表示点在曲面的内外。神经SDF通过神经网络参数化SDF，优化目标是最小化预测距离与真实距离之间的误差：

\[\mathcal{L}(\theta) = \mathbb{E}_{\mathbf{x}, d} \left[ \left( f_\theta(\mathbf{x}) - d \right)^2 \right]\]

然而，直接渲染神经SDF通常依赖于球面追踪（Sphere Tracing）算法，该算法需要对每个像素进行多次SDF评估，计算成本高昂。因此，本文提出了一种基于八叉树的特征体表示方法，以减少计算复杂度。

3.2 神经几何细节层次（Neural Geometric Levels of Detail, LOD）

本文的核心思想是将SDF表示为一个稀疏体素八叉树（Sparse Voxel Octree, SVO），并利用多分辨率的细节层次（LOD）来适应不同复杂度的几何形状。

1. 八叉树特征体（Octree-based Feature Volume）

\[\mathbf{z}(\mathbf{x}; \ell, Z) = \text{trilinear\_interp}(\mathbf{x}, \mathbf{z}^{(j)}_V)\] \[\mathbf{z}(\mathbf{x}; L, Z) = \sum_{\ell=1}^{L} \mathbf{z}(\mathbf{x}; \ell, Z)\] \[d_L = f_{\theta_L}([\mathbf{x}, \mathbf{z}(\mathbf{x}; L, Z)])\]

2. 连续LOD过渡（Continuous LOD Blending）

\[\tilde{d}_{\tilde{L}} = (1 - \alpha) d_{L^*} + \alpha d_{L^*+1}\]

其中，\(L^* = \lfloor \tilde{L} \rfloor\) 是整数部分，\(\alpha = \tilde{L} - L^*\) 是小数部分。

3. 训练（Training）

\[\mathcal{L}(\theta, Z) = \sum_{L=1}^{L_{\text{max}}} \mathbb{E}_{\mathbf{x}, d} \left[ \left( f_{\theta_L}([\mathbf{x}, \mathbf{z}(\mathbf{x}; L, Z)]) - d \right)^2 \right]\]

3.3 实时渲染（Interactive Rendering）

为了实现高效的实时渲染，本文提出了一种基于球面追踪的渲染算法，结合稀疏八叉树遍历策略，仅查询必要的LOD层次。

1. 球面追踪（Sphere Tracing）

2. 自适应光线步进（Adaptive Ray Stepping）

\[\mathbf{x}_{k+1} = \mathbf{x}_k + d_k \mathbf{d}\]

3. 稀疏光线-八叉树交检测（Sparse Ray-Octree Intersection）

def RAYTRACE_OCTREE(L, R):
    N(0) = {i, 0} for i = 0 to |R|-1
    for l = 0 to L:
        D = DECIDE(R, N(l), l)
        S = EXCLUSIVE_SUM(D)
        if l == L:
            N(l) = COMPACTIFY(N(l), D, S)
        else:
            N(l+1) = SUBDIVIDE(N(l), D, S)

4. LOD选择（LOD Selection）

\[\tilde{L} = \text{depth\_heuristic}(\text{distance\_to\_object})\]

通过上述方法，本文实现了高效的神经SDF表示和实时渲染，同时保持了高保真的几何重建质量。

原文翻译

神经几何级别细节：使用隐式3D形状的实时渲染

Towaki Takikawa\(^{1,2,4*}\) Joey Litalien\(^{1,3*}\) Kangxue Yin\(^1\) Karsten Kreis\(^1\) Charles Loop\(^1\) Derek Nowrouzezahrai\(^3\) Alec Jacobson\(^2\) Morgan McGuire\(^{1,3}\) Sanja Fidler\(^{1,2,4}\)

\(^1\)NVIDIA \(^2\)多伦多大学 \(^3\)麦吉尔大学 \(^4\)Vector研究所

nv-tlabs.github.io/nglod

摘要

神经符号距离函数(SDFs)正在成为表示3D形状的有效方法。目前最先进的方法通常使用大型固定尺寸的神经网络来编码SDF，以用隐式曲面近似复杂形状。然而，使用这些大型网络进行渲染在计算上非常昂贵，因为每个像素都需要通过网络进行多次前向传递，使这些表示方法在实时图形应用中不切实际。我们引入了一种高效的神经表示方法，首次实现了高保真神经SDF的实时渲染，同时达到了最先进的几何重建质量。我们使用基于八叉树的特征体积来表示隐式曲面，该体积可以通过多个离散细节级别(LODs)自适应拟合形状，并支持通过SDF插值实现连续LOD。我们进一步开发了一种高效算法，通过稀疏八叉树遍历仅查询必要的LOD，直接实时渲染我们的新型神经SDF表示。我们展示了我们的表示方法在渲染速度方面比之前的工作高效2-3个数量级。此外，它在3D几何和2D图像空间度量下都为复杂形状产生了最先进的重建质量。

1 引言

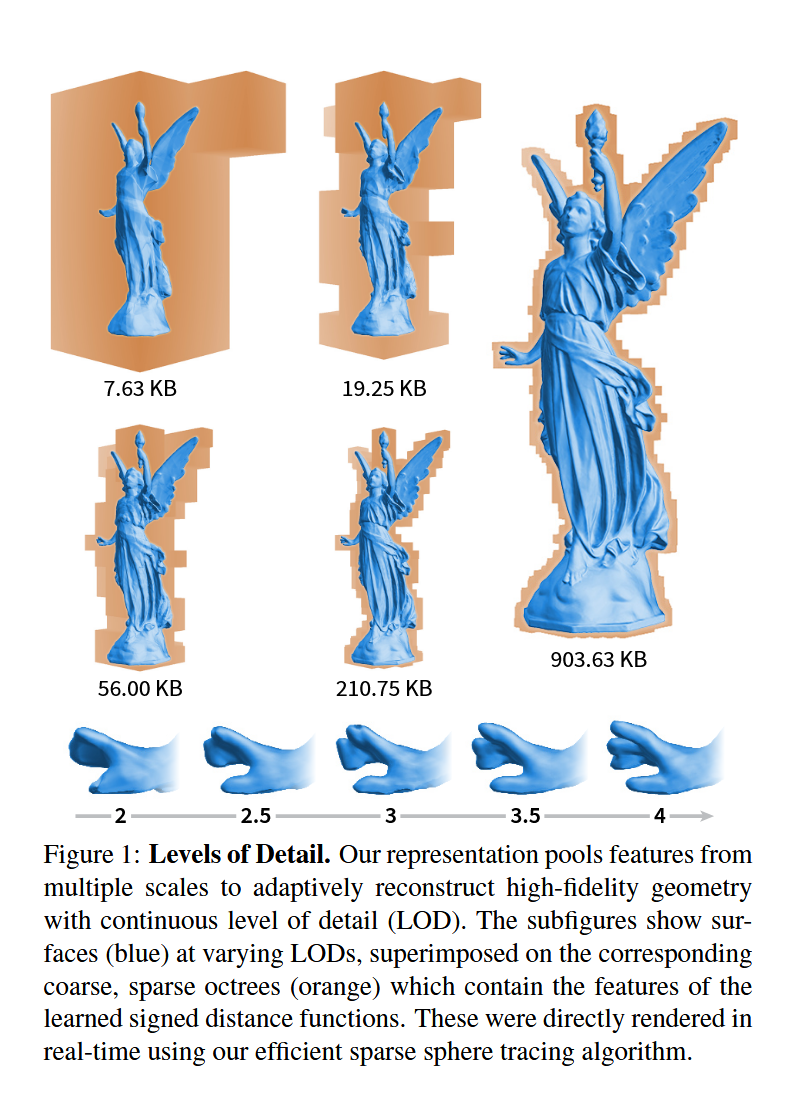
nglod.fig.1

图1：细节层次。我们的表示方法从多个尺度聚合特征，以自适应地重建具有连续细节层次（LOD）的高保真几何形状。子图展示了不同LOD下的表面（蓝色），叠加在相应的粗糙、稀疏八叉树（橙色）上，这些八叉树包含了学习到的有向距离函数的特征。这些是使用我们高效的稀疏球体追踪算法实时直接渲染的。

计算机图形学中的高级几何建模和渲染技术使用具有复杂细节、任意拓扑和高质量的3D形状，通常利用多边形网格。然而，将这些表示方法适应于基于学习的方法并不简单，因为它们缺乏可微分性，因此不能轻易地用于计算机视觉应用，如基于图像的学习型3D重建。最近，符号距离函数的神经近似（神经SDFs）已成为扩展计算机视觉和图形应用的一个有吸引力的选择。先前的工作[36, 31, 6, 8]已经表明，神经网络可以通过学习SDF来编码精确的3D几何，而不受拓扑或分辨率的限制，SDF通过其零水平集定义表面。这些工作通常使用大型、固定大小的多层感知器(MLP)作为学习的距离函数。

直接渲染和探测神经SDFs通常依赖于球体追踪[17]，这是一种寻根算法，每个像素可能需要数百次SDF评估才能收敛。由于通过大型基于MLP的SDF的单次前向传递可能需要数百万次操作，当计算单个像素的成本膨胀到数亿次操作时，神经SDFs很快就变得不适合实时图形应用。Davies等人[8]的工作通过使用小型神经网络来过拟合单个形状来规避这个问题，但这是以通用性和重建质量为代价的。先前的方法还使用固定大小的神经网络，使它们无法表达超出网络容量的复杂几何。

在本文中，我们提出了一种新型的神经SDFs表示方法，可以自适应地扩展到不同的细节级别(LODs)并重建高度详细的几何。我们的方法可以在不同尺度的几何之间平滑插值（见图1），并且可以在合理的内存占用下实时渲染。与Davies等人[8]类似，我们也使用小型MLP使球体追踪变得实用，但不牺牲质量或通用性。我们从经典的表面提取机制[26, 12]中获取灵感，这些机制使用四边形和存储距离值的空间数据结构来精细地离散化欧几里得空间，使得简单的线性基函数可以重建几何。在这些工作中，分辨率或树深度决定了几何细节级别(LOD)，不同的LODs可以通过插值进行混合。然而，它们通常需要较高的树深度才能创建出令人满意的质量解决方案。

相比之下，我们通过使用稀疏体素八叉树(SVO)来离散化空间，并且我们存储学习的特征向量而不是符号距离值。这些向量可以使用浅层MLP解码为标量距离，允许我们截断树深度，同时继承经典方法的优势（例如，LOD）。我们还开发了一种针对我们架构的光线遍历算法，使我们能够以比DeepSDF[36]快近100倍的速度渲染几何。虽然无法直接与神经体积渲染方法进行比较，但在类似的实验设置下，我们报告的帧时间比NeRF[32]快500多倍，比NSVF[24]快50倍。

总结起来，我们的贡献如下：

由于我们方法的实时性质，我们将其视为许多下游应用的模块化构建块，如基于图像的场景重建、机器人导航和形状分析。

nglod.fig.2

图2：我们能够拟合不同复杂度、风格和比例的形状，且质量始终良好，同时能够利用几何形状进行着色、环境光遮蔽[11]，甚至使用次级光线生成阴影。建议放大查看效果最佳。

2 相关工作

我们的工作与之前关于网格简化以实现细节级别、3D神经形状表示和隐式神经渲染的研究最为相关。

细节级别。计算机图形学中的细节级别(LOD)[27]指的是经过过滤以限制特征变化的3D形状，通常将特征变化限制在图像空间中像素大小的约两倍。这减轻了由混叠引起的闪烁，并通过降低模型复杂度加速渲染。虽然信号处理技术可以过滤纹理[46]，但几何过滤是特定于表示的，且具有挑战性。一种方法是网格抽取，即将网格简化为预算数量的面、顶点或边。经典方法[14, 18]贪婪地移除对几何精度影响最小的网格元素。更近期的方法针对感知度量进行优化[23, 22, 7]或专注于拓扑[29]。在低内存约束下，网格会遭受离散化误差，并且在LOD之间的混合存在困难。相比之下，SDFs可以用更少的内存表示平滑表面，并在LOD之间平滑混合以减少混叠。过去的工作[40, 44]在压缩网格SDFs方面也展示了令人印象深刻的性能。我们的神经SDFs继承了这些特性。

神经隐式表面。基于隐式表面的方法将几何编码在潜在向量或神经网络权重中，这些参数通过水平集参数化表面。开创性的工作[36, 31, 6]通过使用自动解码器将形状编码到潜在向量中来学习这些等值面——自动解码器是一个大型MLP，它输出一个以潜在向量和位置为条件的标量值。另一条并行的研究线[43, 41]使用周期函数，在重建质量上取得了很大改进。Davies等人[8]提出对单个形状过拟合神经网络，允许紧凑的MLP表示几何。像Curriculum DeepSDF[10]这样的工作在逐渐增长的网络中编码几何，但丢弃中间表示。BSPNet和CvxNet[5, 9]通过空间分割树学习隐式几何。PIFu[38, 39]在密集2D网格上学习特征，将深度作为额外的输入参数，而其他工作则在稀疏规则[15, 3, 20]或变形[13]的3D网格上学习这些特征。PatchNets[45]学习由特征点云定义的表面补丁。这些工作大多依赖于像Marching Cubes[26]这样的等值面提取算法来创建密集的表面网格以渲染对象。相比之下，本文中我们提出了一种可以直接以交互速率渲染形状的方法。

隐式表面的神经渲染。许多工作专注于渲染神经隐式表示。SRN[42]通过直接预测深度来渲染隐式表面。Niemeyer等人[34]提出了一种使用光线行进的隐式表面可微分渲染器。DIST[25]和SDFDiff[21]提出了使用球体追踪的SDF可微分渲染器。这些可微分渲染器与光线追踪算法无关；它们只需要相对于光线-表面交点的可微分性。因此，我们可以利用这些工作中提出的相同技术使我们的渲染器也具有可微分性。NeRF[32]将几何学习为密度场，并使用光线行进来可视化它们。IDR[47]将基于MLP的着色函数附加到神经SDF上，解耦几何和着色。NSVF[24]与我们的工作类似，因为它也使用稀疏八叉树编码特征表示。与NSVF相比，我们的工作支持细节级别并使用球体追踪，这使我们能够将几何与着色分离，从而优化光线追踪，这在体积渲染框架中是不可能的。如前所述，与NSVF[24]报告的数据相比，我们的渲染器快两个数量级。

3 方法

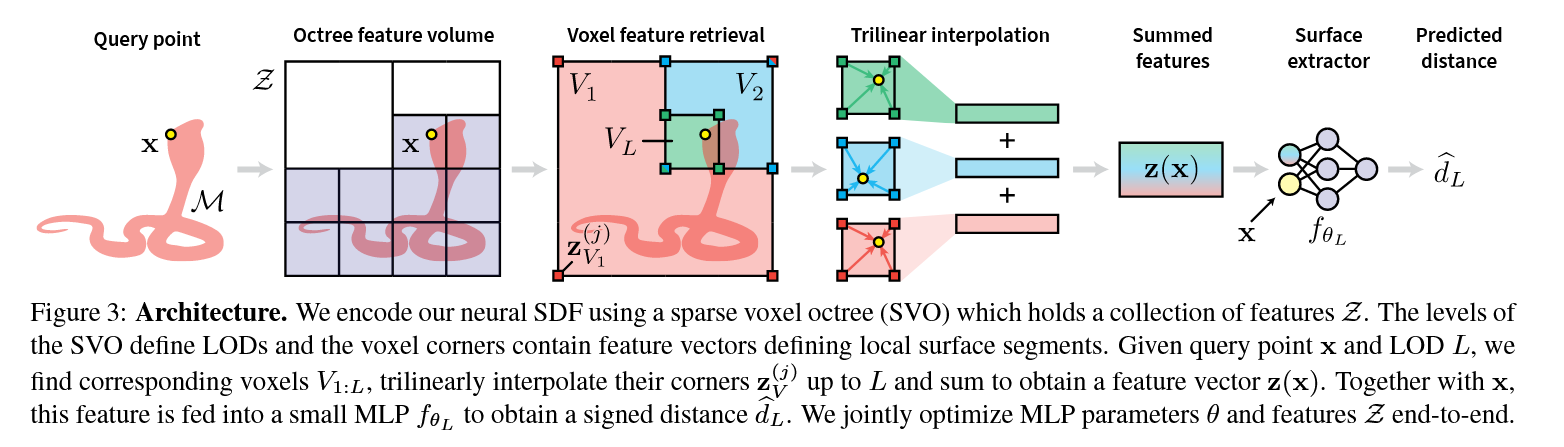
nglod.fig.3

图3：架构。我们使用一个稀疏体素八叉树（SVO）对神经有向距离函数（SDF）进行编码，该八叉树包含一组特征\(\mathcal{Z}\)。SVO的层级定义了LOD，体素角点包含定义局部表面片段的特征向量。给定查询点\(\mathbf{x}\)和LOD \(L\)，我们找到相应的体素\(V_{1:L}\)，对其角点的特征向量\(\mathbf{z}_V^{(j)}\)进行三线性插值（最高到层级\(L\)）并求和，以获得特征向量\(\mathbf{z}(\mathbf{x})\)。该特征与\(\mathbf{x}\)一起输入到一个小型多层感知机\(f_{\theta_L}\)中，以获得有向距离\(\widehat{d}_L\)。我们对MLP的参数\(\theta\)和特征\(\mathcal{Z}\)进行端到端联合优化。

我们的目标是设计一种表示方法，该方法能够重建详细的几何形状，并实现连续的细节层次，同时能够以交互式速率进行渲染。图3展示了我们方法的可视化概述。3.1节提供了神经有向距离函数（signed distance functions，SDFs）的背景知识及其局限性。然后，我们在3.2节中介绍将神经SDF编码到稀疏体素八叉树中的方法，并在3.3节中提供训练细节。针对我们的表示方法量身定制的渲染算法在3.4节中描述。

3.1 神经有向距离函数（SDFs）

nglod.fig.3.1

SDFs是函数\(f : \mathbb{R}^3 \to \mathbb{R}\)，其中\(d = f(\mathbf{x})\)是从点\(\mathbf{x}\)到体积\(\mathcal{M} \subset \mathbb{R}^3\)的表面\(\mathcal{S} = \partial\mathcal{M}\)的最短有向距离，符号表示\(\mathbf{x}\)是在\(\mathcal{M}\)内部还是外部。因此，\(\mathcal{S}\)被隐式表示为\(f\)的零水平集：

\[\mathcal{S} = \{\mathbf{x} \in \mathbb{R}^3 \vert f(\mathbf{x}) = 0\}. \tag{1}\]

神经SDF将SDF编码为神经网络\(f_{\theta}\)的参数\(\theta\)。检索点\(\mathbf{x} \in \mathbb{R}^3\)的有向距离相当于计算\(f_{\theta}(\mathbf{x}) = \hat{d}\)。参数\(\theta\)通过损失\(J(\theta) = \mathbb{E}_{\mathbf{x},d}\mathcal{L}(f_{\theta}(\mathbf{x}), d)\)进行优化，其中\(d\)是真实的有向距离，\(\mathcal{L}\)是某种距离度量，如\(L^2\)距离。一个可选的输入“形状”特征向量\(\mathbf{z} \in \mathbb{R}^m\)可用于对网络进行条件设定，以便在固定的\(\theta\)下拟合不同的形状。

为了直接渲染神经有向距离函数（SDFs），可以使用诸如球体追踪[17]之类的求根算法进行光线追踪。该算法每条光线最多可执行一百次距离查询。如果网络规模较大且距离查询速度过慢，那么标准的神经SDFs 的计算成本将高得令人望而却步。使用小型网络可以加快这种迭代渲染过程，但重建的形状可能不准确。此外，固定大小的网络无法拟合高度复杂的形状，也无法适应简单或远距离的、无需视觉细节的物体。

在下一节中，我们将描述一个框架，该框架通过使用稀疏体素八叉树对SDF进行编码来解决这些问题，使这种表示方法能够适应不同的细节层次，并在保持几何精度的同时，使用浅层神经网络对几何形状进行编码。

3.2 神经几何细节层次

框架。与标准的神经有向距离函数（SDFs）类似，我们使用神经网络的参数以及一个额外的经过学习的输入特征来表示SDFs，该输入特征对形状进行编码。与DeepSDF[36]中使用单个特征向量\(\mathbf{z}\)对形状进行编码不同，我们使用一个特征体\(\mathcal{Z}\)，它包含一组特征向量。

我们将\(\mathcal{Z}\)存储在一个跨越包围体\(\mathcal{B} = [-1, 1]^3\)的稀疏体素八叉树（SVO）中。SVO中的每个体素\(V\)在其八个角点（由\(j\)索引）处都持有一个可学习的特征向量\(\mathbf{z}_V^{(j)} \in \mathcal{Z}\)，如果相邻体素存在，则这些特征向量是共享的。仅当体素\(V\)包含表面时才分配体素，这使得SVO是稀疏的。

SVO的每个层级\(L \in \mathbb{N}\)都为几何形状定义了一个细节层次（LOD）。随着SVO中树深度\(L\)的增加，表面的离散化程度更高，从而使重建质量能够随着内存使用量进行调整。我们将最大树深度表示为\(L_{max}\)。此外，我们为每个LOD使用小型多层感知机（MLP）神经网络\(f_{\theta_{1:L_{max}}}\)，称为解码器，其参数为\(\theta_{1:L_{max}} = \{\theta_1, \ldots, \theta_{L_{max}}\}\)。

为了在期望的LOD \(L\)下计算查询点\(\mathbf{x} \in \mathbb{R}^3\)的SDF，我们遍历树直到层级\(L\)，以找到所有包含\(\mathbf{x}\)的体素\(V_{1:L} = \{V_1, \ldots, V_L\}\)。对于每个层级\(\ell \in \{1, \ldots, L\}\)，我们通过对\(\mathbf{x}\)处体素的角点特征进行三线性插值来计算每个体素的形状向量\(\psi(\mathbf{x}; \ell, \mathcal{Z})\)。我们对各层级的特征求和，得到\(\mathbf{z}(\mathbf{x}; L, \mathcal{Z}) = \sum_{\ell=1}^{L} \psi(\mathbf{x}; \ell, \mathcal{Z})\)，并将其输入到具有LOD特定参数\(\theta_L\)的MLP中。具体来说，我们按如下方式计算SDF：

\[\widehat{d}_L = f_{\theta_L}([\mathbf{x}, \mathbf{z}(\mathbf{x}; L, \mathcal{Z})]), \tag{2}\]

其中\([\cdot, \cdot]\)表示连接操作。这种跨LOD的求和允许有意义的梯度在各LOD之间传播，尤其对较粗糙的LOD有帮助。

由于我们的形状向量\(\mathbf{z}_V^{(j)}\)现在仅表示小的表面片段，而不是整个形状，我们可以将计算复杂度从神经网络\(f_{\theta}\)转移到特征向量查询\(\psi : \mathbb{R}^3 \to \mathbb{R}^m\)中，这相当于进行SVO遍历以及对体素特征进行三线性插值。这一关键设计决策使我们能够使用非常小的MLP，在不牺牲重建质量的前提下实现显著的加速。

层级混合

尽管八叉树的层级是离散的，但我们能够在它们之间进行平滑插值。为了获得期望的连续细节层次（LOD）\(\widetilde{L} \geq 1\)，我们通过对不同离散八叉树LOD \(L\) 对应的预测距离进行线性插值来混合：

\[\widehat{d}_{\widetilde{L}} = (1 - \alpha) \widehat{d}_{L^*} + \alpha \widehat{d}_{L^* + 1}, \tag{3}\]

其中\(L^* = \lfloor\widetilde{L}\rfloor\) ，\(\alpha = \widetilde{L} - \lfloor\widetilde{L}\rfloor\) 是小数部分，这使我们能够在LOD之间平滑过渡（见图1）。这种简单的混合方案仅适用于SDF，对于密度或占有率效果不佳，并且对于网格和点云没有定义。我们将在3.4节中讨论在渲染时如何设置连续LOD \(\widetilde{L}\)。

3.3 训练

我们通过联合训练每个LOD，确保稀疏体素八叉树（SVO）的每个离散层级\(L\)都表示有效的几何形状。我们通过计算每个层级的单独损失并将它们在各层级上求和来实现这一点：

\[J(\theta, \mathcal{Z}) = \mathbb{E}_{\mathbf{x},d} \sum_{L = 1}^{L_{max}} \left\|f_{\theta_L}([\mathbf{x}, \mathbf{z}(\mathbf{x}; L, \mathcal{Z})]) - d\right\|^2. \tag{4}\]

然后，我们针对\(\theta_{1:L_{max}}\)和\(\mathcal{Z}\)对损失函数进行随机优化。对于点\(\mathbf{x} \in \mathcal{B}\)，通过重要性采样来估计期望。我们使用来自三种分布混合的样本：\(\mathcal{B}\)中的均匀样本、表面样本和扰动后的表面样本。我们在补充材料中详细介绍了这些采样算法和具体的训练超参数。

3.4 交互式渲染

球体追踪。我们使用球体追踪[17]直接渲染我们的表示。然而，使用球体追踪渲染基于稀疏体素八叉树（SVO）的有向距离函数（SDF）会带来一些需要解决的技术问题。典型的SDF在整个\(\mathbb{R}^3\)上定义。相比之下，我们的SVO SDF仅为与表面几何形状相交的体素\(V\)定义。因此，需要妥善处理在空白空间中进行的距离查询。一种选择是使用固定步长，即光线步进，但不能保证追踪会收敛，因为步长可能过大。

相反，在帧开始时，我们首先执行光线 - SVO相交操作（细节如下），以检索每个分辨率\(\ell\)下与光线相交的每个体素\(V\)。形式上，如果\(\mathbf{r}(t) = \mathbf{x}_0 + t\mathbf{d}, t > 0\)是一条起点为\(\mathbf{x}_0 \in \mathbb{R}^3\)、方向为\(\mathbf{d} \in \mathbb{R}^3\)的光线，我们令\(\mathcal{V}_{\ell}(\mathbf{r})\)表示在层级\(\ell\)下与\(\mathbf{r}\)相交的按深度排序的体素集合。

\(\mathcal{V}_{\ell}(\mathbf{r})\)中的每个体素包含相交光线的索引、体素位置、父体素以及指向八个角点特征向量\(\mathbf{z}_V^{(j)}\)的指针。为了节省内存，我们检索指针而不是特征向量。特征向量存储在一个扁平数组中，并且指针在初始化步骤中通过遍历所有体素并找到每个角点特征的相应索引来预先计算。

自适应光线步进。对于球体追踪迭代\(k\)中的给定光线，我们对目标LOD层级\(L\)的体素执行光线 - 轴对齐包围盒（AABB）相交操作[28]，以检索第一个命中的体素\(V_L^* \in \mathcal{V}_L(\mathbf{r})\)。如果\(\mathbf{x}_k \notin V_L^*\)，我们将\(\mathbf{x}\)推进到光线 - AABB相交点。如果\(\mathbf{x}_k \in V_L^*\)，我们查询特征体。我们递归地检索对应于较粗糙层级\(\ell \in \{1, \ldots, L - 1\}\)的所有父体素\(V_{\ell}^*\)，从而得到一组体素\(V_{1:L}^*\)。然后，我们对每个节点处的三线性插值特征求和。注意，根据构造，父节点总是存在的。然后，多层感知机\(f_{\theta_L}\)生成一个保守距离\(\widehat{d}_L\)，用于沿方向\(\mathbf{d}\)移动，我们执行标准的球体追踪步骤：\(\mathbf{x}_{k + 1} \leftarrow \mathbf{x}_k + \widehat{d}_L\mathbf{d}\)。

如果\(\mathbf{x}_{k + 1}\)现在处于空白空间中，我们跳到沿光线\(\mathcal{V}_L(\mathbf{r})\)中的下一个体素，如果不存在则丢弃光线\(\mathbf{r}\)。如果\(\mathbf{x}_{k + 1}\)在一个体素内，我们执行一个球体追踪步骤。这个过程会一直重复，直到所有光线都未命中，或者达到停止条件以找到一个命中点\(\mathbf{x}^* \in \mathcal{S}\)。图4展示了这个过程。这种自适应步进通过无需在空白空间中查询来实现体素稀疏性，使我们的表示所需的存储最小化。我们在补充材料中详细说明了停止条件。

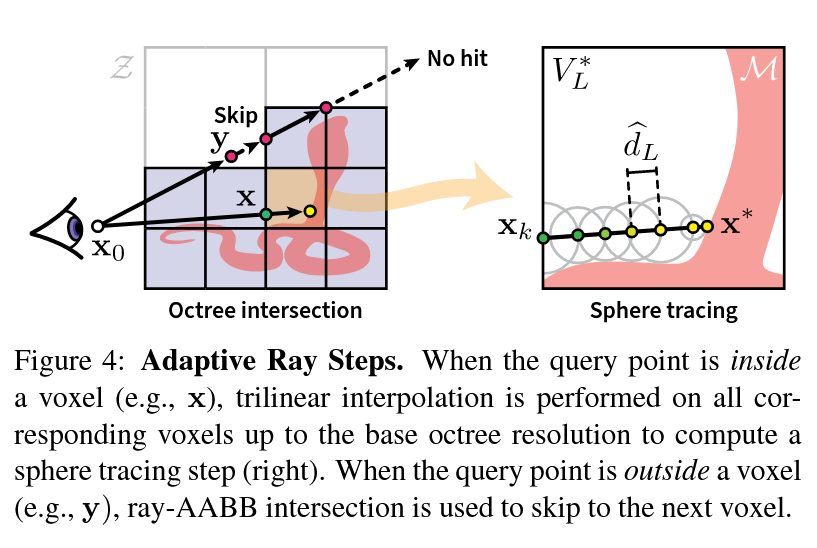
nglod.fig.4

图4：自适应光线步进。当查询点在体素内部（例如，\(\mathbf{x}\)）时，对直至基础八叉树分辨率的所有相应体素进行三线性插值，以计算一个球体追踪步长（右图）。当查询点在体素外部（例如，\(\mathbf{y}\)）时，使用光线 - 轴对齐包围盒（AABB）相交来跳到下一个体素。

稀疏光线 - 八叉树相交。现在我们描述我们新颖的光线 - 八叉树相交算法，该算法使用广度优先遍历策略和并行扫描内核[30]，以在现代图形硬件上实现高性能。算法1提供了我们算法的伪代码。我们在补充材料中提供了子例程的详细信息。

nglod.alg.1

该算法首先生成一组光线\(\mathcal{R}\)（由\(i\)索引），并将它们存储在一个光线 - 体素对的数组\(\mathbf{N}^{(0)}\)中，这些是光线 - 体素相交的待选对象。我们用根节点，即八叉树的顶级体素初始化每个\(\mathbf{N}_i^{(0)} \in \mathbf{N}^{(0)}\)（第2行）。接下来，我们遍历八叉树的层级\(\ell\)（第3行）。在每次迭代中，我们在DECIDE函数中确定产生相交的光线 - 体素对，该函数返回一个决策列表\(\mathbf{D}\)，如果光线与体素相交，则\(\mathbf{D}_j = 1\)，否则\(\mathbf{D}_j = 0\)（第4行）。然后，我们使用EXCLUSIVESUM计算列表\(\mathbf{D}\)的前缀和\(\mathbf{S}\)，并将其输入到接下来的两个子例程中（第5行）。如果我们还没有达到期望的LOD层级\(L\)，我们使用SUBDIVIDE用光线相交的那些\(\mathbf{N}_j^{(\ell)}\)的子体素填充下一个列表\(\mathbf{N}^{(\ell + 1)}\)，并继续迭代（第9行）。否则，我们使用COMPACTIFY移除所有不产生相交的\(\mathbf{N}_j^{(\ell)}\)（第7行）。结果是八叉树每个层级的一个紧凑的、按深度排序的光线 - 体素相交列表。注意，通过分析光线起点在体素内所处的卦限，我们可以对子体素进行排序，使得光线 - 体素对列表\(\mathbf{N}^{(L)}\)将按与光线起点的距离排序。

LOD选择。我们使用深度启发式方法选择用于渲染的LOD \(\widetilde{L}\)，其中\(\widetilde{L}\)根据与对象的距离，在用户定义的阈值之间线性过渡。存在更严谨的方法[2]，但我们将细节留给用户，让他们选择最适合自己需求的算法。

4 实验

我们进行了几项实验来展示我们架构的有效性。我们首先将我们的模型拟合到来自ShapeNet[4]、Thingi10K[48]和TurboSquid\(^1\)精选模型等数据集的3D网格模型，并基于3D几何度量和渲染图像空间度量进行评估。我们还证明了我们的模型能够拟合来自Shadertoy\(^2\)具有独特属性的复杂解析符号距离函数。此外，我们展示了实时渲染、对多个形状的泛化和几何简化的结果。我们实验中使用的MLP仅有一个隐藏层，维度\(h = 128\)，中间层使用ReLU激活函数，因此比我们比较的基准模型中使用的网络小得多且运行更快，如我们的实验所示。我们使用SVO特征维度\(m = 32\)。我们使用高斯先验初始化体素特征\(z \in Z\)，其中\(\sigma = 0.01\)。

4.1 重建3D数据集

我们在几个不同的3D数据集上拟合我们的架构，以评估重建表面的质量。我们与包括DeepSDF[36]、傅里叶特征网络[43]、SIREN[41]和神经隐式(NI)[8]在内的基准进行比较。这些架构在过拟合3D形状方面表现出最先进的性能，并且有源代码可用。我们尽最大努力使用他们的源代码作为参考重新实现这些基准，并在补充材料中提供详细信息。

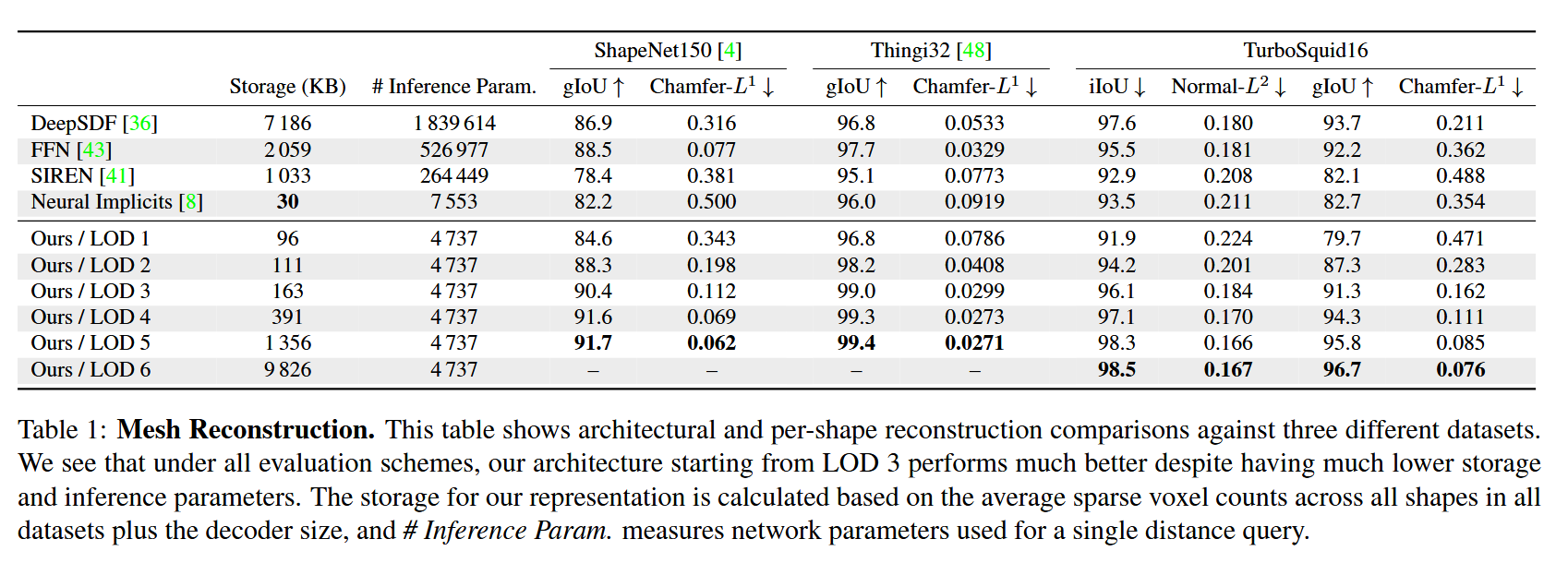
nglod.table.1

表1：网格重建。此表展示了针对三个不同数据集的架构和单个形状重建的比较。我们可以看到，在所有评估方案下，尽管我们的架构从LOD 3开始，其存储和推理参数要低得多，但性能却好得多。我们表示方法的存储是根据所有数据集中所有形状的平均稀疏体素数量加上解码器大小来计算的，“推理参数数量（# Inference Param.）”衡量用于单次距离查询的网络参数。

网格数据集。表1显示了ShapeNet、Thingi10K和TurboSquid的总体结果。我们分别从每个数据集中抽取150、32和16个形状，并分别使用100、100和600个周期对每个形状进行过拟合。对于ShapeNet150，我们使用汽车、飞机和椅子类别中各50个形状。对于Thingi32，我们使用32个标记为扫描的形状。ShapeNet150和Thingi32使用Chamfer-L1距离（乘以\(10^3\)）和均匀采样点的交并比(gIoU)进行评估。TurboSquid具有更有趣的表面特征，因此我们使用基于3D几何的度量以及基于32个多视图渲染图像的图像空间度量。具体来说，我们计算分割掩码的交并比(iIoU)和使用掩码交集上的L2距离的图像空间法线对齐。形状复杂度大致在数据集上增加。我们为ShapeNet150和Thingi32训练5个LOD，为TurboSquid训练6个LOD。对于数据集准备，我们遵循DualSDF[16]，对网格进行归一化，移除内部三角形，并使用光线穿刺[35]对距离进行符号化。

存储(KB)对应于解码器大小和表示的总和，假设32位精度。对于我们的架构，解码器参数占用90 KB的存储空间，因此对于较低的LOD，有效存储大小更小，因为解码器能够泛化到多个形状。推理参数数量是距离查询所需的参数数量，这与推理所需的浮点运算数量大致相关。

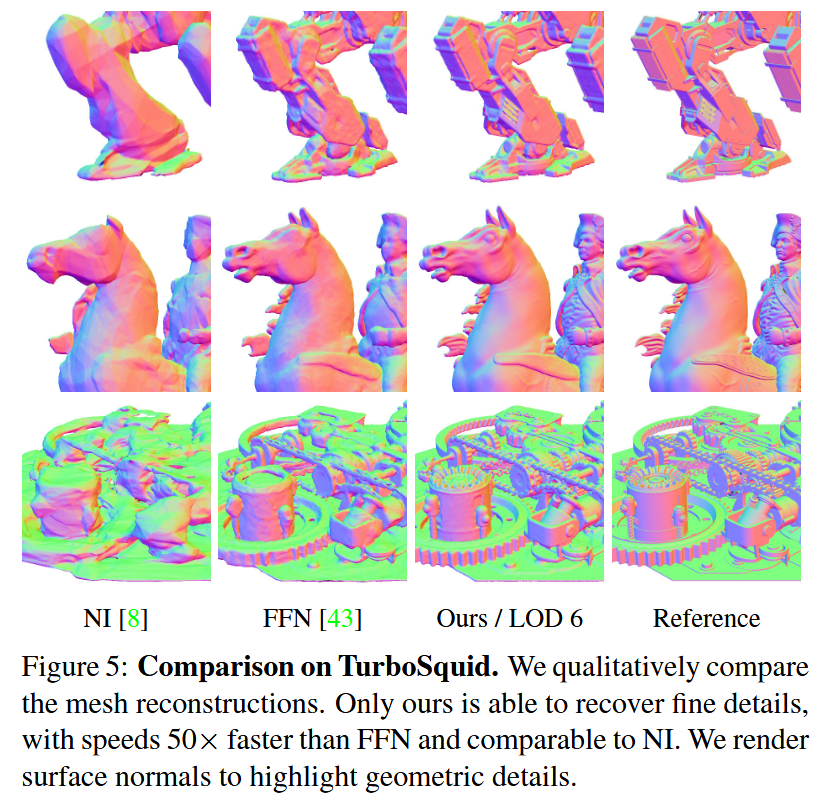
nglod.fig.5

图5：在TurboSquid上的比较。我们对网格重建进行了定性比较。只有我们的方法能够恢复精细细节，速度比FFN快50倍，与NI相当。我们渲染表面法线以突出几何细节。

在所有数据集和度量标准上，我们都达到了最先进的结果。值得注意的是，我们的表示从第三个LOD开始显示更好的结果，此时我们的存储影响最小。我们还注意到，我们的推理成本在所有分辨率上固定为4,737个浮点数，与FFN[43]相比需要少99%的推理参数，与神经隐式[8]相比少37%，同时显示更好的重建质量（见图5的定性评估）。

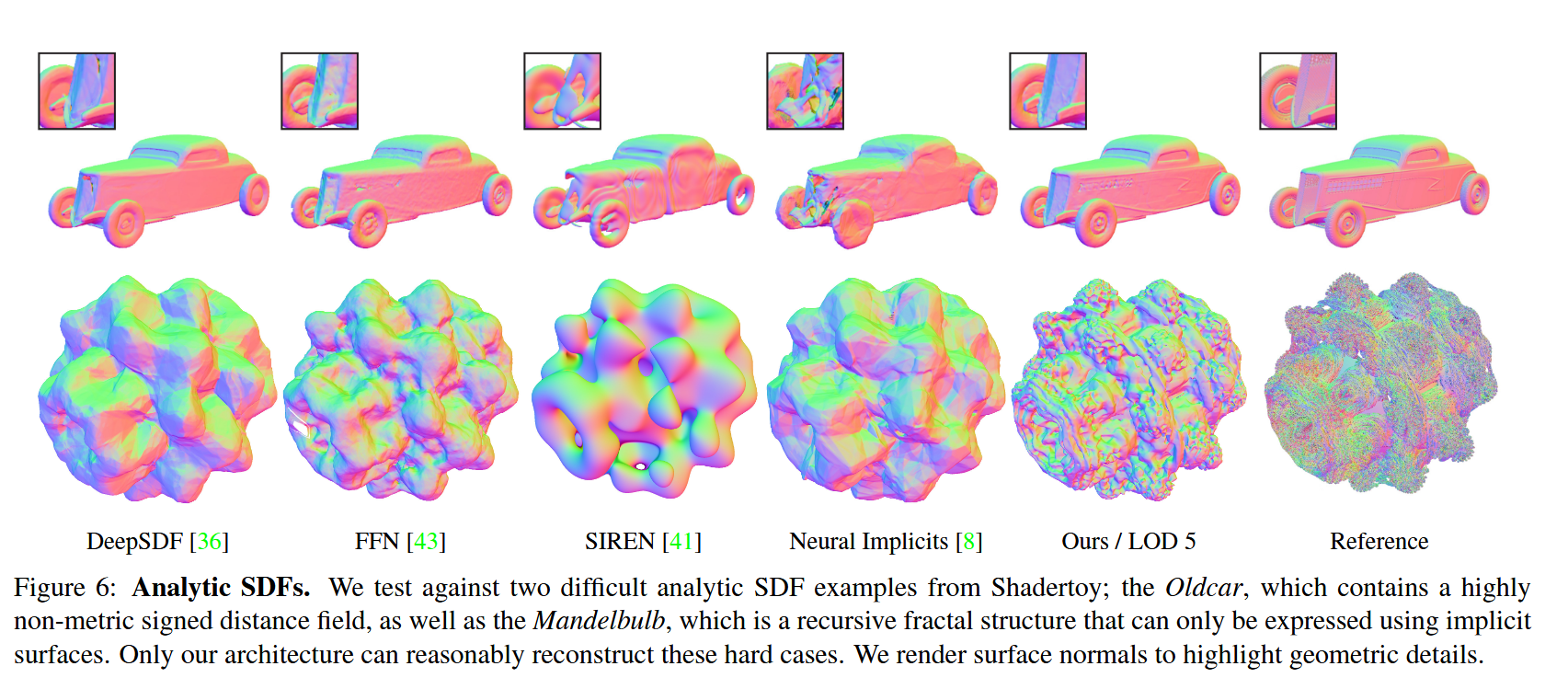
nglod.fig.6

图6：解析SDF。我们针对来自Shadertoy的两个具有挑战性的解析SDF示例进行了测试：Oldcar，它包含高度非度量的有向距离场；以及Mandelbulb，这是一种递归分形结构，只能使用隐式表面来表达。只有我们的架构能够合理地重建这些困难的案例。我们渲染表面法线以突出几何细节。

特殊情况解析SDF。我们还评估了从Shadertoy收集的两个特别困难的解析SDF的重建。Oldcar模型是一个高度非度量SDF，它不满足Eikonal方程\(\vert\nabla f\vert = 1\)并包含不连续性。这是一个需要处理的关键情况，因为非度量SDF经常被用于特殊效果和更容易的SDF建模。Mandelbulb是一个具有无限分辨率的递归分形。这两个SDF都由数学表达式定义，我们从中提取并采样距离值。我们对这些解析形状训练100个周期，每个周期有\(5 \times 10^6\)个样本。只有我们的架构能够以合理的精度捕捉这些复杂例子的高频细节。值得注意的是，FFN[43]和SIREN[41]似乎完全失败；这可能是因为它们只能拟合平滑的距离场，无法处理不连续性和递归结构。见图6的定性比较。

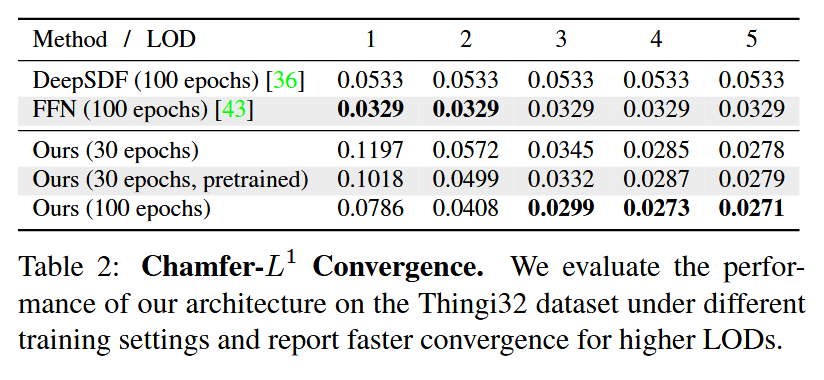
nglod.table.2

表2： Chamfer-\(L^1\)收敛性。我们在不同训练设置下，在Thingi32数据集上评估我们架构的性能，并报告更高LOD下更快的收敛速度。

收敛性。我们进行实验评估我们架构的训练收敛速度。表2显示了Thingi32上我们的模型完全训练100个周期、训练30个周期以及从斯坦福Lucy雕像（图1）的预训练权重训练30个周期的重建结果。我们发现我们的架构收敛迅速，即使只有DeepSDF[36]和FFN[43]训练时间的约45%（它们训练了完整的100个周期），也能实现更好的重建。从预训练权重微调有助于较低的LOD，但差异很小。我们的表示能迅速收敛到良好的解决方案。

4.2 渲染性能

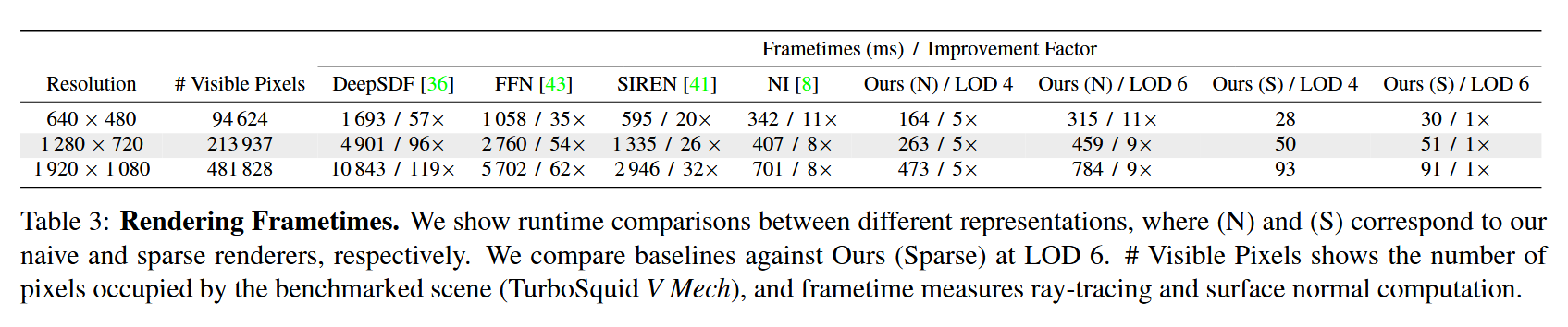
nglod.table.3

表3：渲染帧时间。我们展示了不同表示方法之间的运行时比较，其中(N)和(S)分别对应我们的简单渲染器和稀疏渲染器。我们将基线与我们在LOD 6时的稀疏渲染器（Ours (Sparse)）进行比较。“可见像素数量（# Visible Pixels）”表示基准场景（TurboSquid V Mech）所占据的像素数量，帧时间衡量光线追踪和表面法线计算。

我们还评估了我们架构的推理性能，包括使用和不使用我们的渲染算法的情况。我们首先使用PyTorch[37]中的朴素Python球体追踪算法进行性能评估，为了公平比较，所有基准模型使用相同的实现。对于我们表示的Python版本，我们将特征存储在密集体素网格上，因为朴素的球体追踪器无法处理稀疏性。对于优化实现，我们展示了使用libtorch[37]、CUB[30]和CUDA实现的渲染器的表示性能。表3显示了TurboSquid V Mech场景在各种不同分辨率下的帧时间。在这里，我们将帧时间测量为球体追踪和法线计算的CUDA时间。#可见像素列显示了模型在图像中占据的像素数量。我们看到，我们的朴素PyTorch渲染器和稀疏优化CUDA渲染器的性能都优于基准模型。特别是，稀疏帧时间比DeepSDF快100多倍，同时以更少的参数实现更好的视觉质量。我们还注意到，随着LOD的降低，我们朴素渲染器的帧时间显著减少，但优化渲染器的减少程度较小。这是因为渲染的瓶颈不在于光线-八叉树相交（这取决于体素数量），而是在MLP推理和杂项内存I/O。我们相信通过缓存小型MLP解码器来最小化数据移动，仍有显著的改进空间。尽管如此，较低的LOD仍然受益于较低的内存消耗和存储。

4.3 泛化

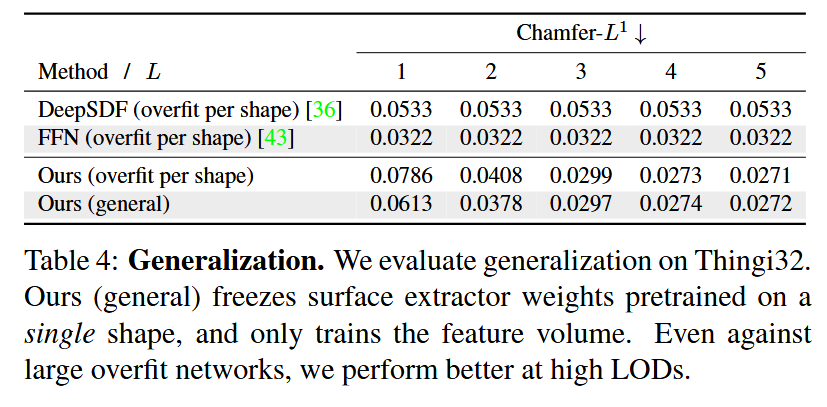
nglod.table.4

表4：泛化能力。我们在Thingi32上评估泛化能力。我们的通用方法（Ours (general)）冻结在单个形状上预训练的表面提取器权重，仅训练特征体。即使与大型过拟合网络相比，我们在高LOD下的表现也更好。

我们现在展示我们的表面提取机制可以泛化到多个形状，即使只从单个形状训练。这很重要，因为像[8, 41]那样为每个对象加载不同的权重会产生大量的内存移动，这是昂贵的。通过通用的表面提取机制，权重可以预先加载，多分辨率体素可以按需流入。表4显示了Thingi32的结果。DeepSDF[36]、FFN[43]和我们的（过拟合）模型都是针对每个形状过拟合的。我们的（通用）模型首先在斯坦福Lucy模型上过拟合架构，固定表面提取网络权重，然后只训练稀疏特征。我们看到我们的表示表现更好，即使与针对每个特定形状示例过拟合的大型网络相比也是如此。在最低LOD，表面提取器难以重建良好的表面，这是预期的；对于较低的LOD，特征变得越来越高级和复杂。

4.4 几何简化

nglod.fig.7

图7：与网格简化的比较。在低内存预算下，从较低的法向\(L^2\)误差可以看出，我们的模型比网格简化更能保持视觉细节。

在这最后一个实验中，我们评估我们的低LOD与经典网格抽取算法的表现对比，特别是libigl[19]中的边缘折叠[14]。我们与网格抽取而非网格压缩算法[1]进行比较，因为我们的模型也可以从压缩中受益，而网格解码会产生额外的运行时成本。我们首先评估我们的内存影响，即\(M = (m + 1) \vert V_{1:L_{max}}\vert\)字节，其中\(m + 1\)是特征维度以及用于索引的Z顺序曲线[33]，\(\vert V_{1:L_{max}}\vert\)是八叉树大小。然后我们计算面预算为\(F = M/3\)，因为连接性可以是任意的。因此，我们选择一个保守的预算来有利于网格表示。图7显示了Thingi32中狮子雕像的结果。我们看到，随着内存预算的减少，我们方法在感知质量上的相对优势增加，这从基于图像的法线误差可以看出。SDF可以轻松表示平滑特征，而随着面预算的减少，网格会遭受离散化误差。我们的表示还可以通过构造在LOD之间平滑混合，这对于网格来说很难做到。

5 局限性和未来工作

总结来说，我们引入了神经几何LOD，这是一种隐式3D形状的表示方法，它实现了最先进的几何重建质量，同时允许在可接受的内存占用下进行实时渲染。我们的模型结合了一个小型表面提取神经网络和一个稀疏八叉树数据结构，该结构编码几何并自然地启用LOD。结合定制的球体追踪算法，这导致了一种既具有计算性能又高度表现力的方法。

我们的方法严重依赖于训练期间使用的点样本。因此，将我们的表示扩展到极大的场景或非常薄的、无体积的几何是困难的。此外，我们无法使用传统方法轻松地为我们的几何添加动画或变形。我们将这些挑战确定为未来研究的有前途方向。尽管如此，我们相信我们的模型代表了基于神经隐式函数几何的重大进步，据我们所知，这是第一个可以实时渲染和查询的此类表示。我们希望它将成为许多下游应用的重要组成部分，如场景重建、超精确机器人路径规划、交互式内容创建等。

致谢。我们感谢Jean-Francois Lafleche、Peter Shirley、Kevin Xie、Jonathan Granskog、Alex Evans和Alex Bie在整个项目中的有趣讨论。我们还感谢Jacob Munkberg、Peter Shirley、Alexander Majercik、David Luebke、Jonah Philion和Jun Gao帮助审阅论文。

评论