论文重点和难点

1 论文的核心观点

• 深度学习并非与众不同：作者认为深度神经网络（DNNs）的某些现象（如过参数化、良性过拟合、双下降等）并非深度学习所独有，也不应被视为神秘或需要重新思考泛化理论的现象。这些现象可以通过现有的泛化框架（如PAC-Bayes和可数假设界限）来解释。

• 软归纳偏差（Soft Inductive Biases）：作者提出“软归纳偏差”是理解这些现象的关键。与传统的限制性归纳偏差（通过限制假设空间来避免过拟合）不同，软归纳偏差允许模型在灵活的假设空间中偏好某些解，而不是完全排除其他解。这种偏好可以通过正则化、贝叶斯先验或架构设计实现。

2 主要现象的解释

• 良性过拟合（Benign Overfitting）：模型能够完美拟合噪声数据，但仍能在结构化数据上泛化得很好。这种现象可以通过软归纳偏差解释：模型在拟合数据时偏好简单解，即使在噪声数据上也能保持这种偏好。PAC-Bayes和可数假设界限可以为这种现象提供严格的泛化保证。

• 双下降（Double Descent）：随着模型参数数量的增加，泛化误差先下降、再上升、最后再次下降。这种现象可以通过有效维度（Effective Dimensionality）和软归纳偏差解释：当模型参数过多时，平坦解（即简单解）在假设空间中的占比增加，从而改善泛化性能。

• 过参数化（Overparametrization）：模型参数数量远大于数据点数量，但仍然能够泛化。作者指出，参数数量本身并不是模型复杂度的准确衡量，而是模型的压缩能力和偏好简单解的能力决定了泛化性能。

3 泛化框架的对比

• PAC-Bayes和可数假设界限：这些框架关注模型的先验偏好，而不是假设空间的大小。它们可以为过参数化模型提供非空泛化界限，并且对大型模型的泛化能力提供有力解释。

• 其他框架（如Rademacher复杂度、VC维度）：这些框架主要关注假设空间的大小，对过参数化模型的泛化能力无法提供有效解释。例如，Rademacher复杂度会因为模型能够拟合噪声而变得无效。

4 深度学习的独特性

尽管作者认为深度学习的某些现象并非独有，但论文也指出深度学习在其他方面具有独特性：

• 表示学习（Representation Learning）：深度神经网络能够学习数据的层次化表示，这种表示学习能力使其在高维自然信号（如图像、文本）上表现出色。

• 模式连通性（Mode Connectivity）：深度神经网络的解空间中存在简单的路径，连接不同的局部最优解，这些路径上的解能够保持接近零的训练损失。这一现象表明深度学习模型的解空间具有独特的结构。

• 通用性（Universality）：大型语言模型（LLMs）等深度学习模型表现出对多种任务和模态的通用性，例如在未经过特定任务训练的情况下，仍能进行零样本学习。

5 难点与挑战

• 软归纳偏差的实现：如何在实际模型中设计和实现有效的软归纳偏差是一个挑战。例如，如何通过架构设计或正则化方法来引导模型偏好简单解，同时保持足够的灵活性以适应复杂数据。

• 泛化框架的适用性：虽然PAC-Bayes和可数假设界限能够解释许多现象，但如何将这些理论框架应用于更复杂的模型（如大型语言模型）仍然是一个研究热点。

• 优化器的作用：尽管论文指出优化器的隐式偏差并非深度学习泛化的必要条件，但优化器在实际训练中的作用仍然需要进一步研究，尤其是在计算资源受限的情况下如何设计更有效的优化器。

6 实验与验证

• 论文中通过多个实验验证了软归纳偏差和泛化框架的有效性。例如：

• 使用高阶多项式模型和高斯过程（Gaussian Process, GP）复现了深度学习中的良性过拟合和双下降现象。

• 通过调整模型参数数量和数据复杂度，展示了软归纳偏差在不同数据规模和复杂度下的适应性。

• 使用ResNet和线性模型展示了双下降现象，并通过有效维度解释了其背后的机制。

7 总结

论文的核心在于强调深度学习的泛化行为可以通过现有的理论框架解释，而无需重新发明轮子。同时，论文也指出了深度学习在表示学习、模式连通性和通用性等方面的独特性，这些特性是深度学习区别于其他模型类的关键。

论文详细讲解

1. 引言

论文的核心观点是深度学习并非神秘或与众不同，其表现出的“异常”泛化行为（如过参数化、良性过拟合和双下降）可以通过现有的泛化理论（如PAC-Bayes和可数假设界限）来解释。作者强调，理解深度学习不需要重新思考泛化理论，而是需要重新审视和应用已有的理论框架。

2. 软归纳偏差（Soft Inductive Biases）

软归纳偏差是论文的核心概念之一，它允许模型在灵活的假设空间中偏好某些解，而不是完全排除其他解。与传统的限制性归纳偏差不同，软归纳偏差通过正则化或贝叶斯先验实现，能够引导模型选择更简单、更压缩的解。

例如，对于高阶多项式模型，通过引入顺序依赖的正则化项（如 $\sum_{j} \gamma^j w_j^2$），模型在拟合数据时会优先选择低阶项，只有在必要时才会使用高阶项。这种偏好机制使得模型即使在高维空间中也能保持良好的泛化能力。

3. 泛化框架

论文对比了几种不同的泛化框架，重点讨论了PAC-Bayes和可数假设界限。

• PAC-Bayes框架：通过考虑模型参数的分布，PAC-Bayes能够为过参数化模型提供非空的泛化界限。它关注模型的先验偏好，而不是假设空间的大小。例如，对于一个具有大量参数的模型，PAC-Bayes可以通过衡量模型的压缩能力来评估其泛化性能：

\[R(h) \leq \hat{R}(h) + \frac{\text{KL}(Q \| P) + \log(n/\delta)}{2n}\]

其中，$R(h)$ 是期望风险，$\hat{R}(h)$ 是经验风险，$\text{KL}(Q | P)$ 是模型后验分布与先验分布的KL散度。

• 可数假设界限：该框架通过衡量模型的压缩能力和先验概率来评估泛化性能。它适用于确定性模型，并且可以为大型模型提供非空的泛化界限：

\[R(h) \leq \hat{R}(h) + \frac{\log(1/P(h)) + \log(1/\delta)}{2n}\]

其中，$P(h)$ 是模型的先验概率。

这些框架能够解释深度学习中的许多现象，如过参数化和良性过拟合，而传统的Rademacher复杂度和VC维度则无法提供有效的解释。

4. 良性过拟合（Benign Overfitting）

良性过拟合是指模型能够完美拟合噪声数据，但在结构化数据上仍然能够泛化得很好。论文通过简单的多项式模型和高斯过程（GP）复现了这一现象，并通过PAC-Bayes和可数假设界限提供了理论解释。

例如，对于一个高阶多项式模型，通过引入顺序依赖的正则化项，模型在拟合噪声数据时会偏好简单解（低阶项），从而避免过拟合。这种偏好机制可以通过PAC-Bayes框架进行量化：

\[R(h) \leq \hat{R}(h) + \frac{K(h) \log 2 + \log(1/\delta)}{2n}\]

其中，$K(h)$ 是模型的Kolmogorov复杂度，衡量模型的压缩能力。

5. 过参数化（Overparametrization）

过参数化是指模型的参数数量远大于数据点数量，但仍然能够泛化。论文指出，过参数化模型的泛化能力可以通过其压缩能力和偏好简单解的能力来解释。

例如，高斯过程（GP）可以被视为一种过参数化模型，它通过无限数量的基函数来拟合数据，但仍然能够通过偏好简单解（如低秩解）来实现良好的泛化性能。论文通过实验表明，随着模型参数数量的增加，模型的有效维度（Effective Dimensionality）会降低，从而提高泛化能力。

6. 双下降（Double Descent）

双下降是指随着模型参数数量的增加，泛化误差先下降、再上升、最后再次下降的现象。论文通过实验和理论分析解释了这一现象。

例如，对于一个线性模型，当参数数量 $d$ 小于数据点数量 $n$ 时，模型的泛化误差会随着 $d$ 的增加而降低；当 $d > n$ 时，模型开始过拟合，泛化误差上升；随着 $d$ 继续增加，模型的有效维度降低，泛化误差再次下降。这一现象可以通过PAC-Bayes和可数假设界限进行解释：

\[R(h) \leq \hat{R}(h) + \frac{\log(1/P(h)) + \log(1/\delta)}{2n}\]

其中，$P(h)$ 与模型的压缩能力相关。

7. 深度学习的独特性

尽管论文指出深度学习的某些现象并非独有，但深度学习在其他方面具有独特性：

• 表示学习（Representation Learning）：深度神经网络能够学习数据的层次化表示，这种表示学习能力使其在高维自然信号（如图像、文本）上表现出色。例如，卷积神经网络（CNN）通过学习图像的局部特征来实现更好的泛化性能。

• 模式连通性（Mode Connectivity）：深度神经网络的解空间中存在简单的路径，连接不同的局部最优解，这些路径上的解能够保持接近零的训练损失。这一现象表明深度学习模型的解空间具有独特的结构。

• 通用性（Universality）：大型语言模型（LLMs）等深度学习模型表现出对多种任务和模态的通用性，例如在未经过特定任务训练的情况下，仍能进行零样本学习。

8. 实验验证

论文通过多个实验验证了其理论观点：

• 多项式模型：使用高阶多项式模型复现了良性过拟合现象，展示了顺序依赖的正则化如何引导模型偏好简单解。

• 高斯过程（GP）：通过GP复现了深度学习中的良性过拟合和双下降现象，展示了GP在过参数化情况下的泛化能力。

• ResNet和线性模型：通过ResNet和线性模型展示了双下降现象，并通过有效维度解释了其背后的机制。

9. 结论

论文的核心结论是，深度学习的泛化行为可以通过现有的理论框架（如PAC-Bayes和可数假设界限）来解释，而无需重新发明轮子。同时，论文也指出了深度学习在表示学习、模式连通性和通用性等方面的独特性，这些特性是深度学习区别于其他模型类的关键。

论文具体内容解析

结构化数据和非结构化数据

1. Benign Overfitting Benign overfitting describes the ability for a model to fit noise with no loss, but still generalize well on structured data. It shows that a model can be capable of overfitting data, but won’t tend to overfit structured data. The paper understanding deep learning requires re-thinking generalization (Zhang et al., 2016) drew significant attention to this phenomenon by showing that convolutional neural networks could fit images with random labels, but generalize well on structured image recognition problems such as CIFAR. The result was presented as contradicting what we know about generalization, based on frameworks such as VC dimension and Rademacher complexity, and distinct to neural networks. The authors conclude with the claim: “We argue that we have yet to discover a precise formal measure under which these enormous models are simple.” Five years later, the authors maintain the same position, with an extended paper entitled understanding deep learning (still) requires re-thinking generalization (Zhang et al., 2021). Similarly, Bartlett et al. (2020) note “the phenomenon of benign overfitting is one of the key mysteries uncovered by deep learning methodology: deep neural networks seem to predict well, even with a perfect fit to noisy training data.”

在机器学习和深度学习的上下文中，”结构化数据”和”非结构化数据”通常指的是数据的组织形式和复杂性：

1. 结构化数据（Structured Data）

结构化数据是指具有明确组织格式的数据，通常以表格形式呈现，例如数据库中的行和列。这类数据通常具有清晰的模式和规则，易于被算法处理。例如：

• 图像识别任务中的图像数据（如CIFAR数据集），尽管图像本身是像素矩阵，但其内容通常具有明确的语义结构（如物体类别）。

• 表格数据、时间序列数据等。

在本文中，”结构化数据”指的是那些具有内在规律或模式的数据，例如图像识别任务中的图像，这些数据通常可以通过模型学习到有效的特征，从而实现良好的泛化。

2. 非结构化数据（Unstructured Data）

非结构化数据是指没有固定格式或明确组织的数据，通常难以用传统的表格或规则表示。例如：

• 纯噪声数据（如随机生成的标签或像素值）。

• 文本、音频、视频等。

在本文中，”非结构化数据”指的是那些没有内在规律或模式的数据，例如随机生成的标签或噪声。模型可以完美拟合这些数据，但由于缺乏内在结构，这种拟合通常不会带来良好的泛化性能。

在上下文中的具体含义

• “Generalize well on structured data”：模型能够在具有内在规律或模式的数据（如图像识别任务中的图像）上表现出良好的泛化性能。

• “Fit noise with no loss”：模型能够完美拟合没有内在规律或模式的数据（如随机生成的标签或噪声），但这种拟合通常不会带来泛化能力的提升。

例子

• CIFAR数据集：这是一个结构化数据集，因为其图像内容具有明确的语义类别（如飞机、汽车等），模型可以通过学习这些结构化的特征来实现良好的泛化。

• 随机标签：这是一种非结构化数据，因为标签是随机生成的，没有内在规律，模型可以完美拟合这些标签，但这种拟合不会带来泛化能力的提升。

总结来说，结构化数据具有内在的规律或模式，而非结构化数据则缺乏这种规律。模型在结构化数据上通常能够实现良好的泛化，而在非结构化数据上则可能表现出过拟合但无法泛化的现象。

原文翻译

深度学习并非如此神秘或与众不同

Andrew Gordon Wilson

纽约大学

摘要

深度神经网络通常被视为与其他模型类别不同，因为它们违背了传统的泛化观念。常见的异常泛化行为包括良性过拟合、双下降和过参数化的成功。我们认为，这些现象并非神经网络所独有，也并非特别神秘。此外，这些泛化行为可以通过直觉理解，并使用长期存在的泛化框架（如PAC-Bayes和可数假设界）进行严格刻画。我们提出软归纳偏差作为解释这些现象的关键统一原则：与其通过限制假设空间来避免过拟合，不如采用灵活的假设空间，并对与数据一致的简单解给予软偏好。这一原则可以编码到许多模型类别中，因此深度学习并不像它看起来那样神秘或与其他模型类别不同。然而，我们也强调深度学习在其他方面的相对独特性，例如其表示学习能力、模式连通性等现象，以及其相对普遍性。

1 引言

“教科书必须重写！”

深度神经网络通常被认为是神秘且与其他模型类别不同的，其行为可能违背传统的泛化观念。当被问及深度学习有何不同时，人们通常会提到过参数化、双下降和良性过拟合等现象（Zhang et al., 2021; Nakkiran et al., 2020; Belkin et al., 2019; Shazeer et al., 2017）。我们的观点是，这些现象并非神经网络所独有，也并非特别神秘。此外，虽然一些泛化框架如VC维度（Vapnik, 1998）和Rademacher复杂度（Bartlett & Mendelson, 2002）无法解释这些现象，但它们可以通过其他长期存在的框架如PAC-Bayes（McAllester, 1999; Catoni, 2007; Dziugaite & Roy, 2017）甚至简单的可数假设泛化界（Valiant, 1984; Shalev-Shwartz & Ben-David, 2014; Lotfi et al., 2024a）进行正式描述。换句话说，理解深度学习并不需要重新思考泛化，也从未需要。

我们并不旨在论证深度学习已被完全理解，也不打算全面综述理解深度学习现象的工作，或为解释某些现象的历史优先权分配。我们也不声称是第一个注意到这些现象可以通过其他模型类别重现的人。事实上，我们想明确指出，在理解深度学习中被视为神秘的泛化行为方面，已经取得了显著进展，并且与普遍看法相反，这些行为大多适用于深度学习之外，并可以使用存在了几十年的框架进行正式解释。如果教科书几十年前就关注了已知的泛化知识，它们就不需要重写！相反，我们需要搭建桥梁，并承认进展。

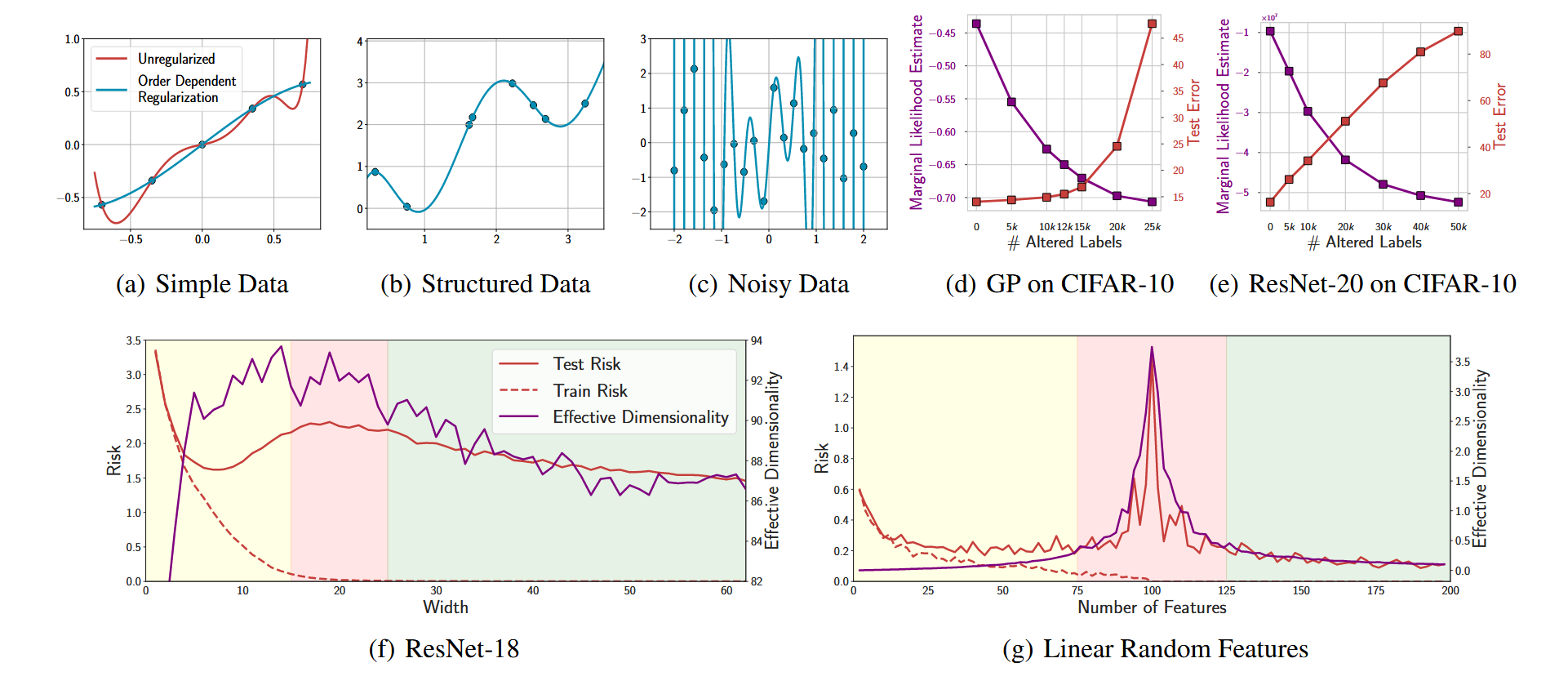
图1. 深度学习中出现的泛化现象可以通过简单的线性模型重现并得到理解。上图：良性过拟合。一个带有阶数相关正则化的150阶多项式能够合理地描述(a)简单和(b)复杂结构的数据，同时也能完美拟合(c)纯噪声。(d) 高斯过程完美重现了Zhang等人(2016)在CIFAR-10上的结果，完美拟合了噪声标签，但仍然实现了合理的泛化。此外，对于高斯过程和(e) ResNet，边际似然（直接对应于PAC-Bayes边界[Germain等人，2016]）随着标签被篡改的程度增加而降低，如Wilson & Izmailov (2020)所述。下图：双下降现象。(f) ResNet和(g)线性随机特征模型都表现出双下降现象，在低训练损失区域，有效维度紧密跟踪第二次下降，如Maddox等人(2020)所述。

确实，我们将通过尽可能简单的例子（通常是基本的线性模型）来重现这些现象并解释其背后的直觉。希望通过依赖特别简单的例子，我们能够强调这些泛化行为并非神经网络所独有，并且可以通过基本原理来理解。例如，在图1中，我们展示了良性过拟合和双下降可以通过简单的线性模型重现和解释。

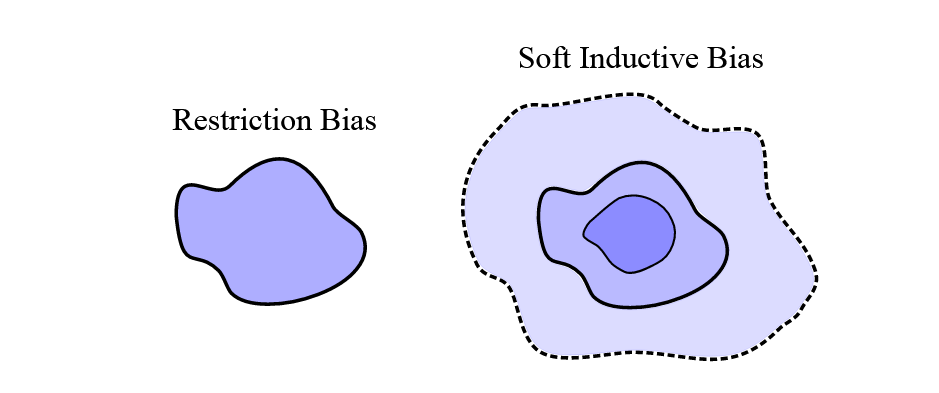
图3. 软归纳偏差使得假设空间灵活而不会过拟合。许多泛化现象可以通过软归纳偏差的概念来理解：与其限制模型可以表示的解决方案，不如指定对某些解决方案的偏好。在这种概念化中，我们通过用浅蓝色表示偏好较低的假设来扩大假设空间，而不是完全限制它们。实现软归纳偏差的方法有很多。与其使用低阶多项式，不如使用带有阶数相关正则化的高阶多项式。或者，与其限制模型具有平移等变性（例如ConvNet），不如通过压缩偏差（例如transformer或带有ConvNet偏差的RPP）来表示对不变性的偏好。过参数化是另一种实现软偏差的方式。

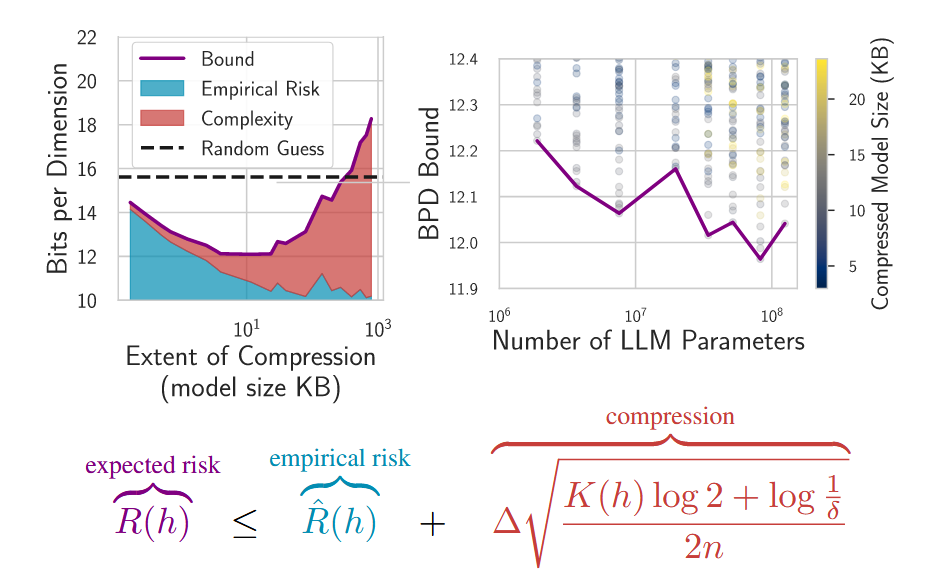
图2. 泛化现象可以通过泛化边界进行形式化描述。泛化可以通过假设$h$的经验风险和可压缩性进行上界估计，如第3.1节所述。可压缩性以Kolmogorov复杂度$K(h)$形式化，可以进一步通过模型的文件大小进行上界估计。大模型能够很好地拟合数据，并且可以有效地压缩为较小的文件大小。与Rademacher复杂度不同，这些边界不会因为假设空间$H$能够拟合噪声而惩罚模型，并且描述了良性过拟合、双下降和过参数化现象。它们甚至可以为LLMs提供非空边界，如Lotfi等人(2024a)所述。

我们还将通过软归纳偏差的统一概念来共同处理这些现象。虽然归纳偏差通常被认为是限制偏差——通过限制假设空间的大小来提高数据效率和泛化能力——但实际上并不需要限制偏差。相反，我们可以采用任意灵活的假设空间，并结合软偏差，表达对某些解决方案的偏好，而不完全排除任何解决方案，如图3所示。PAC-Bayes等框架完全符合这种归纳偏差的观点，能够为具有数十亿参数的模型生成非空泛化界，只要这些模型对某些解决方案有先验偏好（Lotfi et al., 2024b）。广义而言，一个大的假设空间，结合对简单解决方案的偏好，提供了一个可证明有效的性能提升方法，如图2所示。

还有一些最近引起关注的现象，如缩放定律和“顿悟”（grokking），但这些并非我们的重点，因为它们通常不被视为与泛化理论不一致，或为神经网络所独有。然而，我们注意到第3节中的PAC-Bayes和可数假设泛化框架也与LLM（大型语言模型）一致，甚至与Chinchilla缩放定律一致（Hoffmann et al., 2022; Finzi et al., 2025）。此外，深度学习当然在其他方面是不同且神秘的。在第8节中，我们讨论了深度神经网络的相对独特特征，如表示学习、模式连通性和广泛成功的上下文学习。

我们从第2节对软归纳偏差的讨论开始，这为全文提供了统一的直觉。然后在第3节简要介绍几个通用框架和定义，通过这些预备知识，我们将在接下来的章节中探讨泛化现象。在全文，我们特别对比了第3.1节中的PAC-Bayes和可数假设框架（这些框架确实刻画了这些泛化现象）与第3.3节中的Rademacher复杂度和VC维度等其他泛化框架（这些框架无法刻画这些现象）。接着，我们在第4、5、6节分别讨论了良性过拟合、过参数化和双下降，第7节提出了替代观点，第8节讨论了独特特征和开放问题。

2 软归纳偏差

我们通常认为归纳偏差是限制偏差：对假设空间的约束，使其与感兴趣的问题对齐。换句话说，有许多参数设置可能拟合数据但泛化能力较差，因此我们将假设空间限制为更可能为所考虑问题提供良好泛化的参数设置。此外，由于假设空间较小，它会更快地被数据约束，因为我们有更少的解决方案需要在新数据点加入时“排除”。卷积神经网络提供了一个经典例子：我们从多层感知器（MLP）开始，移除参数并强制参数共享，从而为局部性和平移等变性提供硬约束。

但限制偏差不仅不必要，甚至可能是不理想的。我们希望支持任何能够描述数据的解决方案，这意味着采用灵活的假设空间。例如，我们可能怀疑数据仅近似平移等变。我们可以偏向模型使其倾向于平移等变性，而无需任何硬约束。一种提供软卷积网络偏差的简单方法是：从MLP开始，然后引入一个正则化项，惩罚任何在卷积网络中不存在的参数的范数，以及任何在卷积网络中共享的参数之间的距离。我们可以通过正则化强度来控制这种偏差。残差路径先验提供了一种更实用和通用的机制，将硬架构约束转化为软归纳偏差（Finzi et al., 2021）。

图3. 软归纳偏差使得假设空间灵活而不会过拟合。许多泛化现象可以通过软归纳偏差的概念来理解：与其限制模型可以表示的解决方案，不如指定对某些解决方案的偏好。在这种概念化中，我们通过用浅蓝色表示偏好较低的假设来扩大假设空间，而不是完全限制它们。实现软归纳偏差的方法有很多。与其使用低阶多项式，不如使用带有阶数相关正则化的高阶多项式。或者，与其限制模型具有平移等变性（例如ConvNet），不如通过压缩偏差（例如transformer或带有ConvNet偏差的RPP）来表示对不变性的偏好。过参数化是另一种实现软偏差的方式。

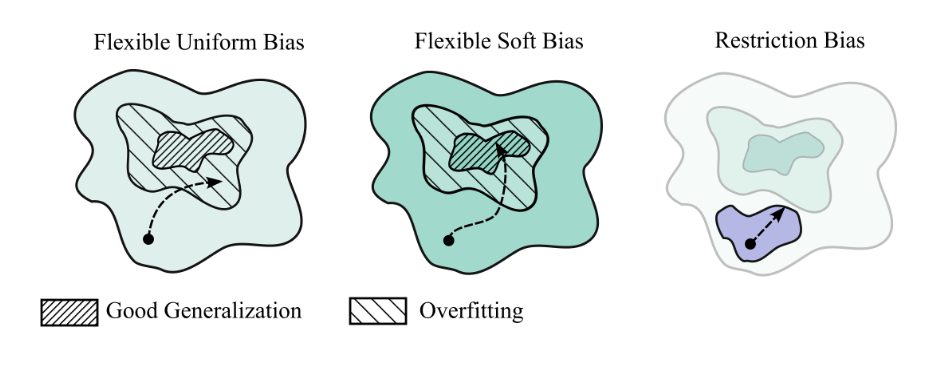
图4. 通过软归纳偏差实现良好的泛化。左图：一个大的假设空间，但对拟合数据相同的解决方案没有偏好。因此，训练通常会导致泛化性能较差的过拟合解决方案。中图：软归纳偏差通过表示灵活的假设空间并结合对不同解决方案的偏好（用不同深浅表示）来引导训练实现良好的泛化。右图：限制假设空间可以通过仅考虑具有某些理想属性的解决方案来帮助防止过拟合。然而，通过限制表达能力，模型无法捕捉现实的细微差别，从而阻碍了泛化。

我们将对某些解决方案的偏好这一总体概念称为软归纳偏差，即使它们对数据的拟合程度相同。我们将软偏差与更标准的限制偏差进行对比，后者对假设空间施加硬约束。我们在图3中展示了软归纳偏差的概念，并在图4中展示了软归纳偏差如何影响训练过程。正则化以及模型参数的贝叶斯先验为创建软归纳偏差提供了机制。然而，正则化通常不用于放松架构约束，正如我们将看到的，软偏差更为通用，并且可以由架构本身诱导。

作为一个运行示例，考虑一个高阶多项式，但我们对其高阶系数的正则化强度大于低阶系数。换句话说，我们用$f(x, w) = \sum_{j=0}^J w_j x^j$拟合数据，并对$w_j$施加一个随$j$增加的正则化项。最后，我们有一个数据拟合项，由涉及$f(x, w)$的似然$p(y\vert f(x, w))$形成。因此，我们的总损失为：

\[\text{Loss} = \text{data fit} + \text{order dependent complexity penalty}\]

例如，可以表示为$L(w) = -\log p(y\vert f(x, w)) + \sum_j \gamma_j w_j^2$，其中$\gamma > 1$。对于分类，观测模型$p(y_i\vert f(x_i, w)) = \text{softmax}(f(x_i, w))$将导致交叉熵损失$-\log p(y\vert f(x, w))$。对于回归，$p(y_i\vert f(x_i, w)) = \mathcal{N}(f(x_i, w), \sigma^2)$将导致平方误差数据拟合项，除以$1/(2\sigma^2)$。

图1. 深度学习中出现的泛化现象可以通过简单的线性模型重现并得到理解。上图：良性过拟合。一个带有阶数相关正则化的150阶多项式能够合理地描述(a)简单和(b)复杂结构的数据，同时也能完美拟合(c)纯噪声。(d) 高斯过程完美重现了Zhang等人(2016)在CIFAR-10上的结果，完美拟合了噪声标签，但仍然实现了合理的泛化。此外，对于高斯过程和(e) ResNet，边际似然（直接对应于PAC-Bayes边界[Germain等人，2016]）随着标签被篡改的程度增加而降低，如Wilson & Izmailov (2020)所述。下图：双下降现象。(f) ResNet和(g)线性随机特征模型都表现出双下降现象，在低训练损失区域，有效维度紧密跟踪第二次下降，如Maddox等人(2020)所述。

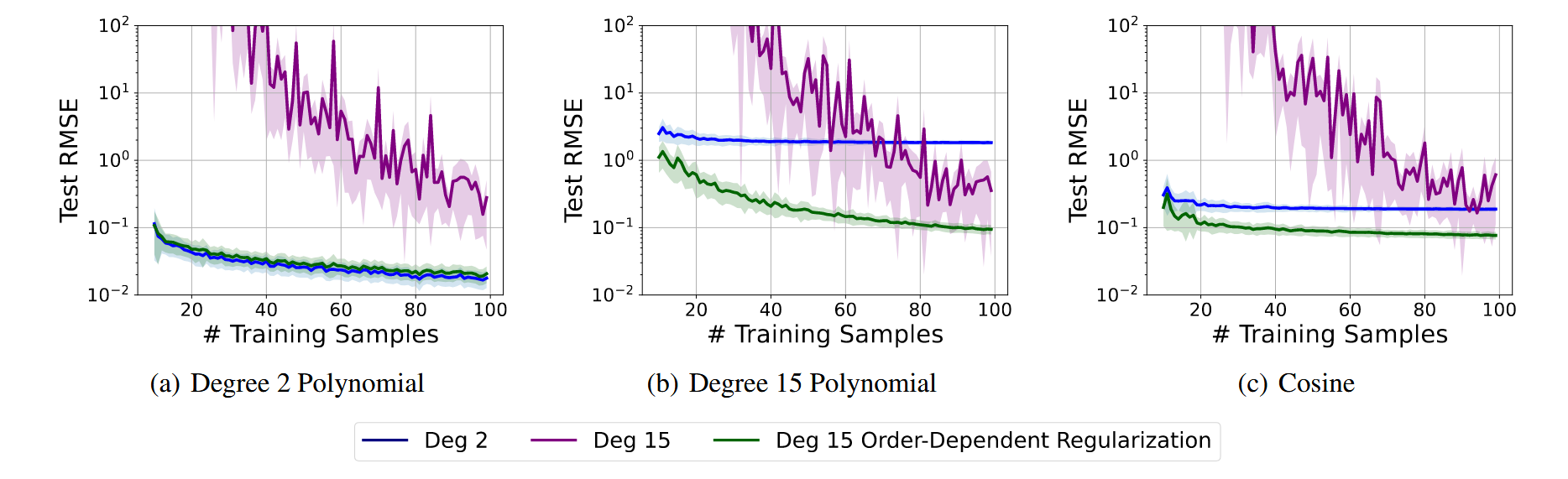
图5. 具有简单性偏差的灵活性适用于不同数据规模和复杂度的问题。我们使用2阶、15阶和正则化的15阶多项式来拟合由(a)-(c)描述的函数生成的三个不同训练数据规模的回归问题。我们使用一种特殊的正则化惩罚，该惩罚随着多项式系数的阶数增加而增加。我们展示了100次拟合的100个测试样本的平均性能±1个标准差。通过仅在需要时增加复杂度以拟合数据，正则化的15阶多项式在所有数据规模和不同复杂度问题上都优于或与其他模型相当。

如果我们将多项式的阶数$J$设得很大，那么我们有一个灵活的模型。但模型具有简单性偏差：由于阶数相关的复杂性惩罚，它将尽可能使用低阶项拟合数据，只有在必要时才使用高阶项。例如，想象一个简单的一维回归问题，数据落在一条直线上。对于大$J$，有许多系数${w_j}$的设置可以完美拟合数据。但模型会偏好简单的直线拟合，即$w_j = 0$（$j \geq 2$），因为它与数据一致且惩罚最低，如图1（左上）所示。实际上，我们放松了低阶多项式的硬限制偏差，并将其转化为软归纳偏差。这种模型对于任何规模的训练集都有效：在小数据集上，它与具有硬约束的模型竞争；在大数据集上，它与相对无约束的模型竞争，如图5所示。

虽然$l_2$和$l_1$（或Lasso）正则化是标准实践，但它并不用于构建任意大小模型的处方。阶数相关正则化的思想较少为人所知。Rasmussen & Ghahramani (2000) 表明，贝叶斯边际似然（证据），即从先验生成训练数据的概率，倾向于具有类似阶数相关参数先验的高阶傅里叶模型。参数先验$p(w)$诱导函数先验$p(f(x, w))$，从贝叶斯角度来看，正是这个函数先验控制模型的泛化性质（Wilson & Izmailov, 2020）。阶数相关的先验会生成一个可能生成数据的函数先验，即使是高阶模型。另一方面，在Rasmussen & Ghahramani (2000) 的六年后，经典教科书Bishop (2006) 在第3章第168页中认为，边际似然与传统模型选择观念一致，正是因为它选择了一个中间阶数的多项式，而不是小或大的多项式。实际上，这一教科书结果只是不良先验的产物：它使用了各向同性参数先验（类似于$l_2$正则化），而具有各向同性参数先验的高阶多项式不太可能生成数据。如果Bishop (2006) 选择了阶数相关的先验，边际似然可能偏好任意高阶模型。

在残差路径先验（RPP）（Finzi et al., 2021）中，研究表明，对于给定问题，对等变性约束的软偏差通常与完美约束的模型一样有效。例如，对旋转等变性的软偏差对于分子（旋转不变）的效果与旋转等变模型一样好。在仅接触少量数据后，软偏差会收敛到近乎完美的旋转等变性，因为模型被鼓励（但不受约束）用对称性表示数据，即使数据量很小，它也能做到这一点。此外，在数据仅包含近似对称性或根本没有对称性的情况下，RPP方法显著优于具有硬对称性约束的模型。

令人惊讶的是，训练后的视觉Transformer甚至比卷积神经网络更具平移等变性（Gruver et al., 2023）！这一发现可能看起来不可能，因为卷积神经网络在架构上被约束为平移等变。然而，在实践中，等变性被混叠伪影破坏。等变性对称性提供了一种压缩数据的机制，正如我们将在后续章节中讨论的，Transformer对压缩具有软归纳偏差。

我们认为，软归纳偏差，而不是限制假设空间，是构建智能系统的关键处方。

3 泛化框架

到目前为止，我们一直在论证，我们直观上希望采用一个灵活的假设空间，因为它代表了我们关于现实世界数据具有复杂结构的真实信念。但为了获得良好的泛化能力，我们必须对某些类型的解决方案具有先验偏好，即使我们允许任何类型的解决方案存在。虽然我们讨论的泛化现象违背了一些关于过拟合和泛化观念（如Rademacher复杂度）的传统智慧（Zhang et al., 2016; 2021），但它们完全符合这一直觉。

事实证明，这些现象也可以通过存在了几十年的泛化框架进行正式刻画，包括PAC-Bayes（McAllester, 1999; Guedj, 2019; Alquier et al., 2024）和简单的可数假设界（Valiant, 1984; Shalev-Shwartz & Ben-David, 2014）。我们将在第3.1节介绍这些框架。然后在第3.2节定义有效维度，我们将在后文回到这一概念以提供直觉。最后，我们在第3.3节介绍无法描述这些现象的框架，但它们极大地影响了关于泛化的传统思维。

本节简要介绍一些定义和泛化框架——这些预备知识将用于我们在后续章节中探讨泛化现象。

3.1 PAC-Bayes与可数假设界

PAC-Bayes和可数假设界为大型甚至过参数化模型提供了一种引人注目的方法，因为它们关注的是哪些假设是可能的，而不仅仅是假设空间的大小（Catoni, 2007; Shalev-Shwartz & Ben-David, 2014; Dziugaite & Roy, 2017; Arora et al., 2018b; P ́erez-Ortiz et al., 2021; Lotfi et al., 2022a）。它们与第2节中软归纳偏差的概念相协调，后者提供了一种机制，通过结合任意大的假设空间和对某些解决方案的偏好（独立于它们对数据的拟合程度）来实现良好的泛化。

定理3.1（可数假设界）

考虑有界风险$R(h, x) \in [a, a + \Delta]$，以及一个可数假设空间$h \in \mathcal{H}$，对此我们有一个先验$P(h)$。设经验风险$\hat{R}(h) = \frac{1}{n} \sum_{i = 1}^{n} R(h, x_i)$是对于固定假设$h$，独立随机变量$R(h, x_i)$的和。设$R(h) = \mathbb{E}[\hat{R}(h)]$为期望风险。

那么，至少以$1 - \delta$的概率有：

\[R(h) \leq \hat{R}(h) + \Delta\sqrt{\frac{\log \frac{1}{P(h)} + \log \frac{1}{\delta}}{2n}} \tag{1}\]

这个界与有限假设界相关，但包含了一个先验$P(h)$，并且假设空间是可数的而非有限的（[Shalev - Shwartz & Ben - David, 2014]第7.3章）。我们可以将先验看作一个加权函数，它对某些假设的权重高于其他假设。重要的是，我们可以使用任何先验来评估这个界：它不需要生成数据的真实假设，甚至不需要被训练用于寻找某个假设$h^*$的模型所使用。如果模型使用的先验与用于评估公式(1)的先验有很大不同，那么这个界就会变得宽松。我们在附录C中包含了这个界的一个基本证明。

我们可以通过所罗门诺夫先验$P(h) \leq 2^{-K(h\vert A)}$（[Solomonoff, 1964]）推导出有信息的界，其中$K$是将模型架构$A$作为输入时，$h$的无前缀柯尔莫哥洛夫复杂度。将这个先验代入公式(1)中：

\[\overbrace{R(h)}^{\text{期望风险}} \leq \overbrace{\hat{R}(h)}^{\text{经验风险}} + \overbrace{\Delta\sqrt{\frac{K(h\vert A) \log 2 + \log \frac{1}{\delta}}{2n}}}^{\text{压缩}} \tag{2}\]

假设$h$的无前缀柯尔莫哥洛夫复杂度$K(h)$，是对于固定编程语言生成$h$的最短程序的长度（[Kolmogorov, 1963]）。虽然我们无法计算最短程序，但我们可以通过处理$K(h\vert A)$，将架构以及任何不由数据决定的常数纳入先验中。然后我们可以从无前缀柯尔莫哥洛夫复杂度转换为标准柯尔莫哥洛夫复杂度，以计算上界：

\[\begin{align} \log 1/P(h) &\leq K(h\vert A) \log 2 \tag{3}\\ &\leq C(h) \log 2 + 2 \log C(h) \tag{4} \end{align}\]

其中$C(h)$是使用某些预先指定的编码表示假设$h$所需的比特数。因此，即使是具有许多参数的大型模型，只要它们表示的假设具有低经验风险和小的压缩大小，就能够实现强大的泛化保证。

PAC - 贝叶斯界（PAC - Bayes bounds）可以通过考虑期望解的分布$Q$，进一步将从$\log_2 \frac{1}{P(h)}$所需的比特数降低为$\mathbb{KL}(Q | P)$ 。如果我们对采样的$Q$的具体元素不关心，那么我们可以回收这些比特，用于编码不同的消息。

由于具有点质量后验$Q$的PAC - 贝叶斯界可以恢复类似于公式(1)的界（[Lotfi 等人, 2022b]），我们有时会将这两个界都称为PAC - 贝叶斯界。我们还注意到，边缘似然（即从模型先验生成训练数据的概率）直接对应于一个PAC - 贝叶斯界（[Germain 等人, 2016]；[Lotfi 等人, 2022b]）。

这些泛化框架已经被调整，以便为具有数百万甚至数十亿参数的模型提供有意义的泛化保证。它们适用于经过确定性训练的模型，并且也已被调整应用于大语言模型（LLMs），以适应无界的每维度比特数（每令牌纳特数）损失、随机训练以及令牌之间的依赖性（[Lotfi 等人, 2023]；[2024b]；[Finzi 等人, 2025]）。此外，计算这些界很直接。例如：(i) 使用任何优化器训练一个模型以找到假设$h^{\star}$；(ii) 测量经验风险$\hat{R}(h^{\star})$（例如，训练损失）；(iii) 测量存储模型的文件大小以得到$C(h^{\star})$；(iv) 将公式(4)代入公式(2)。

换句话说，我们可以将这些泛化界解释为：

\[\text{期望风险} \leq \text{经验风险} + \text{模型可压缩性}\]

图2. 泛化现象可以通过泛化边界进行形式化描述。泛化可以通过假设$h$的经验风险和可压缩性进行上界估计，如第3.1节所述。可压缩性以Kolmogorov复杂度$K(h)$形式化，可以进一步通过模型的文件大小进行上界估计。大模型能够很好地拟合数据，并且可以有效地压缩为较小的文件大小。与Rademacher复杂度不同，这些边界不会因为假设空间$H$能够拟合噪声而惩罚模型，并且描述了良性过拟合、双下降和过参数化现象。它们甚至可以为LLMs提供非空边界，如Lotfi等人(2024a)所述。

其中可压缩性为复杂性提供了一种形式化描述。在图2中（改编自[Lotfi 等人 (2023)]），我们可视化了每个项对该界的贡献。这种界的表示也为构建通用学习器提供了一种方法：将灵活的假设空间与对低柯尔莫哥洛夫复杂度的偏好相结合。

一个灵活的模型将能够在各种数据集上实现低经验风险（训练损失）。能够压缩这些模型可以证明会带来良好的泛化性能。[Goldblum 等人 (2024)] 表明，神经网络，尤其是大型变换器，倾向于偏好低柯尔莫哥洛夫复杂度，现实世界数据的分布也是如此。因此，单个模型可以在许多现实世界问题上实现良好的泛化。

事实上，即使在一个由所有可能程序组成的最大灵活假设空间中，如果我们选择一个对数据拟合良好且复杂度低的假设，那么根据可数假设界（式(1)），我们就能保证泛化能力。我们可以将这一洞见与Solomonoff归纳联系起来，它提供了一种最大过参数化的过程，对假设的复杂度或参数数量没有限制，但形式化了一个理想的学习系统（Solomonoff, 1964; Hutter, 2000）。通过对更简单（更短）的程序分配指数级更高的权重，Solomonoff归纳确保了即使假设空间非常庞大，所选择的假设在拟合数据良好的情况下也会是简单的。

一般来说，关于PAC-Bayes和可数假设界存在一些常见的误解。例如，它们不仅适用于参数分布，也适用于具有确定性参数的模型。此外，随着模型规模的增大，最近的界变得更紧，而不是更松。我们在附录A中讨论了一些误解。值得注意的是，这些界不仅对大型神经网络是非空泛的，而且可以出奇地紧。例如，Lotfi et al. (2022a) 在CIFAR10数据集上，以至少95%的概率将具有数百万参数的模型的分类误差上界定为16.6%，这在该基准上表现相当不错。

3.2 有效维度

有效维度为解释泛化现象提供了有用的直觉。矩阵$A$的有效维度定义为$N_{\text{eff}}(A) = \sum_i \frac{\lambda_i}{\lambda_i + \alpha}$，其中$\lambda_i$是$A$的特征值，$\alpha$是正则化参数。有效维度衡量了相对较大特征值的数量。损失函数Hessian矩阵的有效维度（在参数$w$处评估）衡量了损失景观中“尖锐”方向的数量——即由数据确定的参数数量。

有效维度较低的解更平坦，意味着相关参数可以在不显著增加损失的情况下被扰动。平坦性并不是影响泛化的唯一因素，且通过Hessian矩阵衡量的平坦性并不是参数化不变的（如SGD、$l_2$正则化和许多标准过程），这意味着很容易找到或构建平坦解并不泛化得更好的例子（例如，Dinh et al., 2017）。另一方面，平坦性与泛化之间的联系并非虚假的经验关联。我们对平坦性如何导致更好的泛化有机制性理解：平坦解更具可压缩性，具有更好的奥卡姆因子，往往导致更宽的决策边界和更紧的泛化界（Hinton & Van Camp, 1993; Hochreiter & Schmidhuber, 1997; MacKay, 2003; Keskar et al., 2016; Izmailov et al., 2018; Foret et al., 2020; Maddox et al., 2020）。

与Rademacher复杂度类似，有效维度本身并不是泛化界，但它是一个直观的量，可以正式纳入泛化界（MacKay, 2003; Dziugaite & Roy, 2017; Maddox et al., 2020; Jiang et al., 2019）。它还与其他在解释泛化现象中经常出现的概念密切相关，例如模型的有效秩（Bartlett et al., 2020）和“松散模型”（Quinn et al., 2022）。

在讨论泛化现象时，我们经常会回到有效维度以提供直觉。

3.3 其他泛化框架

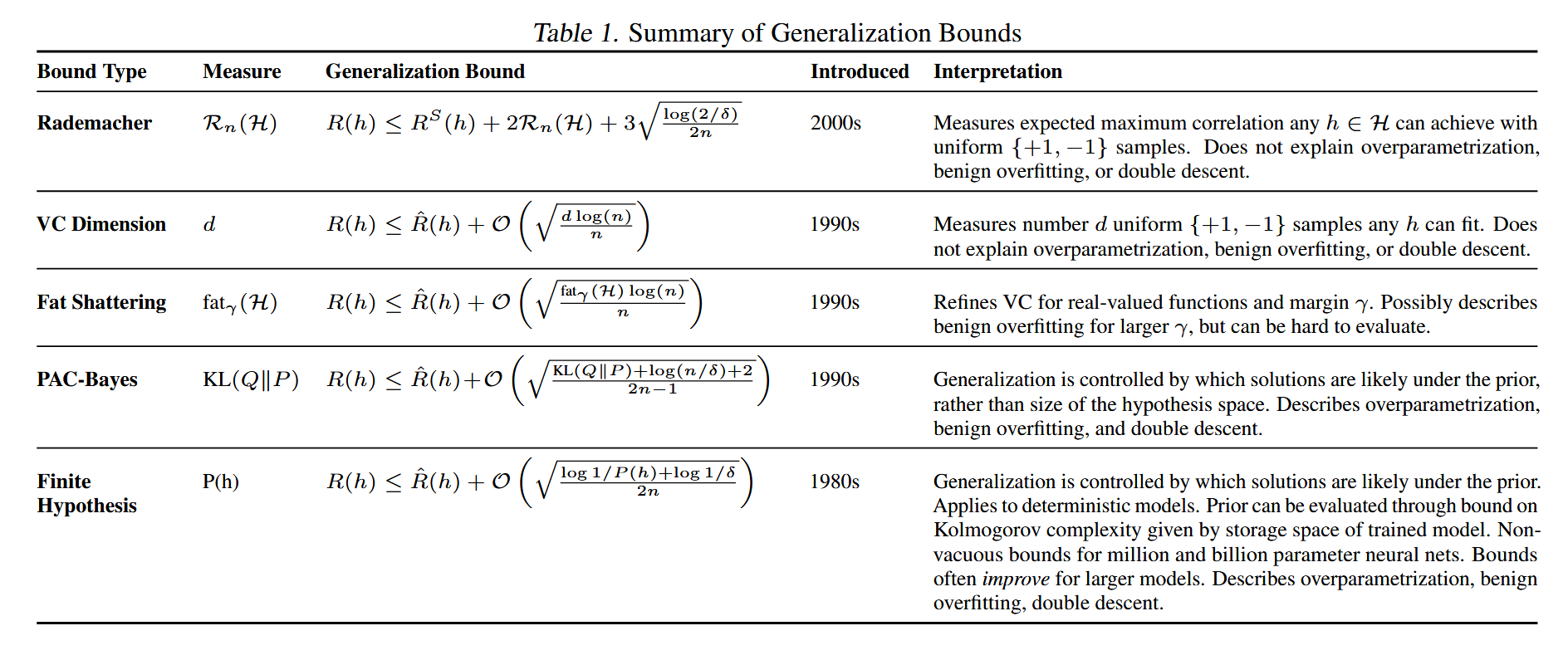
表1. 泛化边界总结

Rademacher复杂度（Bartlett & Mendelson, 2002）精确衡量了模型拟合均匀${+1, -1}$随机噪声的能力。类似地，VC维度（Vapnik et al., 1994）衡量了假设空间$H$可以“粉碎”任何$d$个带${+1, -1}$标签的点的最大整数$d$。脂肪粉碎维度（Alon et al., 1997）$\text{fat}_\gamma(H)$通过某种边距$\gamma$对VC维度进行了细化，以衡量“粉碎”标签的能力。与PAC-Bayes不同，所有这些框架都惩罚整个假设空间$H$的大小，提出了限制偏差的处方，而不是第2节中的软归纳偏差。我们在附录B中进一步讨论了这些框架，并在表1中进行了比较总结。

4 良性过拟合

良性过拟合描述了模型能够完美拟合噪声但仍能在结构化数据上良好泛化的能力。它表明模型可能过拟合数据，但不会倾向于过拟合结构化数据。论文《理解深度学习需要重新思考泛化》（Zhang et al., 2016）通过展示卷积神经网络可以拟合随机标签的图像，但在结构化图像识别问题（如CIFAR）上表现良好，引起了广泛关注。这一结果被认为与基于VC维度和Rademacher复杂度等框架的泛化知识相矛盾，并且是神经网络所特有的。作者总结道：“我们认为，我们尚未发现一个精确的正式度量，能够证明这些庞大模型是简单的。”五年后，作者在扩展论文《理解深度学习（仍然）需要重新思考泛化》（Zhang et al., 2021）中保持了相同的立场。同样，Bartlett et al. (2020) 指出：“良性过拟合现象是深度学习方法揭示的关键谜团之一：深度神经网络似乎在完美拟合噪声训练数据的情况下仍能做出良好的预测。”

然而，良性过拟合行为可以通过其他模型类别重现，可以直观理解，并且可以通过存在了几十年的严谨泛化框架进行描述。

图1. 深度学习中出现的泛化现象可以通过简单的线性模型重现并得到理解。上图：良性过拟合。一个带有阶数相关正则化的150阶多项式能够合理地描述(a)简单和(b)复杂结构的数据，同时也能完美拟合(c)纯噪声。(d) 高斯过程完美重现了Zhang等人(2016)在CIFAR-10上的结果，完美拟合了噪声标签，但仍然实现了合理的泛化。此外，对于高斯过程和(e) ResNet，边际似然（直接对应于PAC-Bayes边界[Germain等人，2016]）随着标签被篡改的程度增加而降低，如Wilson & Izmailov (2020)所述。下图：双下降现象。(f) ResNet和(g)线性随机特征模型都表现出双下降现象，在低训练损失区域，有效维度紧密跟踪第二次下降，如Maddox等人(2020)所述。

直觉。直观上，要重现良性过拟合，我们只需要一个灵活的假设空间，结合一个要求拟合数据的损失函数，以及一个简单性偏好：在符合数据的解（即完美拟合数据）中，更简单的解更受青睐。以回归为例，考虑第2节中具有阶数相关正则化的简单多项式模型。在我们的似然中，我们将$\sigma$设为一个较小的值，因此模型将优先拟合数据（平方误差乘以一个大数）。然而，模型强烈倾向于使用低阶项，因为系数的范数随阶数增加而受到更强的惩罚。简单的结构化数据将通过简单、结构化且可压缩的函数拟合，从而泛化，但模型会根据需要调整其复杂度以拟合数据，包括纯噪声，如图1（顶部）所示。换句话说，如果理解深度学习需要重新思考泛化，那么理解这个简单多项式也需要，因为这个多项式展现了良性过拟合！

正式泛化框架。良性过拟合也可以通过PAC-Bayes和可数假设界进行刻画，这些是刻画泛化的正式且长期存在的框架。我们可以为表现出良性过拟合的神经网络评估这些界，提供非空泛化保证（Dziugaite & Roy, 2017; Zhou et al., 2018; Lotfi et al., 2022a）。此外，如第3节所述，这些泛化框架可以通过Kolmogorov复杂度精确定义大型神经网络的简单性。事实上，更大的神经网络通常对低Kolmogorov复杂度解有更强的偏好（Goldblum et al., 2024）。

图1. 深度学习中出现的泛化现象可以通过简单的线性模型重现并得到理解。上图：良性过拟合。一个带有阶数相关正则化的150阶多项式能够合理地描述(a)简单和(b)复杂结构的数据，同时也能完美拟合(c)纯噪声。(d) 高斯过程完美重现了Zhang等人(2016)在CIFAR-10上的结果，完美拟合了噪声标签，但仍然实现了合理的泛化。此外，对于高斯过程和(e) ResNet，边际似然（直接对应于PAC-Bayes边界[Germain等人，2016]）随着标签被篡改的程度增加而降低，如Wilson & Izmailov (2020)所述。下图：双下降现象。(f) ResNet和(g)线性随机特征模型都表现出双下降现象，在低训练损失区域，有效维度紧密跟踪第二次下降，如Maddox等人(2020)所述。

信号与噪声的混合。拟合信号与噪声混合但仍能实现良好泛化的能力也可以通过第3.1节中的泛化框架重现和刻画。特别是，我们可以完全重现Zhang et al. (2021) 中CIFAR-10的混合噪声标签实验，如图1(d)(e)所示，遵循Wilson & Izmailov (2020)。这里，高斯过程（GP）被拟合到CIFAR-10上，训练误差为零，但增加了越来越多的错误标签。泛化能力是合理的，并随着错误标签的增加而逐渐下降。重要的是，GP和ResNet的边际似然都下降，而边际似然直接与PAC-Bayes泛化界对齐（Germain et al., 2016）。

良性过拟合的研究。目前已有大量研究通过其他模型类别研究和重现良性过拟合。然而，良性过拟合作为一种神秘且深度学习特有的现象、一种仍需重新思考泛化的观念仍然存在。我们无意也不可能在这里涵盖所有这些工作，但我们注意到一些关键进展。Dziugaite & Roy (2017) 展示了在结构化和噪声MNIST上训练的神经网络的非空和空PAC-Bayes界。Smith & Le (2018) 展示了在MNIST上逻辑回归的良性过拟合，并使用贝叶斯奥卡姆因子（MacKay, 2003）解释结果。多项研究分析了两层网络（例如，Cao et al., 2022; Kou et al., 2023）。Wilson & Izmailov (2020) 使用高斯过程和贝叶斯神经网络完全重现了Zhang et al. (2016) 的实验，并通过边际似然解释结果。Bartlett et al. (2020) 展示了线性回归模型可以重现良性过拟合。他们通过研究数据协方差矩阵的秩和最小范数最小二乘解来理解这一现象，这与Maddox et al. (2020) 通过有效维度解释双下降的方式相关。我们将在接下来的过参数化和双下降章节中回到这一推理。

结论。《理解深度学习（仍然）需要重新思考泛化》（Zhang et al., 2021）提出了测试：“对于任何声称的泛化度量，我们现在可以比较它在自然数据和随机数据上的表现。如果它在两种情况下相同，它不可能是一个好的泛化度量，因为它甚至无法区分从自然数据（可以泛化）学习和从随机数据（无法泛化）学习。”PAC-Bayes和可数假设界显然通过了这一测试，并且提供了“一个精确的正式度量，证明这些庞大模型是简单的”，而Rademacher复杂度和VC维度则无法做到。此外，从软归纳偏差的角度来看，这种泛化行为是直观可理解的，即采用灵活的假设空间并结合压缩偏好。

5 过参数化（Overparametrization）

现在我们已经讨论了软归纳偏差和良性过拟合，模型拥有许多参数并不必然导致过拟合数据这一观点可能正变得越来越直观。一般来说，参数计数是衡量模型复杂度的糟糕代理。实际上，在深度学习于2012年复兴之前，使用大量参数的模型已经成为一种常见做法：“贝叶斯学者现在通常会拟合参数数量多于数据点数量的模型……” [MacKay, 1995]。我们感兴趣的不是孤立的参数，而是参数如何控制我们用来拟合数据的函数的性质。我们已经看到，只要存在简单性偏好，任意高阶的多项式也不会过拟合数据。高斯过程（Gaussian Processes, GP）也提供了令人信服的例子。具有径向基函数（RBF）核的GP可以由无限多个密集分布的径向基函数的和推导而来：$f(x, w) = \sum_{i=1}^{\infty} w_i \varphi_i(x)$ [MacKay, 1998]。同样，利用中心极限定理的论证，我们可以推导出对应于无限单层和多层神经网络的GP核 [Neal, 1996b; Lee et al., 2017]（其中第一个结果曾被NeurIPS拒绝！）。实际上，GP通常比任何标准神经网络都更灵活，但由于其强大的（但软的）简单性偏好，它们在小数据集上相对于其他模型类往往表现得更好。

5.1 过参数化的成功是否令人惊讶？

对于过参数化是否真的令人惊讶，似乎并没有达成共识。一方面，在某些圈子里，人们已经知道并且理解具有任意多参数的模型可以泛化；事实上，追求大模型的极限一直是非参数方法几十年来的指导原则（例如，[MacKay, 1995; Neal, 1996a; Rasmussen, 2000; Rasmussen & Ghahramani, 2000; Beal et al., 2001; Rasmussen & Ghahramani, 2002; Griffiths & Ghahramani, 2005; Williams & Rasmussen, 2006]）。与此同时，过参数化一直是神经网络的一个显著特征。许多论文，尤其是理论论文，都以对深度神经网络能够泛化表示惊讶为开头，尽管它们的参数数量多于数据点，尤其是在良性过拟合的背景下：例如，“深度网络的一个谜团是，尽管参数数量远多于训练样本数量，它们仍然能够泛化……” [Arora et al., 2018a]。此外，随着参数数量的增加，许多泛化界限也变得越来越宽松，最终变得毫无意义 [Jiang et al., 2019]。

然而，最近也有一些泛化界限随着参数数量的增加而变得更加紧密 [Lotfi et al., 2022a; 2024b]。尽管在许多情况下大型语言模型（LLMs）并不算过参数化，但参数计数比以往任何时候都更为普遍。双下降（double descent，见第6节）的展示通常也基于参数计数。

5.2 为什么增加参数数量可以提升性能？

有两个原因：灵活性和压缩性。我们已经讨论过，具有高灵活性和压缩偏好的模型可以提供良好的泛化保证（见第3节）。在神经网络中增加参数数量直接提升了其灵活性。或许更令人惊讶的是，增加参数数量也会增加压缩偏好：也就是说，经过训练后，参数更多的模型可以比参数更少的模型用更少的总内存进行存储。

Maddox等人（2020）通过测量Hessian的有效维度（见第3.2节），发现经过训练的大型模型比小型模型具有更少的有效参数。在更近期的研究中，Goldblum等人（2024）也表明，大型语言模型具有更强的简单性偏好——它们生成的序列具有更低的Kolmogorov复杂度——这种偏好是跨多种不同设置和模态实现良好性能和良好上下文学习的重要特征。

但为什么更大的模型似乎具有更强的压缩偏好呢？尽管这是一个引人入胜的开放性问题，但已经有一些线索和直觉。Bartlett等人（2020）表明，过参数化的最小二乘模型越来越倾向于低有效秩的小范数解（更多内容见第6节）[Bartlett et al., 2020]。随着参数数量的增加，我们还可以在损失景观中指数级地增加平坦解的体积，使这些解更容易被找到（Huang等人，2019）[Huang et al., 2019]，这得到了大型模型具有更小有效维度的实证支持（Maddox等人，2020）[Maddox et al., 2020]。这也帮助解释了为什么随机优化的隐式偏好，与普遍观点相反，并非深度学习泛化所必需的：尽管某些参数设置会过拟合数据，但这些设置在数量上远远少于那些既能拟合数据又能泛化的参数设置。实际上，Geiping等人（2021）发现，对于大型残差网络的训练，全批量梯度下降几乎可以和随机梯度下降（SGD）表现得一样好[Geiping et al., 2021]，而Chiang等人（2022）进一步表明，即使是“猜测与检查”——随机采样参数向量并在找到低损失解时停止——也可以与随机训练提供具有竞争力的泛化性能[Chiang et al., 2022]。

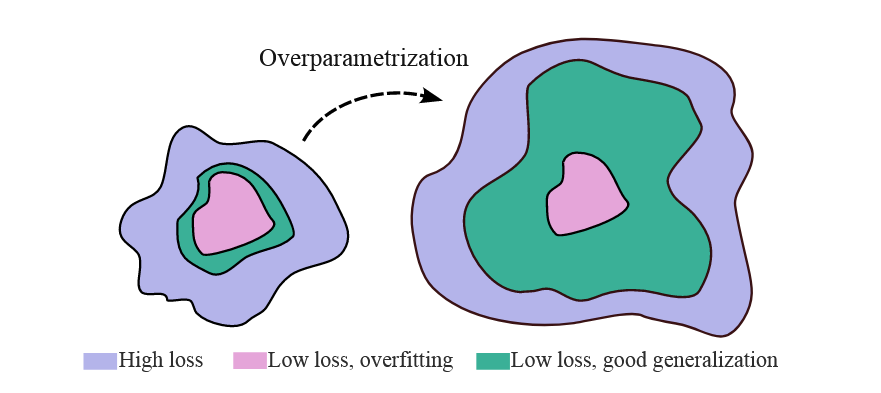
图6. 增加参数可以改善泛化。通过增加参数数量，平坦的解决方案（通常提供更简单且可压缩的数据解释）在总假设空间中占据更大的相对体积——这导致了对这些简单解决方案的隐式软归纳偏差。尽管过参数化模型通常表示许多过拟合数据的假设（例如参数设置），但它们可以表示更多拟合数据良好并提供良好泛化的假设。过参数化可以同时增加假设空间的大小和对简单解决方案的偏差。

通常人们认为灵活性与归纳偏差之间存在一种张力，假设更灵活的模型必然具有更弱的归纳偏差。但正如我们所见，不仅灵活性与归纳偏差之间不一定存在权衡，而且更大、更灵活的模型往往具有更强的归纳偏差，我们在图6中对此进行了说明。

6 双下降

双下降通常指泛化误差（或损失）随着模型参数数量的增加而先减小、再增大、然后再次减小的现象。训练损失通常在第二次下降开始时接近零。第一次下降和随后的上升对应于“经典区域”，模型最初捕捉到更多有用的数据结构，改善了泛化，但随后开始过拟合数据。第二次下降（因此得名“双下降”）被称为“现代插值区域”。

双下降由Belkin et al. (2019) 引入现代机器学习社区，并在Nakkiran et al. (2020) 中针对深度神经网络进行了深入研究。它通常被认为是深度学习的重大谜团之一，第二次下降挑战了关于泛化的传统智慧。如果增加模型灵活性在经典区域导致过拟合，那么进一步增加灵活性如何能缓解过拟合？Belkin et al. (2019) 甚至推测了双下降“历史缺失”的原因。

但双下降并非现代深度学习现象。双下降的最早引入至少可以追溯到三十年前的Opper et al. (1989)，并在Opper et al. (1990)、LeCun et al. (1991) 和B ̈os et al. (1993) 中也有提及。它也可以通过其他模型类别理解和重现。事实上，Belkin et al. (2019) 的论文本身除了展示两层全连接神经网络的双下降外，还展示了随机森林和随机特征模型的双下降。

双下降也可以被理解。随着参数数量的增加，最初拟合数据的能力提高，学习到的参数具有更高的有效维度（第3.2节）。一旦参数数量增加到我们可以在所有完美拟合数据的参数设置之间进行选择时，损失值不再是选择参数的唯一决定因素。随着我们继续增加参数数量，平坦解的数量增加，使得这些解在训练过程中更容易被发现。因此，解的有效维度会降低，泛化能力会提高。

这一解释适用于线性模型和神经网络，但我们可以通过线性模型获得更多洞见。假设我们有$Xw = y$，其中$X$是$n \times d$的特征矩阵，$w$表示$d$个参数，$y$是$n$个数据点。一旦$d > n$，模型可以通过无限多个参数设置$w$完美插值数据。随着$d$继续增加，未确定的参数数量以及损失中的平坦方向增加。最小二乘解为$w^* = (X^\top X)^{-1}X^\top y$。对于$d > n$，Hessian矩阵$X^\top X$最多有$n$个非零特征值。随着$d$继续增加，信号将分布在更多参数上，导致单个参数的确定性降低，有效维度减小。或者，$w^*$提供了最小$l_2$范数解，偏向于主要依赖特征空间中最具信息量的方向的简单模型（Bartlett et al., 2020）。与良性过拟合一样，这些简单性概念可以通过可数假设或PAC-Bayes界进行正式刻画。

图1. 深度学习中出现的泛化现象可以通过简单的线性模型重现并得到理解。上图：良性过拟合。一个带有阶数相关正则化的150阶多项式能够合理地描述(a)简单和(b)复杂结构的数据，同时也能完美拟合(c)纯噪声。(d) 高斯过程完美重现了Zhang等人(2016)在CIFAR-10上的结果，完美拟合了噪声标签，但仍然实现了合理的泛化。此外，对于高斯过程和(e) ResNet，边际似然（直接对应于PAC-Bayes边界[Germain等人，2016]）随着标签被篡改的程度增加而降低，如Wilson & Izmailov (2020)所述。下图：双下降现象。(f) ResNet和(g)线性随机特征模型都表现出双下降现象，在低训练损失区域，有效维度紧密跟踪第二次下降，如Maddox等人(2020)所述。

遵循Maddox et al. (2020)，我们在图1（底部）展示了ResNet-18和线性模型的双下降。对于ResNet，我们展示了随着每层宽度增加，CIFAR-100上的交叉熵损失。对于线性模型，我们展示了均方误差，该模型使用弱信息特征$y + \varepsilon$，其中$\varepsilon \sim \mathcal{N}(0, 1)$。两者都遵循类似的趋势：有效维度在插值区域之前增加，然后减小，此时泛化能力和有效维度一致。

图7. 神经网络损失景观中的模式通过曲线连接。ResNet-164在CIFAR-100上的$l_2$正则化交叉熵损失景观的三个不同的二维子空间，作为网络权重的函数。水平轴保持固定，锚定在两个独立训练网络的优化点上，而垂直轴在不同面板中变化。左图：传统假设中的孤立优化点。中和右图：优化点通过简单曲线连接，同时保持接近零损失的替代平面。模式连通性是深度神经网络相对独特的特性。图改编自Garipov等人(2018)。

也可以通过正式的PAC-Bayes界追踪双下降，如Lotfi et al. (2022a, 图7) 所示。在第二次下降中，更大的模型实现了相似的经验风险，但更具可压缩性。

7 替代观点

另一种观点认为，良性过拟合、双下降和过参数化主要是现代深度学习现象，需要重新思考泛化理论。

这种替代观点（相当主流！）最初是如何产生的呢？

偏差-方差权衡将期望的泛化损失分解为期望的数据拟合误差（偏差）和拟合结果之间的期望平方差（方差），基于数据生成分布进行分析。受限模型往往具有高偏差和低方差，而无约束模型则倾向于低偏差和高方差，这在双下降的经典区域中呈现出“U形曲线”。因此，教科书确实警告说：“一个训练误差为零的模型通常会对训练数据过拟合，并且泛化性能较差” [Hastie et al., 2017]。然而，“权衡”是一个误称：例如我们在第2节中提到的顺序依赖多项式模型，或者集成模型（[Bishop, 2006]；[Wilson & Izmailov, 2020]），都可以具有低偏差和低方差。

Rademacher复杂度衡量了一个函数类拟合均匀分布的±1标签的能力，对于表现出良性过拟合的模型，它无法提供有意义的泛化界限。类似的推理也适用于VC维度和fat-shattering维度。但在最近的回顾性研究中，例如“……仍然需要重新思考泛化”（[Zhang et al., 2021]），对PAC-Bayes的提及仅有一句话：“允许学习算法输出参数分布的情况下，也推导出了新的泛化界限”。正如我们在第3节中讨论的，PAC-Bayes和可数假设界限可以应用于确定性训练的模型。它们还提供了对这种泛化行为的严格概念性理解，并且已经存在了几十年。这些界限的基本思想甚至在知名教科书中也有描述，例如[Shalev-Shwartz & Ben-David, 2014, 第7.3章]。然而，这些框架似乎并未被广泛知晓或内化，而对大型网络的非空泛化界限直到后来才逐渐受到关注，例如在[Lotfi et al., 2022a]中。

神经网络的隐式正则化与我们在前面提到的顺序依赖正则化的高阶多项式示例不同。然而，这两种正则化都是软归纳偏差的例子，我们已经讨论了如何通过增加神经网络的规模来增强其隐式正则化。此外，这种隐式正则化反映在第3节讨论的泛化框架中，并通过有效维度等量来描述。隐式正则化也不仅限于神经网络，同样适用于第6节中的随机特征线性模型。此外，与传统观点相反，随机优化器的隐式正则化不太可能在深度学习的泛化中发挥主要作用，这一点在第5节中进行了讨论。另一方面，我们仍然处于理解规模和其他因素如何以及为何影响神经网络中隐式正则化的早期阶段。

总的来说，这些现象确实引人入胜，值得进一步研究。但它们并非无法用现有的泛化框架来描述，也并非是深度学习所独有的，尽管这种说法经常被提及。

8 有何不同或神秘之处？

如果这些现象并非深度神经网络所独有，那么什么才是呢？

深度神经网络确实与其他模型类别不同，并且在许多方面尚未被充分理解。仅其经验性能就使其脱颖而出。事实上，深度卷积神经网络与ImageNet上其他领先方法之间的显著性能差异，正是这一模型类别重新引起关注（并随后占据主导地位）的原因（Krizhevsky et al., 2012）。但如果它们并非通过过参数化、良性过拟合或双下降来区分，那么这些模型究竟有何不同？

在总结时，我们简要强调一些（但肯定不是全部）相对独特的神经网络性质和泛化行为。

8.1 表示学习

表示学习在很大程度上将神经网络与其他模型类别区分开来。表示学习到底意味着什么？

大多数模型类别可以表示为参数$w$和基函数$\phi$的内积：$f(x, w) = w^\top \phi(x)$。虽然函数类可能非常灵活（在某些情况下比我们可以在内存中拟合的任何神经网络更灵活）（Williams & Rasmussen, 2006），且基函数是非线性的，但基函数通常是先验固定的。例如，我们可能使用多项式基、傅里叶基或径向基。除了可能的一些超参数（如径向基的宽度）外，基函数通常没有许多从数据中学习的参数。相比之下，神经网络指定了一个自适应基：$f(x, w) = w^\top \phi(x, v)$，其中$v$是从数据中学习的一组相对较大的参数（神经网络的权重），它们通常通过涉及逐点非线性$\sigma$的连续矩阵乘法分层公式显著控制基函数的形状：$f(x, w) = W_{p+1}\sigma(W_p \dots \sigma(W_2\sigma(W_1 x)) \dots )$。这里，$\phi(x, v) = \sigma(W_p \dots \sigma(W_2\sigma(W_1 x)) \dots )$，且$v = W_1, \dots, W_p$。乍一看，学习基函数似乎没有必要。毕竟，正如我们在第5节中看到的，我们可以通过核函数实现所需的灵活性——具有固定基函数的通用逼近器。但通过学习基函数，我们实际上是在为特定问题学习核函数——一种相似性度量。能够学习相似性度量对于高维自然信号（图像、音频、文本等）至关重要，在这些信号中，欧几里得距离等标准相似性概念会失效。这种将表示学习视为相似性学习的观点超越了建模的标准基函数视角。例如，它也适用于$k$近邻（knn）等程序，其性能取决于选择固定的距离度量，而理想情况下，距离度量可以学习。

考虑一个表示学习的简单例子，假设我们希望预测人脸的朝向角度。具有相似朝向角度的人脸在像素强度上的欧几里得距离可能差异很大。但神经网络的内部表示可以学习到，对于当前任务，它们应该被类似地表示。换句话说，具有相似朝向角度的人脸在深层表示之间的欧几里得距离将相似，而不是在原始输入之间。这种学习相似性度量的能力对于外推——在远离数据的地方进行预测——是必要的。如果我们有足够密集分布的数据点用于插值，原始输入上的欧几里得距离是完全可以的：如果我们有许多59度和61度旋转的示例，插值将能很好地预测60度旋转。但通过表示学习，神经网络将能够从仅见过遥远角度的示例中准确预测60度旋转（Wilson et al., 2016）。

然而，表示学习并非神经网络独有。我们经常看到关于神经网络能做而核方法不能做的声明（例如，Allen-Zhu & Li, 2023）。几乎所有这些对比都隐含地假设核是固定的。但事实上，核学习是一个丰富的研究领域（Bach et al., 2004; Go ̈nen & Alpaydın, 2011; Wilson & Adams, 2013; Wilson et al., 2016; Belkin et al., 2018; Yang & Hu, 2020）。并且，没有必要将核方法与神经网络视为竞争关系。事实上，它们是高度互补的。核方法提供了一种使用具有无限基函数的模型的机制，而神经网络提供了一种自适应基函数的机制。我们没有理由不能拥有无限多个自适应基函数！深度核学习（Wilson et al., 2016）正是提供了这种桥梁，并最初在我们考虑的朝向角度问题上进行了演示。

这种方法最近因其仅需通过网络单次前向传播即可表示认知不确定性而重新引起关注。

神经网络也不是唯一进行表示学习的方式。例如，在低维空间中，通过在频谱密度上插值（学习数据的显著频率）作为核学习的一种机制可能很有效（Wilson & Adams, 2013; Benton et al., 2019）。

但神经网络是一种相对高效的学习自适应基函数的方式，尤其是在高维空间中。其原因尚不完全清楚。神经网络不仅学习了一种距离概念，而且这种距离度量会根据输入空间$x$中的位置而变化——它是非平稳的。非平稳度量学习在没有某些与数据良好对齐的假设的情况下是众所周知的困难（Wilson & Adams, 2013）。从根本上说，神经网络为数据提供了分层表示，而这些层次通常是现实世界问题的自然表示。正如我们将在第8.2节中讨论的那样，它们还提供了对低Kolmogorov复杂性的强烈偏好，这可能与自然数据分布良好对齐。

8.2 通用学习

历史上，传统观点是构建具有特定问题设置约束假设的专用学习器。例如，如果我们正在建模分子，我们可以硬编码旋转不变性——并与领域专家交流以了解我们希望在模型中施加的其他约束。这种方法通常受到“没有免费午餐定理”（Wolpert, 1996; Wolpert & Macready, 1997; Shalev-Shwartz & Ben-David, 2014）的启发，该定理表明，在均匀采样的所有数据集上，每个模型的期望性能是相同的。这些定理通常意味着，如果一个模型在一个问题上表现良好，它必须在其他问题上表现不佳，从而导致对高度定制假设的需求。

然而，深度学习的发展恰恰与这一传统观点相反！我们看到了模型的融合——从手工特征工程（SWIFT、HOG等），到特定领域的神经网络（用于视觉的CNN、用于序列的RNN、用于表格数据的MLP等），再到适用于一切的Transformer。这一结果可以通过神经网络模型和自然发生的数据分布（而非均匀采样的数据）对低Kolmogorov复杂性的偏好来解释。令人惊讶的是，即使是针对特定领域设计的模型，例如用于图像识别的卷积神经网络，由于其偏好，也被证明对完全不同的数据模态（例如表格数据）具有归纳偏差（Goldblum et al., 2024）。从一个训练好的神经网络开始，可以通过上界Kolmogorov复杂度，为其他问题甚至其他模态的性能推导出非空泛化界。

事实上，上下文学习（即模型在不更新其参数的情况下学习的能力）在神经网络中表现得尤为突出。在某种意义上，许多经典模型也在进行上下文学习或类似的操作：当我们使用具有固定RBF核的高斯过程，在某些训练数据上进行条件化，然后采样后验预测时，我们正在不更新模型表示的情况下进行条件生成。但Transformer在上下文学习中的相对通用性是前所未有的。例如，一个预训练用于文本补全的标准LLM，竟然能够与专门在时间序列数据上训练的时间序列模型相比，做出具有竞争力的零样本时间序列预测（Gruver et al., 2024）！

换句话说，神经网络不仅学习了数据的丰富表示，还学习了相对于其他模型类别而言在现实世界问题中相对通用的表示。我们强调，在上下文学习中，这些表示并不是固定的。在预训练期间，Transformer学会了学习，发现了诸如奥卡姆剃刀之类的归纳原则（Gruver et al., 2024; Goldblum et al., 2024）。在GP类比中，我们可以将预训练的Transformer视为具有不同核的大型GP专家混合体。基于下游数据集，Transformer根据预训练中学到的内容选择适当的核组合。

8.3 模式连通性

图7. 神经网络损失景观中的模式通过曲线连接。ResNet-164在CIFAR-100上的$l_2$正则化交叉熵损失景观的三个不同的二维子空间，作为网络权重的函数。水平轴保持固定，锚定在两个独立训练网络的优化点上，而垂直轴在不同面板中变化。左图：传统假设中的孤立优化点。中和右图：优化点通过简单曲线连接，同时保持接近零损失的替代平面。模式连通性是深度神经网络相对独特的特性。图改编自Garipov等人(2018)。

模式连通性是一种相对独特的神经网络现象（Garipov et al., 2018; Draxler et al., 2018; Frankle et al., 2020; Freeman & Bruna, 2017; Adilova et al., 2023）。如果我们用不同的初始化多次重新训练神经网络，传统观点认为我们会收敛到孤立的局部最优解，它们之间存在显著的损失障碍。然而，研究发现，这些不同解之间存在简单的路径，能够保持几乎为零的训练损失，如图7所示（Garipov et al., 2018; Draxler et al., 2018）。换句话说，将这些收敛解称为局部最优解甚至是一种误称！重要的是，模式连通路径上的参数设置对应于不同的函数，这些函数将在测试点上做出不同的预测，而不是表示模型规范中的退化性（如参数对称性）。

模式连通性对理解深度学习的泛化具有深远的意义。事实上，历史上对深度学习最常见的反对意见之一是损失景观（训练目标）的极端多模态性。模式连通性表明，我们在实践中找到的解都是相互连接的。因此，理解模式连通性并开发受这一现象启发的实用程序已成为一个活跃的研究领域（例如，Kuditipudi et al., 2019; Frankle et al., 2020; Benton et al., 2021; Zhao et al., 2020; Ainsworth et al., 2022）。

模式连通性还激发了流行的优化程序，如随机权重平均（SWA）（Izmailov et al., 2018），这反过来又启发了模型汤（Wortsman et al., 2022）和模型合并领域（Ainsworth et al., 2022; Yang et al., 2024）。

然而，与表示学习一样，模式连通性并非完全为神经网络所独有（例如，Kanoh & Sugiyama, 2024）。不过，模式连通性主要是一种深度学习现象，显然仅适用于复杂的非凸损失景观。

讨论

过参数化、良性过拟合和双下降是引人入胜的现象，值得进一步研究。然而，与广泛持有的观点相反，这些现象与理解泛化的长期框架一致，可以使用其他模型类复现，并且能够直观理解。展望未来，我们希望帮助不同研究群体走得更近，以便各种观点和泛化框架不被忽视。

图2. 泛化现象可以通过泛化边界进行形式化描述。泛化可以通过假设$h$的经验风险和可压缩性进行上界估计，如第3.1节所述。可压缩性以Kolmogorov复杂度$K(h)$形式化，可以进一步通过模型的文件大小进行上界估计。大模型能够很好地拟合数据，并且可以有效地压缩为较小的文件大小。与Rademacher复杂度不同，这些边界不会因为假设空间$H$能够拟合噪声而惩罚模型，并且描述了良性过拟合、双下降和过参数化现象。它们甚至可以为LLMs提供非空边界，如Lotfi等人(2024a)所述。

“Grokking”和扩展规律是近期备受关注的其他现象，同样引人入胜且值得进一步理解。但与本文讨论的现象不同，它们通常不被用作需要重新思考泛化框架或深度学习现象的证据。实际上，越来越多的研究表明，扩展规律和“Grokking”适用于线性模型（[Lin et al., 2024]；[Atanasov et al., 2024]；[Miller et al., 2023]；[Levi et al., 2023]）。重要的是，PAC-Bayes和可数假设界限也适用于大型语言模型（LLMs），如图2所示，近期的研究甚至表明这些界限能够描述Chinchilla扩展规律（[Finzi et al., 2025]）。

优化器在深度学习泛化中的作用是什么？

图6. 增加参数可以改善泛化。通过增加参数数量，平坦的解决方案（通常提供更简单且可压缩的数据解释）在总假设空间中占据更大的相对体积——这导致了对这些简单解决方案的隐式软归纳偏差。尽管过参数化模型通常表示许多过拟合数据的假设（例如参数设置），但它们可以表示更多拟合数据良好并提供良好泛化的假设。过参数化可以同时增加假设空间的大小和对简单解决方案的偏差。

传统观点认为，图6中的绿色和粉色区域实际上是颠倒的，深度学习之所以有效，是因为随机优化器的隐式偏好使它们能够在损失较小且泛化性能良好的解空间中进行搜索。然而，研究表明，不仅全批量梯度下降，甚至“猜测与检查”（随机采样参数向量并在损失低于阈值时停止）也能找到与随机优化具有类似泛化性能的解（[Geiping et al., 2021]；[Chiang et al., 2022]），这与图6（右侧）一致。尽管从理论上讲，优化器在这种损失景观下仍可能找到不良的最优解，但除非它具有对抗性，否则这种情况不太可能发生。实际上，随机优化确实具有能够改善泛化的偏好，但重要的是，这些偏好并非良好泛化的必要条件。当然，随机优化比其他替代方法在计算上更为实用。没有人建议我们使用“猜测与检查”！此外，开发在给定计算预算下泛化性能更好的优化器是一个特别令人兴奋的研究方向，尤其是近期关于二阶优化器的研究成果（[Liu et al., 2025]；[Vyas et al., 2024]）。最后，第3.1节中的泛化界限无论模型是否使用随机优化都可以进行评估，实际上这些界限能够追踪高斯过程的良性过拟合行为，而高斯过程执行的是贝叶斯推断。

结构风险最小化与软归纳偏差之间的关系是什么？

结构风险最小化（SRM）是一种编码软归纳偏差的方法，但它更狭窄且通常出于不同的动机。SRM通常用于降低VC维度，权衡数据拟合与模型复杂度之间的关系。它通常不被用作任意灵活模型的处方，实际上，与标准$l_2$正则化对应的模型选择工具表明，我们应该使用中间阶数的模型（[Bishop, 2006]）。本文的一个关键观点是，我们可以接受完美拟合数据（包括噪声）的模型，但仍然偏好简单性。实现软归纳偏差的其他方法包括过参数化、贝叶斯先验和边缘化、优化器以及架构设计。

我们如何更好地理解深度学习中的泛化？

深度学习泛化中有许多引人入胜的开放性问题。我们认为，分析神经网络实际达到的解以解释其行为是一种有前景的方法。第3.1节中的泛化界限是完全经验性的、非渐近的，并且可以使用单个样本进行评估。我们认为能够对界限进行经验评估对于确定理论实际上解释了多少模型行为至关重要。我们发现Solomonoff先验对于评估描述性泛化界限特别有用。Solomonoff归纳使用了一个最大化的过参数化模型，包含所有可能的程序，但它形式化了一个理想的学习系统，该系统为更短的程序赋予指数级更高的权重。未来，研究可能导致更紧密界限的先验属性，更接近描述深度学习泛化，将是富有启发性的。

致谢

我们感谢Shikai Qiu、Pavel Izmailov、Marc Finzi、Gautam Kamath、Micah Goldblum、Alan Amin、Jacob Andreas、Alex Alemi、Lucas Beyer、Mikhail Belkin、Sanae Lotfi、Martin Marek、Sanyam Kapoor、Patrick Lopatto、Preetum Nakkiran、Thomas Dietterich和Sadhika Malladi的有益讨论。这项工作得到了NSF CAREER IIS-2145492、NSF CDS&EMSS 2134216、NSF HDR-2118310、BigHat Biosciences、Capital One和亚马逊研究奖的部分支持。

A. 关于PAC-Bayes的常见误解

关于PAC-Bayes和可数假设界存在一些常见的误解。

误解：PAC-Bayes仅适用于随机网络，而不是我们在实践中使用的确定性训练网络，因为它刻画了后验样本的期望泛化。然而，后验不一定是贝叶斯后验，我们可以使用点质量后验和离散假设空间评估PAC-Bayes界：使用KL散度的相对熵定义，$KL(Q | P) = H(Q, P) - H(Q)$，交叉熵$H(Q, P)$变为$\log_2 \frac{1}{P(h)}$，而点质量$Q$的熵$H(Q)$或“惊讶度”为零，从而恢复与可数假设界非常相似的界。或者，可数假设界直接适用于确定性训练的模型。

误解：可数假设界不适用于具有连续参数的模型。我们使用的神经网络实际上是计算机上的程序，因此必须表示有限的假设空间。权重只能取有限数量的值，由精度（如浮点数）决定。一个相关的误解是，可数假设界必然很松，因为浮点神经网络参数值表示了许多假设。然而，界的形式表明，我们应避免严格测量假设数量，而应从先验可能性的角度理解泛化。事实上，这些界对于表示更多假设的更大模型可能更紧（Lotfi et al., 2024a）。

误解：随着参数数量的增加，这些界会变松。虽然许多界（包括一些PAC-Bayes界）确实有参数计数项（Jiang et al., 2019），但并非所有PAC-Bayes或可数假设界都是如此。事实上，最近的界随着模型参数数量的增加可能变得更紧（Lotfi et al., 2022a; 2024a;b），因为更大的模型可能具有更强的压缩偏好，导致界中的复杂性惩罚减少。

误解：紧的神经网络界仅适用于不现实的模型压缩。有一种称为压缩界的界，它刻画了参数被压缩到低维空间的模型的泛化。确实，这种方法在早期取得了成功，为更大数据集上的更大神经网络实现了非空界（Zhou et al., 2018; Lotfi et al., 2022a）。然而，有几个误解需要澄清：（1）所使用的压缩技术（例如形成参数空间的线性子空间）通常表现几乎与原模型一样好（Li et al., 2018）。这些界通常描述的是一个实际有吸引力的模型，而不是不现实的模型缩减；（2）将更大神经网络压缩到低维子空间的能力对泛化具有信息性；（3）最近的非空界并非压缩界，例如Lotfi et al. (2024b) 和Finzi et al. (2025) 中对数十亿参数LLM的界。

误解：Kolmogorov复杂度不可计算，因此基于Solomonoff先验的泛化界无法评估。无前缀Kolmogorov复杂度$K(h)$表示使用某种预定义编码表示$h$的最短程序的比特数。虽然我们无法计算最短程序，但我们可以通过模型的存储文件大小和一个由不依赖于数据的项（例如加载和运行模型的Python脚本的大小）给出的常数来上界最短程序。我们可以将这些不依赖于数据的常数项$A$吸收到Solomonoff先验中，通过处理$K(h\vert A)$。然后，我们可以通过训练模型的存储文件大小上界非无前缀（标准）Kolmogorov复杂度$C$（以$A$为条件），从而计算有信息性的泛化界。

顺便提一下，Kolmogorov复杂度的一个深刻特性是，它独立于所使用的编程语言或通用图灵机测量绝对信息。我们可以编写一个编译器，将一种语言的代码翻译成另一种语言，而无需参考任何特定字符串。特别是，不变性定理上界了任何两个通用图灵机下Kolmogorov复杂度的差异，差异由最短可能的编译器决定（Kolmogorov, 1965; Li & Vit ́anyi, 2008）。这样的编译器通常最多为几KB，与典型的ML数据集（可能为TB级）相比可以忽略不计。

误解：界仅在先验$P(h)$未被错误指定时成立。界并不要求先验用于生成正确的假设，或包含假设，甚至不要求先验被我们正在刻画的模型使用。它只是提供了一种计算界的机制。例如，如果界中使用的先验偏好简单解，而模型具有偏好复杂解的先验，我们只会得到一个较松的界。界的假设适用于我们正在使用的模型，包括Zhang et al. (2016) 的CIFAR良性过拟合实验。

B. 其他泛化框架

Rademacher复杂度（[Bartlett & Mendelson, 2002]）精确衡量了一个模型拟合均匀分布的${+1, -1}$随机噪声的能力。具体来说，假设空间$H$和输入样本${x_i, \dots, x_n}$的Rademacher复杂度定义为：

\[R(H) = \mathbb{E}_\sigma \left[ \sup_{h \in H} \frac{1}{n} \sum_{i=1}^{n} \sigma_i h(x_i) \right],\]

其中，$\sigma_i$是独立同分布的Rademacher随机变量（以相等概率取${+1, -1}$）。假设$h$的期望风险随后被限制为：

\[R(h) \leq \hat{R}(h) + 2R(H) + C,\]

其中$C$是由损失函数、样本量$n$以及置信度$1 - \delta$定义的常数。因此，如果模型的假设空间$H$能够拟合Rademacher噪声，则Rademacher泛化界限将变得没有信息量。

类似地，VC维度（[Vapnik et al., 1994]）衡量的是最大的整数$d$，使得假设空间$H$能够拟合（“打碎”）任意一组带有${+1, -1}$标签的$d$个点（例如，以所有$2^d$种可能的方式对这些点进行分类）。如果假设空间$H$的VC维度是$d$，则期望泛化误差被限制为：

\[R(h) \leq \hat{R}(h) + O\left( \sqrt{\frac{d \log(n)}{n}} \right).\]

因此，具有较大假设空间的模型具有没有信息量的VC泛化界限。

Fat-shattering维度（[Alon et al., 1997]）$fat_\gamma(H)$是对VC维度的改进，它通过某种裕度$\gamma$来拟合（“打碎”）标签（或者对于每个目标$y_i$，函数的所有可能值都在某个范围内$[y_i - \gamma, y_i + \gamma]$）。Fat-shattering维度与Rademacher复杂度密切相关：

\[R(H) \leq c_\gamma \sqrt{\frac{fat_\gamma(H)}{n}},\]

其中$c_\gamma$是与$\gamma$相关的常数。我们可以将期望泛化误差限制为：

\[R(h) \leq \hat{R}(h) + O\left( \sqrt{\frac{fat_\gamma(H) \log(n)}{n}} \right).\]

随着$\gamma$增大，fat-shattering维度$d$会减小，因为约束条件变得更难满足。如果模型只能以较小的$\gamma$（而不是更大的$\gamma$）拟合噪声，则可以通过fat-shattering维度来解释模型的噪声拟合能力和灵活的假设空间。然而，对于任意神经网络，fat-shattering维度通常难以计算。

表1. 泛化边界总结

我们在表1中提供了不同泛化界限的比较总结。

C. 可数假设界

定理C.1：考虑有界风险$R(h, x_i) \in [a, a + \Delta]$，以及一个可数假设空间$h \in \mathcal{H}$，对此我们有一个不依赖于${x_i}$的先验$P(h)$。设经验风险$\hat{R}(h) = \frac{1}{n} \sum_{i = 1}^{n} R(h, x_i)$是对于固定假设$h$，独立随机变量$R(h, x_i)$的和。设$R(h) = \mathbb{E}[\hat{R}(h)]$为期望风险。

至少以$1 - \delta$的概率有：

\[R(h) \leq \hat{R}(h) + \Delta\sqrt{\frac{\log 1/P(h) + \log 1/\delta}{2m}} \tag{5}\]

证明（[Lotfi 等人, 2024a]）。由于$m\hat{R}(h)$是独立且有界的随机变量之和，对于给定的假设$h$，我们可以应用霍夫丁不等式（[Hoeffding, 1994]）。对于任意$t > 0$：

\[\begin{align} P(R(h) \geq \hat{R}(h) + t) &= P(nR(h) \geq n\hat{R}(h) + nt)\\ P(R(h) \geq \hat{R}(h) + t) &\leq \exp(-2nt^2/\Delta^2) \end{align}\]

我们将根据$\exp(-2nt(h)^2/\Delta^2) = P(h)\delta$ ，为每个假设$h$选择不同的$t(h)$。

求解$t(h)$，可得：

\[t(h) = \Delta\sqrt{\frac{\log 1/P(h) + \log 1/\delta}{2n}} \tag{6}\]

这个界对于固定的假设$h$成立。然而，对于使用训练数据构建的$h^*({x})$ ，随机变量

\[\hat{R}(h^*) = \frac{1}{n} \sum_{i = 1}^{n} R(h^*(\{x\}), x_i)\]

不能分解为独立随机变量之和。由于$h^* \in \mathcal{H}$，如果我们能对任意$h$限制$R(h) \geq \hat{R}(h) + t(h)$的概率，那么这个界对于$h^*$也成立。

对事件$\bigcup_{h \in \mathcal{H}} [R(h) \geq \hat{R}(h) + t(h)]$取并集，我们有：

\[\begin{align} P(R(h^*) \geq \hat{R}(h^*) + t(h^*)) &\leq P\left(\bigcup_{h \in \mathcal{H}} [R(h) \geq \hat{R}(h) + t(h)]\right)\\ &\leq \sum_{h \in \mathcal{H}} P(R(h) \geq \hat{R}(h) + t(h))\\ &\leq \sum_{h \in \mathcal{H}} P(h)\delta = \delta \end{align}\]

因此，我们得出结论：对于任意$h$（无论是否依赖于$x$），至少以$1 - \delta$的概率有

\[R(h) \leq \hat{R}(h) + \Delta\sqrt{\frac{\log 1/P(h) + \log 1/\delta}{2n}}\]

$\square$

D. 实验细节

图1. 深度学习中出现的泛化现象可以通过简单的线性模型重现并得到理解。上图：良性过拟合。一个带有阶数相关正则化的150阶多项式能够合理地描述(a)简单和(b)复杂结构的数据，同时也能完美拟合(c)纯噪声。(d) 高斯过程完美重现了Zhang等人(2016)在CIFAR-10上的结果，完美拟合了噪声标签，但仍然实现了合理的泛化。此外，对于高斯过程和(e) ResNet，边际似然（直接对应于PAC-Bayes边界[Germain等人，2016]）随着标签被篡改的程度增加而降低，如Wilson & Izmailov (2020)所述。下图：双下降现象。(f) ResNet和(g)线性随机特征模型都表现出双下降现象，在低训练损失区域，有效维度紧密跟踪第二次下降，如Maddox等人(2020)所述。

在图1(a)(b)(c)中，我们使用一个150阶多项式，并带有与阶数相关的正则化项$\sum_{j} 2^{j} w_{j}^{2}$（绿色），来拟合由(a) $\sin(x)\cos(x^{2})$、(b) $x + \cos(\pi x)$、(c) $\mathcal{N}(0, 1)$噪声生成的回归数据。

图1. 深度学习中出现的泛化现象可以通过简单的线性模型重现并得到理解。上图：良性过拟合。一个带有阶数相关正则化的150阶多项式能够合理地描述(a)简单和(b)复杂结构的数据，同时也能完美拟合(c)纯噪声。(d) 高斯过程完美重现了Zhang等人(2016)在CIFAR-10上的结果，完美拟合了噪声标签，但仍然实现了合理的泛化。此外，对于高斯过程和(e) ResNet，边际似然（直接对应于PAC-Bayes边界[Germain等人，2016]）随着标签被篡改的程度增加而降低，如Wilson & Izmailov (2020)所述。下图：双下降现象。(f) ResNet和(g)线性随机特征模型都表现出双下降现象，在低训练损失区域，有效维度紧密跟踪第二次下降，如Maddox等人(2020)所述。

图1(d)(e)改编自[Wilson & Izmailov (2020)]，它使用了带有径向基函数（RBF）核的高斯过程，一个PreResNet - 20模型，各向同性先验$p(w) = \mathcal{N}(0, \alpha^{2}I)$以及拉普拉斯边缘似然，进而复现了[Zhang 等人 (2016)]中CIFAR - 10带噪声标签的实验。

图1. 深度学习中出现的泛化现象可以通过简单的线性模型重现并得到理解。上图：良性过拟合。一个带有阶数相关正则化的150阶多项式能够合理地描述(a)简单和(b)复杂结构的数据，同时也能完美拟合(c)纯噪声。(d) 高斯过程完美重现了Zhang等人(2016)在CIFAR-10上的结果，完美拟合了噪声标签，但仍然实现了合理的泛化。此外，对于高斯过程和(e) ResNet，边际似然（直接对应于PAC-Bayes边界[Germain等人，2016]）随着标签被篡改的程度增加而降低，如Wilson & Izmailov (2020)所述。下图：双下降现象。(f) ResNet和(g)线性随机特征模型都表现出双下降现象，在低训练损失区域，有效维度紧密跟踪第二次下降，如Maddox等人(2020)所述。

图1(f)改编自[Maddox 等人 (2020)]，使用了一个层宽度不断增加的ResNet - 18模型，在$\alpha = 1$的情况下测量训练损失、测试损失和有效维度。对于图1(g)，我们使用随机特征最小二乘模型$Xw = y$，其中$X_{i}$的每一列等于$y_{i} + \epsilon$，$\epsilon \sim \mathcal{N}(0, 1)$。我们测量均方误差（MSE），并在计算有效维度时使用$\alpha = 1$。

图2. 泛化现象可以通过泛化边界进行形式化描述。泛化可以通过假设$h$的经验风险和可压缩性进行上界估计，如第3.1节所述。可压缩性以Kolmogorov复杂度$K(h)$形式化，可以进一步通过模型的文件大小进行上界估计。大模型能够很好地拟合数据，并且可以有效地压缩为较小的文件大小。与Rademacher复杂度不同，这些边界不会因为假设空间$H$能够拟合噪声而惩罚模型，并且描述了良性过拟合、双下降和过参数化现象。它们甚至可以为LLMs提供非空边界，如Lotfi等人(2024a)所述。

图2改编自[Lotfi 等人 (2024a)]，针对各种规模的大语言模型（LLMs），评估了第3节中带有柯尔莫哥洛夫复杂度上界的可数假设界。

图5. 具有简单性偏差的灵活性适用于不同数据规模和复杂度的问题。我们使用2阶、15阶和正则化的15阶多项式来拟合由(a)-(c)描述的函数生成的三个不同训练数据规模的回归问题。我们使用一种特殊的正则化惩罚，该惩罚随着多项式系数的阶数增加而增加。我们展示了100次拟合的100个测试样本的平均性能±1个标准差。通过仅在需要时增加复杂度以拟合数据，正则化的15阶多项式在所有数据规模和不同复杂度问题上都优于或与其他模型相当。

图5将两个15阶多项式和一个2阶多项式拟合到由一个2阶多项式、一个15阶多项式和$\cos(\frac{3}{2}\pi x)$生成的数据上。其中一个15阶多项式使用了与阶数相关的正则化项$\sum_{j} 0.01^{2} j^{2} w_{j}^{2}$ 。训练和测试输入样本从$\mathcal{N}(0, 1)$中采样得到。测试位置的数量是100，训练样本的数量范围从10到100。对于每个训练样本大小，我们重新生成数据100次，并记录均方根误差（RMSE）及其标准差（用阴影表示）。[Goldblum 等人 (2024)]也展示了类似的结果。

所有其他图都是概念图。