044, k049, G057 3PSDF, Three-Pole Signed Distance Function for Learning Surfaces with Arbitrary Topologies

Zhangwenniu 于 2025-03-12 发布  |   阅读量: 次

论文链接

发表时间：

[v1] Tue, 31 May 2022 07:24:04 UTC (31,328 KB)

论文重点难点介绍

1 研究背景与动机

2 三极有符号距离函数（3PSDF）

3 实验验证

4 难点与解决方案

5 局限性

6 未来工作

论文详细讲解

论文详细解读：3PSDF: Three-Pole Signed Distance Function for Learning Surfaces with Arbitrary Topologies

1 研究背景

传统的神经隐式函数（如SDF）在3D形状学习中取得了显著进展，但它们通常仅限于封闭表面，因为需要明确区分空间的“内”和“外”。最近的研究通过无符号距离函数（UDF）来处理包含开放和封闭表面的复杂几何形状，但UDF存在以下问题：

为了解决这些问题，本文提出了三极有符号距离函数（3PSDF），能够表示任意拓扑结构的非封闭3D形状，并支持通过经典的Marching Cubes算法高效转换为网格。

2 三极有符号距离函数（3PSDF）

3PSDF的核心在于引入了一个新的“NULL”符号，除了传统的“内”（负值）和“外”（正值）符号。NULL符号用于标记空间中不存在表面的区域，并通过赋予nan值来阻止在这些区域形成决策边界。

2.1 定义

对于一个3D点 $p \in \mathbb{R}^3$，3PSDF将点映射到一个扩展的实数域：

\[\Psi(p) : \mathbb{R}^3 \to \{\mathbb{R}, \text{nan}\}\]

其中，nan表示NULL符号，用于消除不需要的表面。

2.2 场计算

对于非封闭表面，无法进行内外测试，因此作者利用表面法线来确定距离的符号。具体步骤如下：

1. 空间分解：将3D空间划分为局部单元格。

2. NULL区域：如果单元格不包含任何表面，则该单元格内的所有点被标记为NULL（nan）。

3. 距离计算：对于包含表面的单元格，计算查询点 $p_i$ 到最近表面点 $q_i$ 的距离 $d(p_i, S_i)$，并根据法线方向确定符号：

\[\Psi(p_i, S_i) = \begin{cases} d(p_i, S_i) & \text{if } n(q_i) \cdot \overrightarrow{q_ip_i} \geq 0 \\ -d(p_i, S_i) & \text{otherwise} \end{cases}\]

其中，$n(q_i)$ 是表面点 $q_i$ 的法线。

2.3 学习框架

由于NULL符号的存在，直接回归3PSDF的值会导致梯度消失问题。因此，作者提出了一个基于三分类的学习框架，将问题转化为对每个点分类为“内”、“外”或“NULL”。

\[\Phi_\theta(p, x) : \mathbb{R}^3 \times \mathcal{X} \to \{0, 1, 2\}\] \[L_B = \frac{1}{|B|N} \sum_{i=1}^{|B|} \sum_{j=1}^N \mathcal{L}(\Phi_\theta(p_{ij}, x_i), y_{ij})\]

其中，$y_{ij}$ 是点 $p_{ij}$ 的真实标签。

2.4 表面提取

在训练完成后，将预测的离散标签转换为3PSDF值：

使用Marching Cubes算法提取零等值面作为重建的网格。由于NULL值的存在，Marching Cubes会在没有形状的区域自然地停止提取表面。

3 实验验证

3.1 形状重建

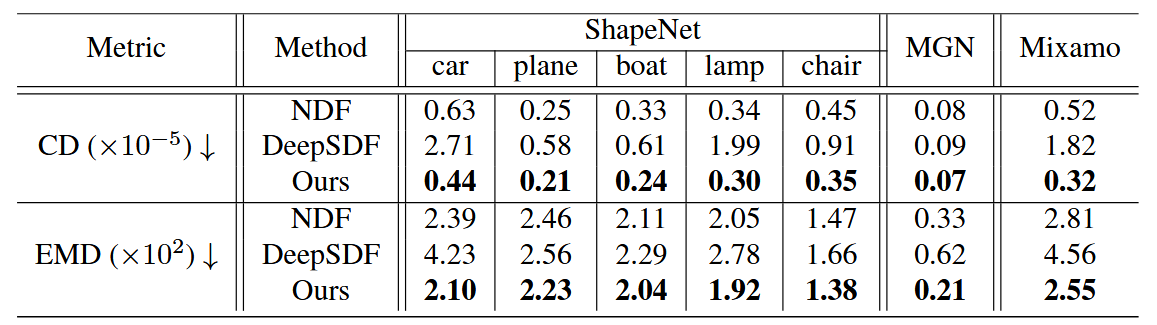
table.1

表1. 使用不同神经隐式表示的形状重建的定量比较。

作者通过与DeepSDF和NDF等现有方法的比较，验证了3PSDF在重建复杂几何形状（包括开放和封闭表面）时的优越性。实验结果表明，3PSDF能够更准确地重建细节，并在定量评估中取得了最佳性能。见表1。

3.2 从点云重建

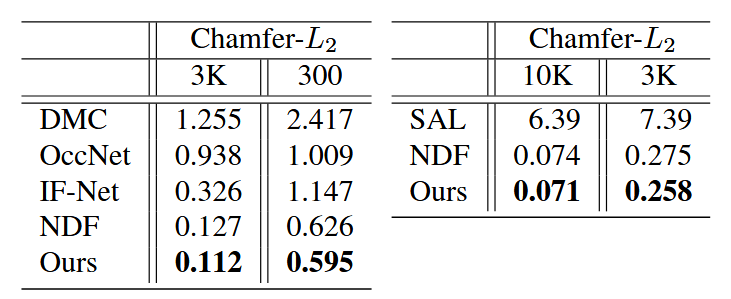
table.2

在稀疏点云条件下，3PSDF能够更好地重建包含内部结构和开放表面的复杂形状，而其他方法（如SAL和NDF）在处理开放表面时存在困难。见表2。

3.3 单视图重建

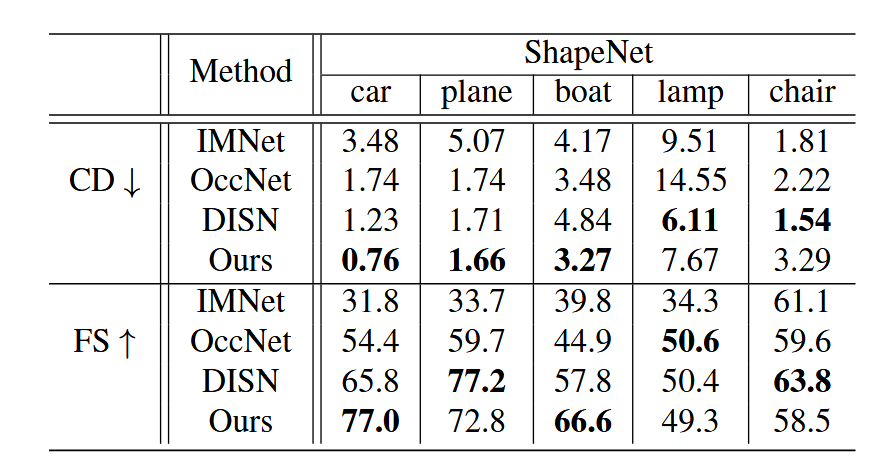
table.3

表3. 单视图重建的定量比较。Chamfer-L2和F-score分别以×10$^{-3}$和×10$^{-2}$报告。

3PSDF在单视图3D重建任务中表现出色，能够直接处理包含开放表面的原始形状，而无需将其转换为封闭表面。与IMNet、OccNet和DISN等方法相比，3PSDF在定量和定性评估中均取得了最佳性能。见表3。

4 局限性

5 未来工作

论文方法详解

1 三极有符号距离函数（3PSDF）的定义

3PSDF是一种新的隐式表示方法，通过引入“NULL”符号，扩展了传统的有符号距离函数（SDF），从而能够表示包含开放表面的复杂几何形状。

具体定义为：

\[\Psi(p) : \mathbb{R}^3 \to \{\mathbb{R}, \text{nan}\}\]

其中，点 $p$ 被映射到一个实数值或nan（表示NULL符号）。NULL符号用于消除不需要的表面，从而支持任意拓扑结构的表示。

2 场计算（Field Computation）

为了计算3PSDF，作者提出了基于局部单元格的分解方法，并利用表面法线来确定距离的符号。具体步骤如下：

1. 空间分解：将3D空间划分为局部单元格（cells）。

2. NULL区域处理：如果单元格 $C_i$ 不包含任何表面，则该单元格内的所有点被标记为NULL区域：

\[\Psi(p_i, S) = \text{nan}, \quad \text{if } p_i \in C_i \text{ and } C_i \cap S = \emptyset\]

3. 距离计算与符号确定：对于包含表面的单元格 $C_i$，计算查询点 $p_i$ 到最近表面点 $q_i$ 的距离 $d(p_i, S_i)$，并根据法线方向确定符号：

\[\Psi(p_i, S_i) = \begin{cases} d(p_i, S_i), & \text{if } n(q_i) \cdot \overrightarrow{q_i p_i} \geq 0 \\ -d(p_i, S_i), & \text{otherwise} \end{cases}\]

其中，$n(q_i)$ 是表面点 $q_i$ 的法线方向。

3 学习框架（Learning Framework）

3PSDF的学习框架将问题转化为一个三分类任务，从而避免了由于NULL符号导致的梯度消失问题。具体如下：

1. 三分类任务：将每个点分类为“内”（inside）、“外”（outside）或“NULL”（null）。

网络的目标是学习一个映射函数：

\[\Phi_\theta(p, x) : \mathbb{R}^3 \times \mathcal{X} \to \{0, 1, 2\}\]

其中，$p$ 是点坐标，$x$ 是输入观测（如点云或图像），输出为离散标签（0：内，1：外，2：NULL）。

2. 训练过程：使用交叉熵损失函数进行训练。对于每个样本 $x_i$，从其对应的3D形状中采样 $N$ 个点 $p_{ij}$，计算损失：

\[L_B = \frac{1}{|B|N} \sum_{i=1}^{|B|} \sum_{j=1}^N \mathcal{L}(\Phi_\theta(p_{ij}, x_i), y_{ij})\]

其中，$y_{ij}$ 是点 $p_{ij}$ 的真实标签。

3. 八叉树细分（Octree-based Subdivision）：为了提高重建精度并减少计算复杂度，作者采用八叉树细分方法。仅对与输入形状相交的单元格进行细分，随着细分深度增加，每个单元格包含的几何复杂度降低，从而提高近似精度。

4 表面提取（Surface Extraction）

在训练完成后，将预测的离散标签转换为3PSDF值：

随后，使用经典的Marching Cubes算法提取零等值面作为重建的网格。由于NULL值的存在，Marching Cubes会在没有形状的区域自然地停止提取表面，从而避免生成伪表面。

5 方法的优势

1. 表示能力：通过引入NULL符号，3PSDF能够表示任意拓扑结构的3D形状，包括开放和封闭表面。

2. 训练效率：三分类任务避免了梯度消失问题，使得网络更容易训练。

3. 网格生成效率：与UDF的Ball Pivoting算法相比，3PSDF可以直接利用Marching Cubes算法高效生成高质量的网格。

6 局限性

1. 多层表面重建：在重建非常接近的多层表面时，3PSDF需要更高的采样密度来插入NULL层，否则可能会生成伪表面。

2. 训练时间：由于3PSDF的表示能力增强，训练时需要更丰富的特征和更长的训练时间，尤其是在使用单视图图像作为输入时。

论文关键点解析

\(x\in X\)作为额外输入

When applying such a network for downstream tasks (e.g. 3D reconstruction) based on observation of the object (e.g. point cloud, image, etc.), the network must be conditioned on the input. Therefore, in addition to the coordinate of points \(p \in R^3\), the network also consumes the observation of object \(x \in \mathcal{X}\) as input. Specifically, such a mapping function can be parameterized by a neural network \(\Phi_\theta\) that takes a pair \((p, x)\) as input and outputs its 3-class label

在论文中，\(\mathcal{X}\) 表示输入观测数据的集合，具体取决于任务类型。它为网络提供了关于目标形状的附加信息，帮助网络更好地预测3PSDF值。根据不同的任务，\(\mathcal{X}\) 可以有以下几种含义：

1. 点云（Point Cloud）：

当任务是从点云重建3D形状时，\(\mathcal{X}\) 是输入的点云数据。这些点云可以是稀疏的，包含了目标形状的部分或全部表面信息。网络通过这些点云数据学习形状的几何特征。

2. 图像特征（Image Features）：

在单视图重建（Single-View Reconstruction）任务中，\(\mathcal{X}\) 是从输入图像中提取的特征。例如，可以使用预训练的卷积神经网络（如VGG16）提取图像的特征向量，这些特征向量作为网络的输入，帮助网络从单张图像重建出3D形状。

3. 其他观测数据：

在某些情况下，\(\mathcal{X}\) 也可以是其他形式的观测数据，例如多视图图像的特征融合、深度图或其他与目标形状相关的数据。

总结来说，\(\mathcal{X}\) 是网络的附加输入，用于提供关于目标形状的上下文信息，帮助网络更好地理解输入点 \(p \in \mathbb{R}^3\) 在全局几何中的位置和关系。

原文翻译

3PSDF：用于学习任意拓扑表面的三极符号距离函数

Weikai Chen, Cheng Lin, Weiyang Li, Bo Yang

腾讯游戏数字内容技术中心

{weikaichen,arnolin,kimonoli,brandonyang}@tencent.com

摘要

近期使用神经隐式函数学习3D形状的进展取得了令人印象深刻的成果，通过突破之前在分辨率和多样性方面对不同拓扑结构的限制。然而，大多数此类方法仅限于封闭表面，因为它们要求空间被划分为内部和外部。最近基于无符号距离函数的工作已被提出来处理同时包含开放和封闭表面的复杂几何体。尽管如此，由于它们的直接输出是点云，从离散点稳健地获取高质量网格结果仍然是一个开放性问题。我们提出了一种新颖的可学习隐式表示，称为三极符号距离函数(3PSDF)，它可以表示具有任意拓扑结构的非水密3D形状，同时支持使用经典的Marching Cubes算法进行简便的场-网格转换。我们方法的关键是引入了一个新的符号——NULL符号，作为传统的内部和外部标签的补充。NULL符号的存在可以阻止由内部/外部区域的二等分线导出的封闭等值面的形成。此外，我们提出了一个专门的学习框架，以有效地学习3PSDF，而不必担心由于NULL标签导致的梯度消失问题。实验结果表明，我们的方法在广泛的基准测试中在定量和定性方面都优于之前的最先进方法。

1 引言

3D形状和表面表示的选择一直是有效3D学习的核心话题。过去几年中，各种3D表示方法，包括网格[18,41]、体素[36,42]和点云[31,32]，已被广泛研究。近期，神经隐式函数(NIF)[6,20,26,29]的出现为基于学习的3D重建和建模的最新技术带来了令人印象深刻的进步。经典的NIF方法建立在符号距离函数(SDF)之上；它们训练深度神经网络通过占用预测或回归SDF来将连续的3D位置分类为表面内部或外部。然而，它们只能建模支持水平面提取的内/外测试的封闭表面。

fig.3

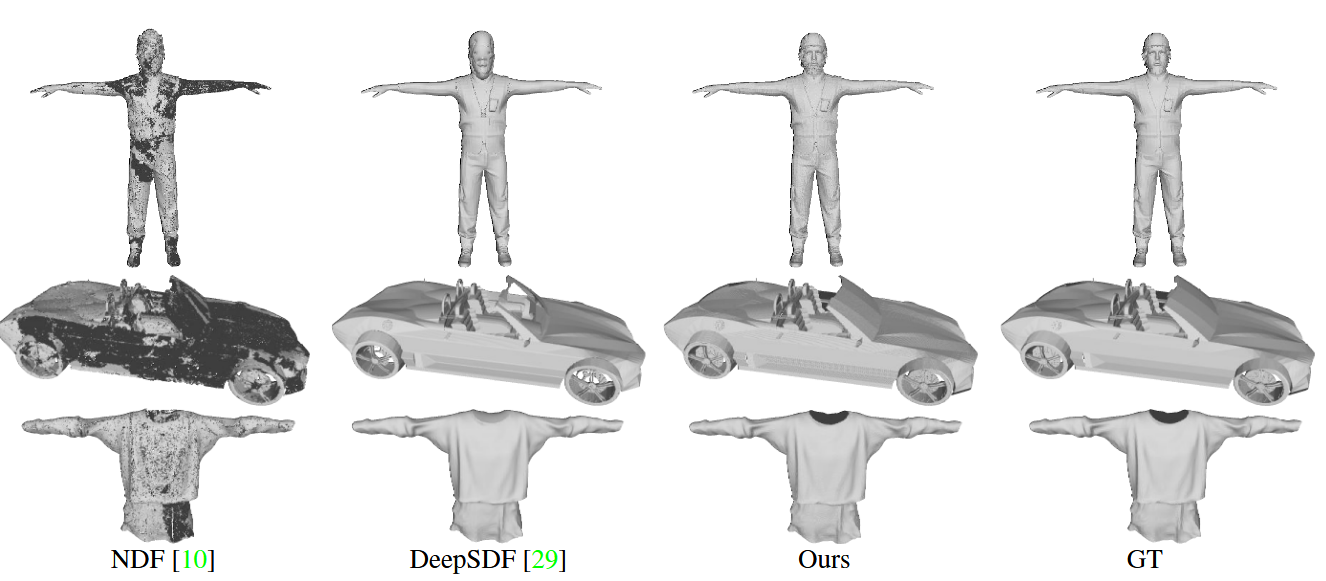
图3. 使用不同神经隐式表示的形状重建结果的视觉比较。

fig.1

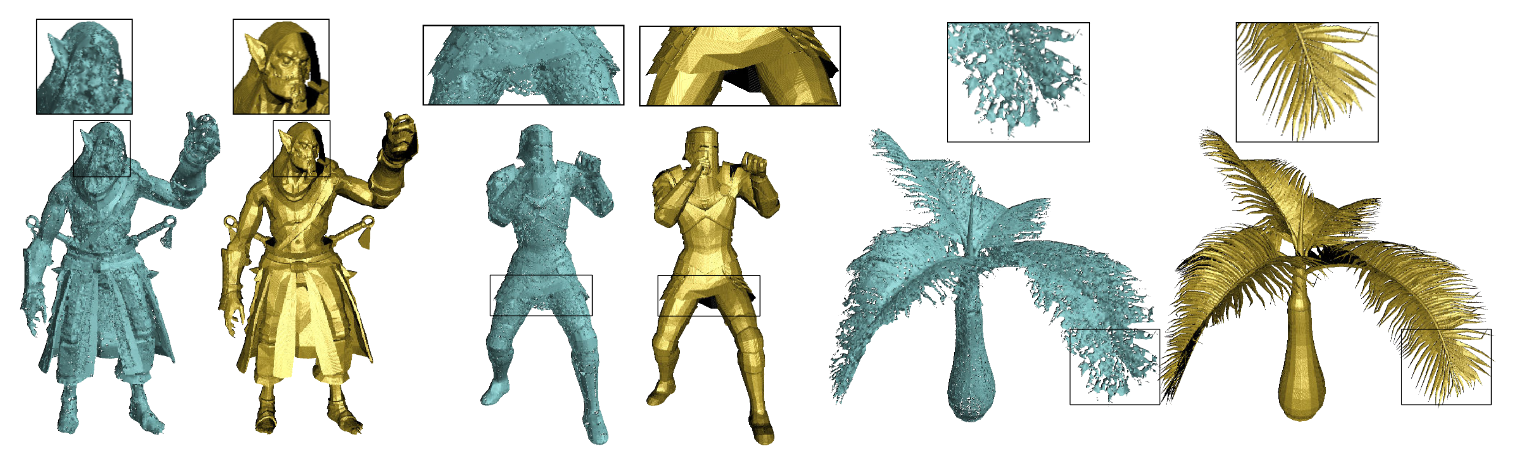
图1. 我们展示了由NDF [10]（青色）和我们提出的3PSDF（金色）分别生成的三组形状重建结果。我们的方法能够忠实地重建高保真、复杂的几何细节，包括封闭和开放表面，而NDF则存在网格化问题。每个NDF结果都是从包含100万个点的密集点云重建的，而我们的结果则是使用等效分辨率重建的。

最近利用无符号距离函数(UDF)[10,39,40]的进展使得从点云学习开放表面成为可能。但将此场实例化为显式网格仍然繁琐且容易产生伪影。它需要生成密集点云并利用UDF的梯度场迭代地将点推到目标表面上。这种过程容易受到复杂梯度景观的影响，例如有许多细节的部分，并且容易陷入局部最小值。此外，从UDF重建网格必须使用球旋转(BP)算法，该算法有几个缺点：1) 它对输入球半径非常敏感。稍大或稍小的半径都会导致不完整的网格结果。2) 即使对于中等复杂度的表面，它也容易生成自相交和具有不一致法线的断开的面片（见图3中的服装结果）。3) BP算法非常耗时，尤其是处理密集点云时。最后，学习UDF变成了回归任务而不是像SDF那样的分类，使训练更加困难。我们在图1的特写中显示，即使有100万个采样点，NDF[8]也无法重建第一个角色的面部细节。

fig.1

图1. 我们展示了由NDF [10]（青色）和我们提出的3PSDF（金色）分别生成的三组形状重建结果。我们的方法能够忠实地重建高保真、复杂的几何细节，包括封闭和开放表面，而NDF则存在网格化问题。每个NDF结果都是从包含100万个点的密集点云重建的，而我们的结果则是使用等效分辨率重建的。

我们通过提出一种新的可学习隐式表示，称为三极符号距离函数(3PSDF)，克服了上述限制，该函数能够以高保真度表示包含封闭和开放表面的高度复杂几何体（见图1）。此外，3PSDF使学习成为易于训练的分类任务，并且与经典高效的等值面提取技术兼容，例如Marching Cubes算法。

fig.2

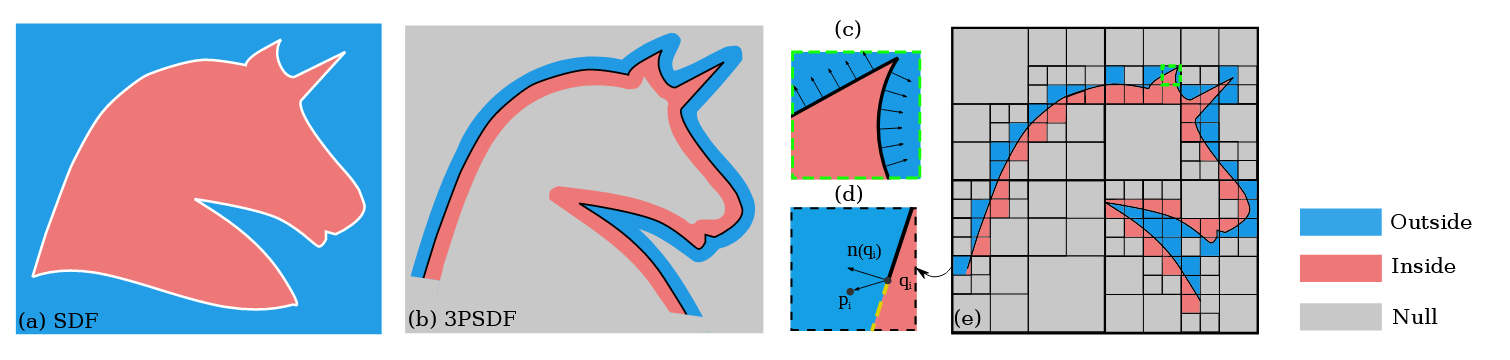
图2. 3PSDF的二维示意图。(a) 传统的符号距离函数（SDF）只能表示封闭表面。(b) 通过将零符号引入SDF，3PSDF可以禁用指定的决策边界以生成包含开放表面的任意拓扑。我们提出了基于局部单元的3PSDF计算框架（(c)和(d)）。虽然3PSDF可能会为单元内的开放表面引入近似误差（(d)中的黄色虚线），但通过更精细的空间分解可以显著减少近似误差。我们提出了基于八叉树的细分方法（e），以提高计算效率的近似性能。

我们方法的关键思想是在传统的二元符号距离函数中引入一个无方向的符号——NULL符号。具有null符号的点将被赋予nan值，防止在它们与其邻居之间形成决策边界。因此，通过适当地在空间中分布null符号，我们能够铸造具有任意拓扑结构的表面（见图2）。与之前基于占用预测的工作[6,26]类似，我们训练神经网络将连续点分类为3类：内部、外部和null。得到的标签可以使用简单的映射函数转换回3PSDF以获得网格结果。

我们在三个难度逐渐增加的任务上评估3PSDF：形状重建、点云补全和单视图重建。3PSDF在广泛的基准测试中，包括ShapeNet[5]、MGN[4]、Maximo[1]和3D-Front[16]，在定量和定性方面都能持续优于最先进的方法。我们还进行了与NDF的场到网格转换时间的比较，并分析了不同分辨率和采样策略对我们方法的影响。

我们的贡献可以总结为：

• 我们提出了一种新的可学习3D表示，3PSDF，它可以表示具有封闭和开放表面的高度复杂形状，同时与现有的水平面提取技术兼容。

• 我们为3PSDF提出了一种简单而有效的学习范式，使其能够处理像单视图重建这样具有挑战性的任务。

• 我们使用3PSDF在广泛的基准测试中的三个应用上获得了最先进的结果。

2 相关工作

使用显式表示的学习

3D形状的显式表示通常是规范化和结构化的。基于体素的方法[11,17,19]与卷积神经网络兼容，便于学习；为了减少高内存成本，采用了基于八叉树的分区[23,36,42]。然而，物体的内部通常占据了大部分体素，由于内存限制导致3D精度受到影响。基于网格的方法主要是变形预定义的网格来近似给定的3D形状[14,18,28,41]。这类方法的一个关键限制是改变网格拓扑结构的困难，限制了其3D表示能力。点云最近受到了很多关注[32,33,38,44]，因为其简单性。尽管这些方法便于形状分析，但生成高精度的3D形状仍然困难。

隐式函数学习

随着深度学习的发展，3D形状的隐式表示在近年来取得了巨大进步[6,8,15,24,27,35]。一个很好的例子是符号距离场(SDF)，它在3D空间中创建连续的隐式场[29,30]，其中外部和内部点分别由正负SDF表示。零等值面，即物体的表面，可以通过Marching Cubes[25]高效提取。这种表示支持无限分辨率，并且可以将SDF学习简化为二元分类过程[26]。然而，SDF仅适用于具有封闭表面的物体。

为了处理开放表面，提出了无符号距离场(UDF)[10]和深度无符号距离嵌入[40]。这些方法使用绝对距离来描述点位置，零等值面通过Ball-Pivoting算法[3]提取。然而，它们有几个主要限制：1) 学习UDF是一个回归问题，比SDF中的更难；2) ball pivoting[3]比Marching Cubes[25]计算成本更高且稳定性更差；3) 梯度在表面上消失，导致伪影。Venkatesh等人[39]提出了最近表面点(CSP)表示，以防止梯度消失并提高速度。Zhao等人[45]提出了Anchor UDF来提高重建精度。然而，UDF类型方法的前两个限制仍然存在。

3 三极有向距离函数

3.1 定义

一个水密的三维形状可以通过有向距离函数隐式表示。给定一个三维查询点 $\mathbf{p} \in \mathbb{R}^3$，先前的研究工作应用深度神经网络，要么将 $\mathbf{p}$ 的占据情况预测为 $f(\mathbf{p}): \mathbb{R}^3 \mapsto [0, 1]$ [20]，要么直接回归有向距离函数（SDF）为 $f(\mathbf{p}): \mathbb{R}^3 \mapsto \mathbb{R}$ [29, 43]。我们的关键观察是，只要空间中同时存在正号和负号（注意，我们不考虑仅在有限边界区域内计算SDF的空间裁剪情况），封闭表面的形成就是不可避免的。为了解决这个问题，我们在该领域引入第三个无方向的极——NULL符号，这样封闭性的 “限制” 就可以解除：在正/NULL 或负/NULL 对的平分线上不会形成等值面。因此，NULL符号充当了表面消除器，它可以消除不需要的表面，从而能够灵活地表示任意拓扑结构，包括那些具有开放表面的结构。

形式上，对于三维点 $\mathbf{p} \in \mathbb{R}^3$，我们提出，除了连续的有向距离外，它还可以映射到空值：$\Psi(\mathbf{p}): \mathbb{R}^3 \mapsto {\mathbb{R}, nan}$。因此，给定一个输入表面 $\mathcal{S}$，我们的目标是学习这样一个映射函数 $\Psi$，使得

\[\underset{\Psi}{\text{argmin}} \|\mathcal{S} - \mathcal{M}(\Psi(\mathbf{p}))\|, \tag{1}\]

其中 $\mathcal{M}$ 是一个网格化算子，它将结果场转换为显式表面，而 $|\cdot|$ 返回表面到表面的距离。接下来，我们将介绍如何为给定的形状计算相应的三极有向距离函数（3PSDF）。

3.2 场计算

fig.2

图2. 3PSDF的二维示意图。(a) 传统的符号距离函数（SDF）只能表示封闭表面。(b) 通过将零符号引入SDF，3PSDF可以禁用指定的决策边界以生成包含开放表面的任意拓扑。我们提出了基于局部单元的3PSDF计算框架（(c)和(d)）。虽然3PSDF可能会为单元内的开放表面引入近似误差（(d)中的黄色虚线），但通过更精细的空间分解可以显著减少近似误差。我们提出了基于八叉树的细分方法（e），以提高计算效率的近似性能。

对于没有封闭边界的非水密表面，无法对查询点进行 “内部/外部” 测试。因此，我们利用表面法向量来确定距离的符号。具体来说，我们将三维空间分解为局部单元格网格。如图2所示，对于每个单元格 $\mathcal{C}_i$，如果它不包含任何感兴趣的表面，我们将其封闭空间设置为空区域，并且位于 $\mathcal{C}_i$ 内部的任何采样点 $\mathbf{p}_i$ 到目标表面 $\mathcal{S}$ 的距离为非数值（nan）：

\[\Psi(\mathbf{p}_i, \mathcal{S}) = nan, \text{ if } \mathbf{p}_i \in \mathcal{C}_i \text{ and } \mathcal{C}_i \cap \mathcal{S} = \varnothing \tag{2}\]

对于包围一个表面片 $\mathcal{S}_i$ 的局部单元格 $\mathcal{C}_i$，给定查询点 $\mathbf{p}_i \in \mathcal{C}_i$，我们在 $\mathcal{S}_i$ 上找到 $\mathbf{p}_i$ 的最近点 $\mathbf{q}_i$。我们将 $\mathbf{q}_i$ 处的表面法向量设为 $\mathbf{n}(\mathbf{q}_i)$。如果向量 $\overrightarrow{\mathbf{q}_i\mathbf{p}_i}$ 与 $\mathbf{n}(\mathbf{q}_i)$ 同向，即 $\mathbf{n}(\mathbf{q}_i) \cdot \overrightarrow{\mathbf{q}_i\mathbf{p}_i} \geq 0$，我们将 $\mathbf{p}_i$ 到输入表面 $\mathcal{S}$ 的距离设为正；否则，设为负。计算过程可以总结如下：

\[\Psi(\mathbf{p}_i, \mathcal{S}_i)= \begin{cases} \mathbf{d}(\mathbf{p}_i, \mathcal{S}_i) & \text{if } \mathbf{n}(\mathbf{q}_i) \cdot \overrightarrow{\mathbf{q}_i\mathbf{p}_i} \geq 0, \\ -\mathbf{d}(\mathbf{p}_i, \mathcal{S}_i) & \text{otherwise}, \end{cases} \tag{3}\]

其中 $\mathbf{d}(\mathbf{p}, \mathcal{S}_i)$ 返回 $\mathbf{p}_i$ 与 $\mathcal{S}_i$ 之间的绝对距离。随着对三维空间更精细的分解，包含几何信息的单元格将仅分布在感兴趣的表面周围，而空单元格将占据大部分空间。这与传统的有向距离场有很大不同，在传统有向距离场中，整个空间都被正号或负号的距离值填满。我们提出的三极有向距离函数（3PSDF）更好地反映了任何拓扑结构的三维表面的本质——表面占据的高稀疏性。

表面近似能力

fig.2

图2. 3PSDF的二维示意图。(a) 传统的符号距离函数（SDF）只能表示封闭表面。(b) 通过将零符号引入SDF，3PSDF可以禁用指定的决策边界以生成包含开放表面的任意拓扑。我们提出了基于局部单元的3PSDF计算框架（(c)和(d)）。虽然3PSDF可能会为单元内的开放表面引入近似误差（(d)中的黄色虚线），但通过更精细的空间分解可以显著减少近似误差。我们提出了基于八叉树的细分方法（e），以提高计算效率的近似性能。

如果一个封闭表面将其所在的单元格细分为几个封闭的子区域，我们的隐式表示可以在不损失精度的情况下忠实地近似原始形状（图2(c)）。如果一个局部单元格包含突出的开放表面，我们的方法可能会生成细长的表面片（图2(d)）。然而，这种近似误差仅在局部出现，并且局限于局部单元格的大小。因此，通过更密集的三维分解，我们可以显著降低近似误差。我们在4.5节中提供了额外的实验，展示了不同采样分辨率下的重建性能。

3.3 学习框架

尽管NULL符号的引入为消除不需要的表面提供了灵活性，但非数值（nan）值阻碍了计算更新深度神经网络所需的有意义梯度。为了解决这个问题，一种直接的方法是结合二分类（nan与非nan）和回归，前者生成表面周围有效窄带的掩码，后者在这个窄带内对表面进行回归。虽然我们通过实验验证了可以通过这种方法学习三极有向距离函数（3PSDF），但在对齐来自二分类的窄带掩码和来自回归分支的回归决策边界时会出现额外的挑战。两个分支结果的不对齐会导致最终重建出现不连续性。因此，我们提出了一种替代的学习框架，将3PSDF的学习表述为一个三分类问题，具体阐述如下。我们在主论文中介绍了三分类框架的方法和结果，在补充材料中提供了两种学习方法的详细比较。

与先前关于占据预测的研究工作[6, 26]类似，三分类方法建议使用一个推断逐点标签 ${in, out, null}$ 的神经网络来近似目标函数（公式2和3）。我们使用离散数字表示标签语义，且不失一般性。形式上，我们旨在学习一个映射函数 $o: \mathbb{R}^3 \mapsto {0, 1, 2}$，其中标签 ${0, 1, 2}$ 分别表示内部、外部和NULL。

当将这样一个网络应用于基于对象观测（例如点云、图像等）的下游任务（如三维重建）时，该网络必须以输入为条件。因此，除了点 $\mathbf{p} \in \mathbb{R}^3$ 的坐标外，网络还将对象观测 $\mathbf{x} \in \mathcal{X}$ 作为输入。具体来说，这样一个映射函数可以由一个神经网络 $\Phi_{\theta}$ 参数化，它将一对 $(\mathbf{p}, \mathbf{x})$ 作为输入并输出其三分类标签：

\[\Phi_{\theta}(\mathbf{p}, \mathbf{x}): \mathbb{R}^3 \times \mathcal{X} \mapsto \{0, 1, 2\}. \tag{4}\]

训练：为了学习神经网络 $\Phi_{\theta}(\mathbf{p}, \mathbf{x})$ 的参数 $\theta$，我们使用批量点样本对网络进行训练。对于训练批次中的第 $i$ 个样本，我们采样 $N$ 个点 $p_{ij} \in \mathbb{R}^3, j = 1, \ldots, N$。小批量损失 $\mathcal{L}_{\mathcal{B}}$ 为：

\[\mathcal{L}_{\mathcal{B}} = \frac{1}{|\mathcal{B}|N} \sum_{i = 1}^{|\mathcal{B}|} \sum_{j = 1}^{N} \mathcal{L}(\Phi_{\theta}(p_{ij}, x_{i}), y_{ij}), \tag{5}\]

其中 $\mathcal{L}(\cdot, \cdot)$ 计算交叉熵损失，$x_{i}$ 是批次 $\mathcal{B}$ 的第 $i$ 个观测值，$y_{ij}$ 表示点 $p_{ij}$ 的真实标签。

基于八叉树的细分

fig.2

图2. 3PSDF的二维示意图。(a) 传统的符号距离函数（SDF）只能表示封闭表面。(b) 通过将零符号引入SDF，3PSDF可以禁用指定的决策边界以生成包含开放表面的任意拓扑。我们提出了基于局部单元的3PSDF计算框架（(c)和(d)）。虽然3PSDF可能会为单元内的开放表面引入近似误差（(d)中的黄色虚线），但通过更精细的空间分解可以显著减少近似误差。我们提出了基于八叉树的细分方法（e），以提高计算效率的近似性能。

由于三极有向距离函数（3PSDF）的计算是局部进行的，为了确保较高的重建精度，最好不要在一个单元格中包含过多复杂的几何细节和开放表面。我们提出一种基于八叉树的细分方法[37, 42]，如图2(e)所示。仅当局部单元格与输入形状相交时，我们才对其进行细分。随着细分深度的增加，每个局部单元格所包含的表面片的复杂度会降低，从而实现更高的近似精度。此外，由于不包含形状的区域不会进一步细分，我们能够在计算复杂度和重建精度之间取得平衡。在我们所有的实验中，除非另有说明，我们都使用基于八叉树的细分来计算真实值。我们在4.5节中的实验验证了基于八叉树采样在性能上的优势。

3.4 表面提取

一旦网络学习完成，我们能够用我们的预测标记每个查询点。为了提取等值面，我们首先将推断的离散标签转换回原始3PSDF表示。标签为0、1和2的点分别被赋予SDF值-1、1和nan。然后可以将重建的表面提取为零水平面。注意，由3PSDF表示的等值面可以直接使用经典的Marching Cubes (MC)算法提取。null值的存在会自然地防止MC在不包含形状的位置提取有效的等值面。同时，在目标表面附近，等值面提取可以像传统的符号距离场一样正常进行。在MC计算之后，我们只需要移除由null立方体生成的所有nan顶点和面。剩余的顶点和面作为网格结果。

4 实验

4.1 实验设置

任务和数据集。我们使用三种类型的实验验证所提出的3PSDF。首先，我们通过检查3PSDF如何从学习的潜在嵌入重建复杂的3D形状来分析3PSDF的表示能力。这给了我们在其他输入条件下可以达到的结果的上限。其次，我们将3PSDF的学习条件设为稀疏点云，并通过输入3D特征来测试其性能。最后，我们使用图像特征作为输入，并在具有挑战性的单视图重建任务上提供验证。所有实验都与最先进的方法进行比较，以便更好地验证。实验在广泛的3D数据集上进行，包括ShapeNet[5]、MGN[4]、3D-Front[16]和Maximo[1]。具体设置在以下实验中详细说明。

实现细节。对于从点云重建的任务，我们使用与NDF[10]相同的点编码器(IF-Net)和超参数。对于单视图重建，我们使用带有批量归一化的VGG16[34]作为图像编码器。与DISN[43]类似，我们使用多尺度局部和全局特征来预测3PSDF值。我们基于可见性[13]重新定向地面真值表面的法线，使它们保持一致。我们通过填充小孔和平滑表面来优化结果。地面真值3PSDF值以$128^3$的分辨率生成，结果使用$256^3$的分辨率进行评估。我们对所有实验使用基于八叉树的重要性采样。为了简化3PSDF的学习，我们通过对所有样本使用统一的边界框，确保最小叶八叉树单元的大小在不同对象之间保持一致。

4.2 形状重建

为了评估3PSDF建模复杂几何体的能力，我们进行了形状重建实验，与其他最先进的神经隐式表示方法进行比较：DeepSDF[29]和NDF[10]。类似于[29]中的自动编码方法，我们将每个训练样本嵌入到512维潜在编码中，并训练神经网络从嵌入中重建3D形状。我们在ShapeNet的五个包含最复杂几何体的代表性类别上进行评估，以及两个具有开放表面的数据集：MGN[4]和Mixamo[1]。由于我们只对重建训练数据感兴趣，因此在此实验中不使用验证和测试集。由于DeepSDF无法处理开放表面，我们使用[21]生成其地面真值SDF值，该方法使用绕数将复杂的开放表面转换为封闭表面。对于训练和评估，我们对我们的方法使用10作为基于八叉树采样的深度，对DeepSDF使用1024的等效分辨率。为确保类似的采样密度，我们为NDF生成100万个表面点。所有NDF结果（包括以下实验）都使用作者发布的后处理脚本生成，以确保公平比较。

fig.1

图1. 我们展示了由NDF [10]（青色）和我们提出的3PSDF（金色）分别生成的三组形状重建结果。我们的方法能够忠实地重建高保真、复杂的几何细节，包括封闭和开放表面，而NDF则存在网格化问题。每个NDF结果都是从包含100万个点的密集点云重建的，而我们的结果则是使用等效分辨率重建的。

fig.3

图3. 使用不同神经隐式表示的形状重建结果的视觉比较。

table.1

表1. 使用不同神经隐式表示的形状重建的定量比较。

我们在图1和图3中展示了视觉比较，在表1中展示了定量比较。虽然DeepSDF能够重建精细细节，但它无法处理开放表面，如头发、衣物和挡风玻璃。NDF可以处理所有拓扑结构，但存在网格问题——引入了大量自相交和翻转面。我们的方法可以忠实地重建所有复杂的几何体，同时在定量比较中取得最佳性能。

4.3 从点云重建

我们进一步验证3PSDF在从稀疏点云重建形状任务上的表现。遵循NDF[10]，我们首先评估3PSDF在重建封闭表面上的表现，然后展示3PSDF可以表示具有内部结构和开放表面的复杂表面。

fig.4

图4. 在训练时去除内部结构的封闭形状上的点云完成结果比较。

table.2

封闭形状的重建。为了与最先进的方法进行比较：OccNet[26]、IF-Net[9]和DMC[22]，我们在由[43]预处理的ShapeNet汽车类别上进行训练，所有开放表面都被关闭，内部结构被移除。我们在图4和表2中分别展示了使用300和3000个点作为输入的重建结果的定性和定量比较。与其他方法相比，我们的方法可以更好地重建锐利的几何细节，同时在定量测量中优于所有基准方法。

fig.5

图5. 在训练时保留内部结构和开放表面的非封闭形状上的点云完成结果比较。第一行显示第二行重建结果的内部结构。

fig.6

图6. 在MGN和3D-Front数据集上的点云完成性能比较。Chamfer-L2（×10$^{-4}$）比较：MGN：NDF 0.035；我们的方法 - 0.033；3D-Front：NDF - 1.452；我们的方法 - 1.378。

table.2

复杂表面的重建。为了验证3PSDF处理原始、未处理数据的能力，我们训练3PSDF从稀疏点云重建复杂形状，使用三个数据集：ShapeNet[5]中未处理的汽车、MGN[4]中具有开放表面的服装，以及3D-Front[16]中的客厅场景。我们使用NDF[10]和SAL[2]作为重建未处理汽车的基准方法。由于SAL基于传统SDF，我们使用封闭形状作为地面真值。我们在图5和图6中提供了重建结果的视觉比较。SAL难以建模开放表面，例如挡风玻璃和汽车的薄外部结构。NDF可以生成接近目标表面的密集点云。然而，输出点容易聚集（如图6的特写所示），这阻止了BP算法生成高质量的网格结果。相比之下，3PSDF能够忠实地重建内部结构以及开放表面。表2和图6中的定量比较也验证了我们相对于基准方法的优势。

4.4 单视图3D重建

在这个实验中，我们将3PSDF应用于单视图3D重建(SVR)任务，进一步展示其表示能力。我们在MGN数据集[4]和ShapeNet[5]上进行评估。我们使用Chamfer-L2距离和F-score（τ = 体对角线长度的1%）作为评估指标。我们与使用隐式场的代表性SVR方法进行比较，包括IMNet[7]、OccNet[26]和DISN[43]。我们进一步实现了一个基于图像的NDF[10]估计器，但发现仅使用图像特征无法生成合理的结果。由于这两个数据集中的模型通常包含非水密表面，基线方法无法直接处理，我们首先将这些模型转换为水密模型。请注意，我们的表示直接在原始形状上训练，无需这种极其耗时的处理过程。

fig.7

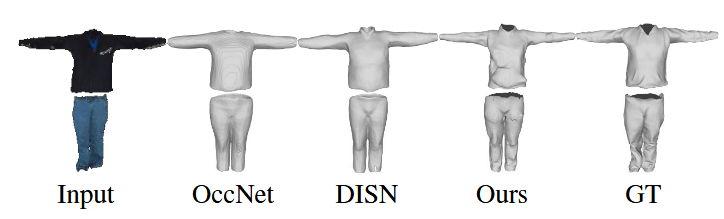
图7. 在MGN数据集上与基于隐式函数的最先进单视图重建方法的定性比较。测试集上的定量评估结果以CD（×10$^{-3}$）和F-score（×10$^{-2}$）指标表示：1.03和69.8（DISN）；1.01和71.0（OccNet）；0.98和71.2（我们的方法）。

MGN上的单视图重建。MGN数据集[4]中的模型表示为具有单层的开放自由形式表面，这对现有的使用隐式函数的单视图重建方法是一个挑战。我们使用每个服装模型的纹理网格渲染RGB图像，并训练一个以图像为条件的网络来预测形状表示。如图7所示，我们的结果捕捉了原始的开放表面结构以及更多的高频几何特征，如褶皱。3PSDF表示在测试集上也取得了最佳的定量结果。

fig.8

图8. 与基于隐式函数的最先进单视图重建方法的定性比较结果。

table.3

表3. 单视图重建的定量比较。Chamfer-L2和F-score分别以×10$^{-3}$和×10$^{-2}$报告。

ShapeNet上的单视图重建。我们使用ShapeNet[5]的一个子集进行评估，从中选择5个类别（飞机、汽车、灯具、椅子、船）共17803个形状。我们使用与Choy等人[12]相同的图像渲染（每个形状24个视图）和训练/测试分割。图8展示了一组定性比较。尽管3PSDF设计用于处理开放表面，但它仍然是一种用于重建ShapeNet中各种3D形状（无论是封闭还是开放表面）的多功能表示。我们不仅忠实地保留了目标形状的原始结构，还捕捉了更多详细的几何体。相反，现有的隐式函数总是依赖于水密形状，这大大限制了它们的表示能力，通常导致过度平滑的几何体、缺乏细节以及不一致的拓扑结构。如表3所示，与现有方法相比，3PSDF取得了最先进的性能，其中5个指标排名第一，其余指标也有可比的结果。

4.5 进一步讨论

fig.9

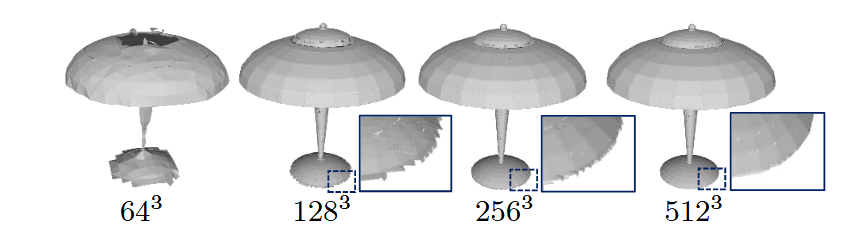
图9. 使用不同分辨率重建形状的结果。从左到右，这些形状的CD（×10$^{-5}$）值分别为：14.49、2.52、2.21和2.12；EMD（×10$^{2}$）值分别为：3.42、0.336、0.267和0.227。

不同分辨率下的重建精度/外观。由于3PSDF在3D空间中连续定义，它可以使用任意分辨率表示形状。图9给出了从粗到细的形状近似结果，我们离散化体积空间并使用不同的网格分辨率来表示3D形状。实验结果表明，随着分辨率的增加，3PSDF的近似质量提高，导致更平滑的形状边界和更高的重建精度。

场到网格转换的时间成本。我们定量评估了不同输出采样密度下场到网格转换的时间成本。对于八叉树深度为6（$64^3$）、7（$128^3$）、8（$256^3$）和9（$512^3$），3PSDF单个形状的平均场到网格转换时间分别为0.006秒、0.11秒、0.54秒和3.72秒。相比之下，给定可比数量的采样点，NDF[10]的转换时间为：2.1秒、15分钟、3小时、34小时，使用NDF提供的后处理设置（半径=0.005）。实验在配备48核AMD EPYC CPU和64GB内存的机器上进行。

table.4

表4. 使用不同采样策略的重建精度。

不同的采样策略。我们进一步研究了不同采样策略对3PSDF性能的影响；我们在未处理的汽车数据上评估从点云重建形状的任务。使用三种策略生成采样点：1）在空间中随机抽取样本；2）均匀采样，以相等距离生成相邻点；3）基于八叉树的采样，使用叶八叉树单元的角点作为训练样本。我们对所有策略使用约1800万个采样点。表4显示，基于八叉树的采样产生最佳结果。与其他方法相比，基于八叉树的采样能够密集地采样具有内部/外部标签的点，生成包含所有3个标签的更平衡的训练集。除非另有说明，否则我们对所有实验使用基于八叉树的采样。

局限性。3PSDF在重建非常接近的多层表面时存在困难，特别是当分辨率较低时。这是因为与SDF相比，3PSDF需要更密集的采样率，以便在中间插入空层以防止伪影表面。此外，鉴于3PSDF增强的表示能力，它需要更多信息丰富的特征来学习和更长的训练时间；例如，与单一图像相比，给定点云作为输入时，网络收敛得更快并实现更好的几何形状。

5 结论和讨论

我们引入了3PSDF，一种可学习的隐式距离函数，用于表示具有任意拓扑结构的3D形状。与广泛使用的只能编码水密形状的隐式表示（如SDF）不同，3PSDF可以忠实地表示具有开放和封闭表面的各种形状。3PSDF的关键见解是引入NULL符号来额外指示表面的不存在。我们进一步制定了基于分类的学习范式，以有效地学习这种表示。因此，距离函数的表示能力显著增强。广泛的评估表明，3PSDF是一种适用于各种3D重建任务的多功能隐式表示。

未来工作。我们在补充材料中展示了3PSDF可以通过结合二元分类和回归的替代方法学习。与3路分类相比，这种方法有可能在训练时使用更少的采样点生成更平滑的表面。然而，它不如3路方法稳健，因为它需要两个分支的结果很好地对齐，以防止孔洞和伪影。研究如何解决这个问题将是一个有趣的未来方向。

评论