k054 Equivariance, The Lie Derivative for Measuring Learned Equivariance

Zhangwenniu 于 2025-03-14 发布  |   阅读量: 次

论文链接

Arxiv link

2023 ICLR Link

发表时间（Arxiv）： [v1] Thu, 6 Oct 2022 15:20:55 UTC (2,187 KB) [v2] Tue, 18 Jun 2024 15:01:13 UTC (2,199 KB)

论文重点与难点

1 研究背景与动机

2 Lie导数与局部等变性误差（LEE）

\[L_Y(f) = \lim_{t \to 0} \frac{1}{t} [\rho_2(g)^{-1} f(\rho_1(g)x) - f(x)]\]

其中$g = \Phi_t^Y$是沿向量场$Y$的流。

\[\text{LEE}(f) = \mathbb{E}_{x \sim D} \|L_X f(x)\|^2 / \dim(V_2)\]

LEE的一个重要特性是它可以自然地分解到神经网络的每一层，从而允许对每一层的等变性贡献进行分析。

3 等变性误差的来源

\[L_X(NN) = \sum_{i=1}^N df_{N:i+1} L_X f_i\]

这种分解揭示了每一层对整体等变性误差的贡献，尤其是非线性层和下采样层的显著贡献。

4 实验结果与发现

5 难点与挑战

6 结论与展望

论文详细讲解

THE LIE DERIVATIVE FOR MEASURING LEARNED EQUIVARIANCE

1 研究背景与动机

等变性（Equivariance）是机器学习模型中一个重要的性质，它确保模型的输出能够与输入的对称性保持一致。例如，当图像发生平移或旋转时，等变模型的输出也会相应地平移或旋转。卷积神经网络（CNN）的成功部分归功于其对平移等变性的天然编码。然而，Vision Transformer（ViT）等非卷积架构在没有明确等变性偏置的情况下，也能取得与CNN相当甚至更好的性能。这表明，数据增强和训练方法可能在模型的等变性中也起到了关键作用。因此，本文旨在通过Lie导数这一工具，系统地研究不同架构模型的等变性，并揭示架构设计、训练方法等因素对等变性的影响。

2 Lie导数与局部等变性误差（LEE）

Lie导数是一种用于量化函数在连续变换下对称性保持程度的数学工具。它通过计算函数在无穷小变换下的变化率来衡量等变性误差。具体来说，对于一个函数$f: V_1 \to V_2$和一个连续对称群$G$，Lie导数$L_Y(f)$定义为：

\[L_Y(f) = \lim_{t \to 0} \frac{1}{t} [\rho_2(g)^{-1} f(\rho_1(g)x) - f(x)]\]

其中，$g = \Phi_t^Y$是沿向量场$Y$的流，$\rho_1$和$\rho_2$分别是输入和输出空间的群表示。

局部等变性误差（LEE）是Lie导数在模型输出上的平均值，用于量化模型的整体等变性误差：

\[\text{LEE}(f) = \mathbb{E}_{x \sim D} \|L_X f(x)\|^2 / \dim(V_2)\]

LEE的一个重要特性是它可以自然地分解到神经网络的每一层，从而允许对每一层的等变性贡献进行分析。这种分解基于Lie导数的链式法则：

\[L_X(f \circ h)(x) = (L_X f)(h(x)) + df_{h(x)}(L_X h)(x)\]

其中，$df_{h(x)}$是函数$f$在$h(x)$处的Jacobian矩阵。通过这种分解，可以分析每一层对整体等变性误差的贡献。

3 等变性误差的来源

论文指出，空间混叠（Aliasing）是导致等变性误差的主要原因。混叠是指由于采样频率有限，高频成分被错误地映射为低频成分的现象。在神经网络中，混叠现象尤其常见，尤其是在卷积网络中的下采样层和非线性激活函数（如ReLU）中。例如，非线性激活函数会引入新的高频成分，这些成分可能超出采样频率的限制，从而导致混叠。

论文通过理论分析和实验验证，揭示了混叠对等变性的影响。具体来说，混叠会破坏连续变换（如平移和旋转）的等变性。例如，当一个连续图像被平移时，其傅里叶分量会获得一个相位偏移。然而，当图像被混叠时，这种相位偏移会被错误地缩放，导致平移量不正确。

4 实验设计与结果

论文对大量预训练的图像分类模型进行了分析，涵盖了CNN、ViT和Mixer架构。实验结果揭示了以下关键发现：

1. 不同架构的等变性对比

尽管CNN在设计上更注重平移等变性，但在实际性能上，ViT和Mixer在训练后往往能更好地捕捉等变性。这表明，等变性不仅依赖于架构设计，还与训练数据和增强方法密切相关。

2. 模型规模与等变性的关系

实验表明，模型规模的增加、数据量的扩大以及训练方法的改进，都能显著降低等变性误差，甚至超过通过架构设计（如Blur-Pool）所能达到的效果。例如，通过改进训练方法（如Mixup和CutMix）或使用半监督学习，可以显著降低等变性误差。

3. 泛化与等变性的关系

论文发现，模型在训练数据上的等变性与测试数据上的等变性存在差距，尤其是在分布外（OOD）数据上。此外，尽管CNN在设计上更注重平移等变性，但在实际性能上，ViT和Mixer在训练后往往能更好地捕捉等变性。

5 关键结论

1. Lie导数的有效性

Lie导数提供了一个统一的等变性测量框架，能够对不同架构的模型进行公平的比较。它不仅能够量化模型的整体等变性误差，还能分解到每一层，揭示每一层对等变性误差的贡献。

2. 架构与训练的权衡

尽管架构设计（如CNN的平移等变性）对模型性能有一定影响，但训练方法、数据量和模型规模对等变性的影响更为显著。这表明，在实际应用中，可以通过改进训练方法和扩大数据量来提升模型的等变性，而不必依赖于复杂的架构设计。

3. 等变性与泛化的联系

等变性与模型的泛化能力密切相关。实验表明，具有更强等变性的模型往往在测试数据上表现更好。然而，模型在训练数据上的等变性与测试数据上的等变性存在差距，尤其是在分布外数据上。这表明，尽管模型可以通过数据增强学习到较强的等变性，但在未见过的对称性上，等变性仍然不足。

4. 混叠的影响

混叠是导致等变性误差的主要原因。论文通过理论分析和实验验证，揭示了混叠对等变性的影响。混叠不仅影响卷积网络，还影响非卷积架构（如ViT和Mixer）。因此，如何在模型设计中减少混叠的影响，是提升等变性的关键。

6 未来研究方向

1. 减少混叠的影响

如何在模型设计中减少混叠的影响，是提升等变性的关键。例如，可以探索更平滑的非线性激活函数或改进的下采样方法，以减少混叠现象。

2. 提升分布外数据的等变性

尽管模型可以通过数据增强学习到较强的等变性，但在分布外数据上，等变性仍然不足。因此，需要探索新的方法来提升模型在未见过的对称性上的等变性。

3. 架构与训练方法的结合

本文表明，架构设计和训练方法对等变性的影响相当。未来的研究可以探索如何结合架构设计和训练方法，以进一步提升模型的等变性和泛化能力。

4. 更广泛的对称性研究

本文主要研究了平移、旋转和缩放等常见对称性。未来可以探索更广泛的对称性（如高阶对称性或非线性对称性），以进一步提升模型的泛化能力。

通过Lie导数这一工具，本文系统地研究了不同架构模型的等变性，并揭示了架构设计、训练方法等因素对等变性的影响。这些发现为未来的研究提供了新的方向，也为设计更强大的视觉模型提供了理论支持。

论文方法部分详细讲解

1 Lie导数与局部等变性误差（LEE）

为了量化模型的等变性，论文引入了Lie导数这一数学工具。Lie导数能够衡量函数在连续对称变换下的变化率，从而用于评估等变性误差。具体而言，Lie导数的定义如下：

假设函数$f: V_1 \to V_2$，对称群$G$的元素$g$通过表示$\rho_1$作用于输入空间$V_1$，通过表示$\rho_2$作用于输出空间$V_2$。Lie导数$L_Y(f)$沿着向量场$Y$定义为：

\[L_Y(f) = \lim_{t \to 0} \frac{1}{t} \left[ \rho_2(g)^{-1} f(\rho_1(g)x) - f(x) \right]\]

其中，$g = \Phi_t^Y$是沿向量场$Y$的流。

局部等变性误差（LEE）是Lie导数在数据分布上的期望值，用于量化模型的整体等变性误差：

\[\text{LEE}(f) = \mathbb{E}_{x \sim D} \left[ \|L_X f(x)\|^2 / \dim(V_2) \right]\]

2 Lie导数的链式法则与层间分解

Lie导数的一个关键特性是它满足链式法则，这使得它可以自然地分解到神经网络的每一层。假设网络由多个函数复合而成，即$NN(x) = f_N \circ f_{N-1} \circ \cdots \circ f_1(x)$，则Lie导数可以分解为：

\[L_X(NN) = \sum_{i=1}^N df_{N:i+1} L_X f_i\]

其中，$df_{N:i+1}$表示从第$i$层到输出层的Jacobian矩阵。通过这种方式，可以量化每一层对整体等变性误差的贡献。

3 Lie导数的计算

论文中展示了如何使用自动微分工具（如PyTorch）计算Lie导数。以旋转为例，Lie导数的计算可以表示为：

def rotation_lie_deriv(model, imgs):
    def rotated_model(theta):
        z = model(rotate(imgs, theta))
        img_like = (len(z.shape) == 4)
        return rotate(z, -theta) if img_like else z
    return jvp(rotated_model, torch.zeros(1, requires_grad=True))[-1]

其中，rotate函数用于对图像进行旋转，jvp是PyTorch中的Jacobian-vector product操作，用于计算导数。

4 层间等变性误差的分析

通过Lie导数的层间分解，可以分析每一层对等变性误差的贡献。论文中展示了不同架构（CNN、ViT、Mixer）的层间等变性误差分布：

这种分析揭示了混叠现象在不同层中的影响，尤其是非线性层如何引入高频成分，从而导致等变性误差。

5 与现有等变性度量方法的对比

论文还对比了Lie导数与其他等变性度量方法（如整像素平移一致性、分数像素平移一致性）的优缺点。Lie导数的主要优势包括：

6 大规模模型分析

论文通过分析大量预训练模型（包括CNN、ViT、Mixer等架构），验证了Lie导数在不同模型中的适用性。实验表明，模型的等变性与测试精度呈正相关，且模型规模、数据量和训练方法对等变性的影响大于架构设计。

总结

论文通过引入Lie导数，提供了一个统一的框架来量化和分析神经网络的等变性。Lie导数不仅能够衡量模型的整体等变性误差，还能通过层间分解揭示每一层对等变性的影响。这种方法为理解模型的对称性学习提供了新的视角，并为改进模型设计和训练方法提供了理论支持。

fig.1

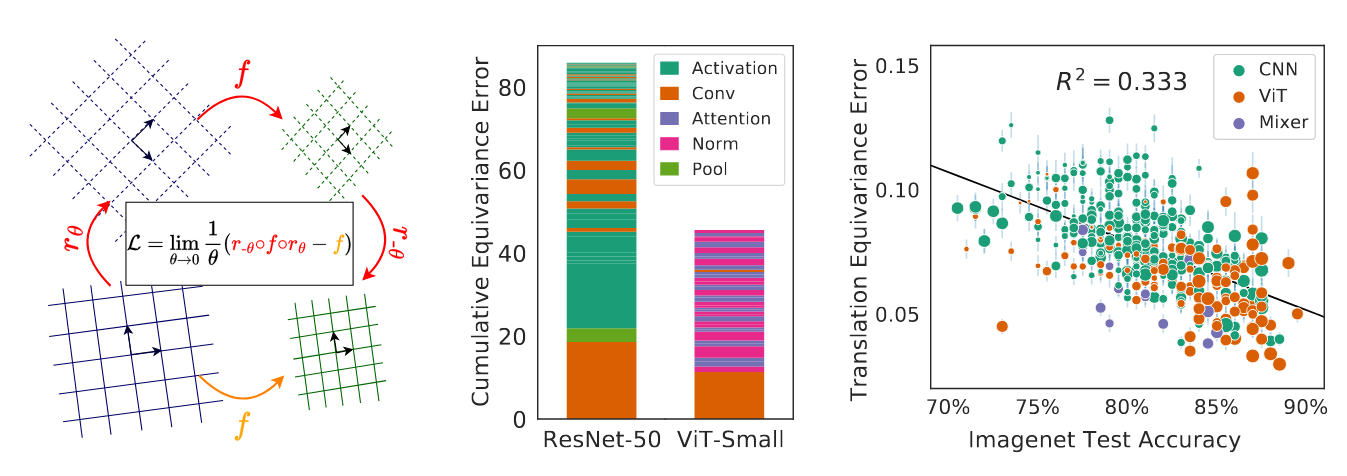
图1：（左）：李导数衡量函数在连续变换（如旋转）下的等变性。（中）：利用李导数，我们量化了每一层对模型等变误差的贡献。分析表明，非线性操作对等变误差的贡献出乎意料地大，这影响了CNN和ViT架构。（右）：通过李导数测量的平移等变性与分类模型的泛化能力相关，涵盖了卷积和非卷积架构。尽管CNN因其固有的平移等变性而闻名，但ViT和Mixer模型在训练后通常比CNN模型更具平移等变性。

fig.2

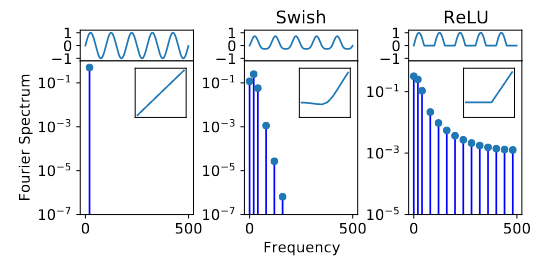
图2：非线性操作会生成新的高频谐波。

fig.3

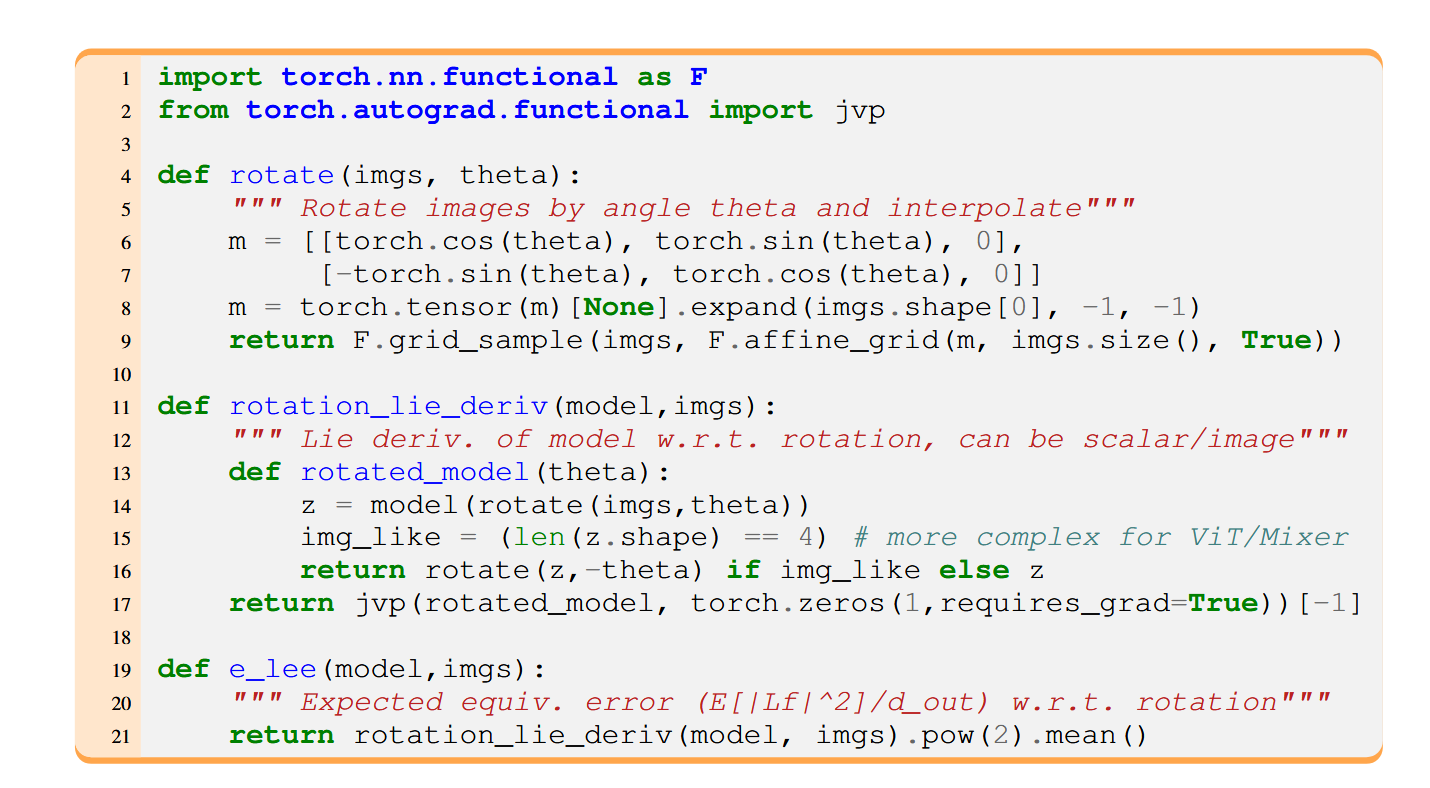
图3：李导数可以通过自动微分计算。我们展示了如何在PyTorch中实现连续旋转的李导数（Paszke等，2019）。实验中的实现略有不同，以提高计算效率，并通过grid_sample传递二阶梯度。

fig.4

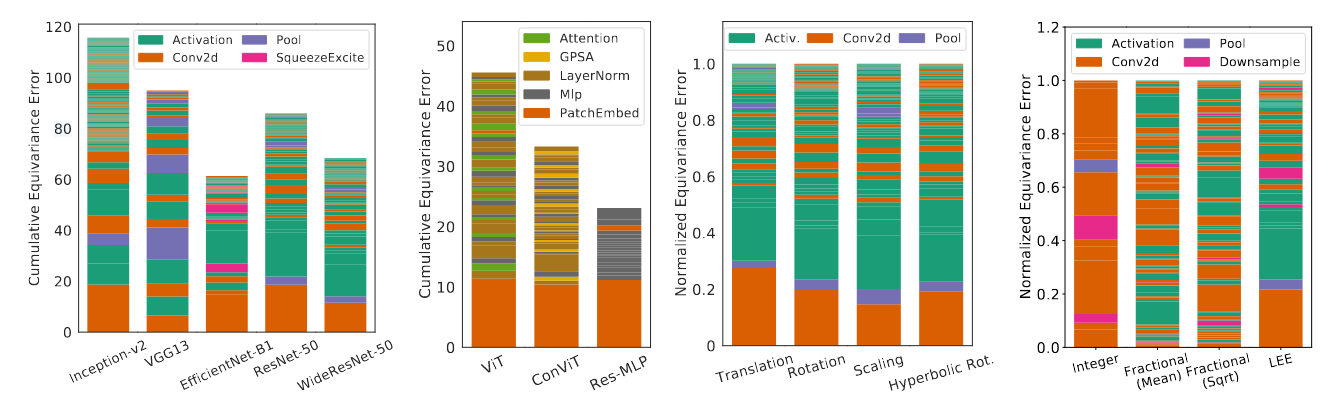
图4：按层顺序累积显示的等变性贡献。左：卷积架构。在所有CNN中，等变误差主要来自下采样和非线性操作。中左：非卷积架构。初始的patch嵌入（一种步幅卷积）是ViT和Mixer的最大贡献者。其余误差均匀分布在其他非线性操作中。中右：ResNet-50在不同变换下的等变误差百分比。尽管ResNet-50是为平移等变性设计的，但每一层对其他仿射变换的等变误差贡献几乎相同，表明混叠是等变误差的主要来源。右：将LEE与其他平移等变性指标进行比较。使用整数平移会忽略等变误差的关键贡献者（如激活函数），而使用分数平移则可能因归一化选择（$N$或$\sqrt{N}$）导致截然不同的结果。LEE捕捉了混叠效应，且设计决策最少。

fig.5

fig.1

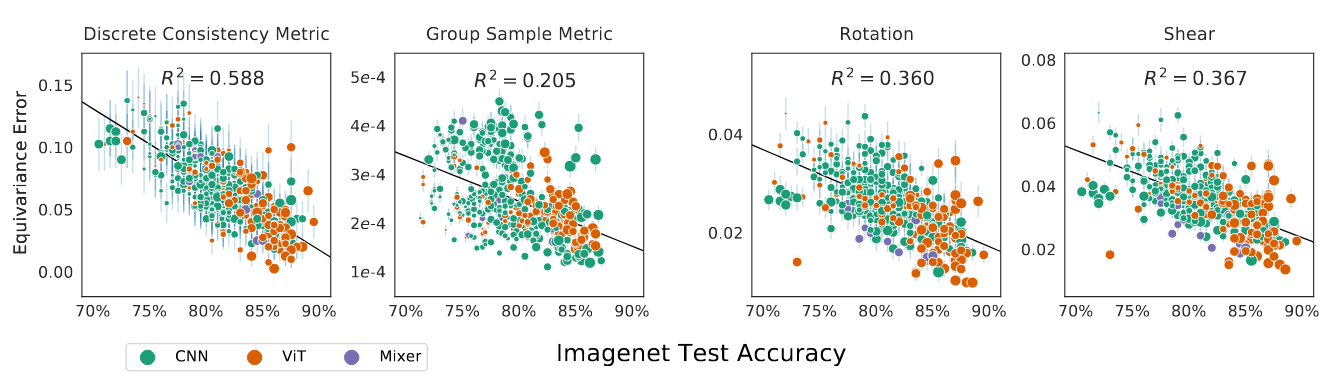
图5：在ImageNet测试集上评估的等变性指标。左：非LEE等变性指标与图1中的趋势相似，尽管使用了更大的多像素变换。右：旋转和剪切李导数的范数。在所有架构中，泛化能力强的模型对许多常见仿射变换的等变性更强。标记大小表示模型大小。误差条显示了在等变性计算中使用的测试集图像的一个标准误差。

fig.6

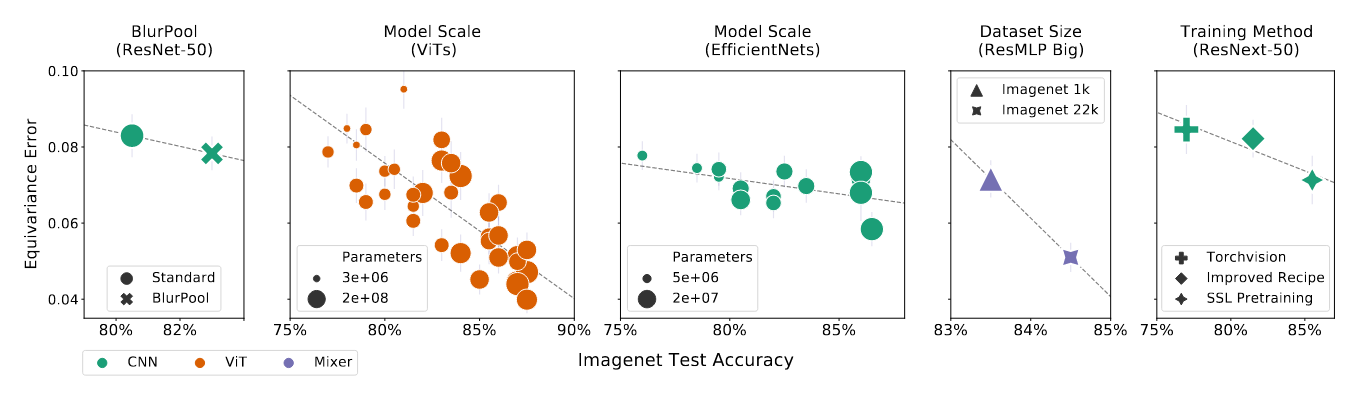
图6：减少平移等变误差的案例研究，从左到右编号。1：Blur-Pool（Zhang，2019）是一种改进等变性的架构变化，减少了等变误差，但效果不如改进训练方案或增加模型或数据集的规模。2-3：增加固定模型族（这里为ViT（El-Nouby等，2021）和EfficientNet（Tan & Le，2019a））的参数数量。4：增加ResMLP Big（Touvron等，2021a）模型的训练数据集规模。5：通过改进数据增强（Wightman等，2021）或SSL预训练（Yalniz等，2019）改变ResNeXt-50（Xie等，2017）的训练方案。误差条显示了李导数计算中图像的一个标准误差。

fig.7

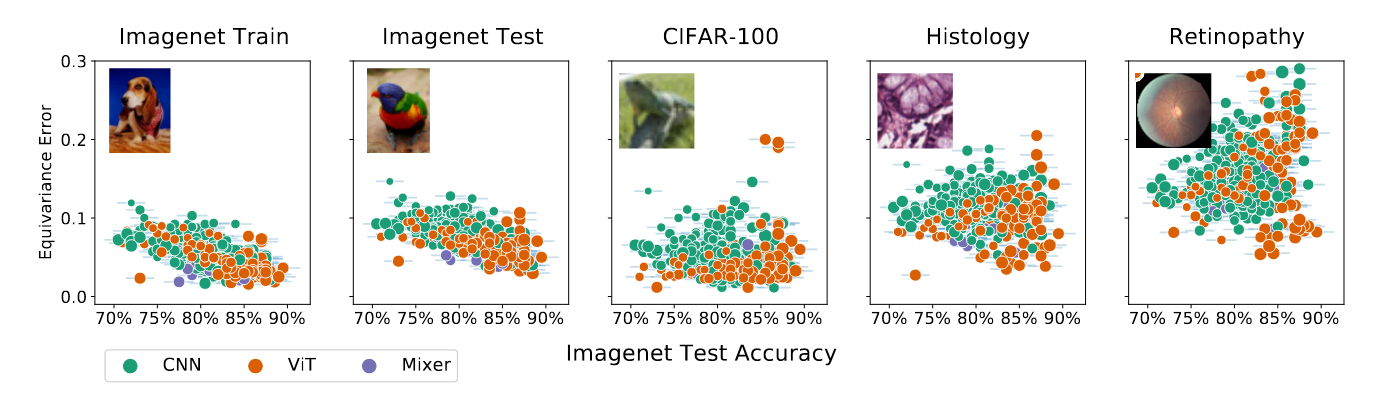
图7：模型在测试数据上的等变性较差，并且随着数据远离训练流形而逐渐降低等变性。作为具有相似分布的数据示例，我们展示了ImageNet训练集和测试集以及CIFAR-100上的等变误差。作为分布外数据的示例，我们使用了两个医学数据集（通常使用ImageNet预训练），一个用于组织学（Kather等，2016），另一个用于视网膜病变（Kaggle & EyePacs，2015）。

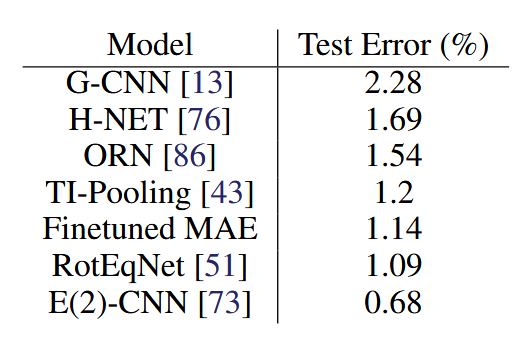
table.1

表1：我们在RotMNIST上微调的MAE与几种明确设计为编码旋转不变性的架构具有竞争力，而旋转不变性显然对泛化至关重要。

评论