论文重点与难点

1 研究背景与动机

• 背景：自2017年Transformer模型提出以来，其在序列建模任务中取得了巨大成功，但其计算复杂度随序列长度二次增长，限制了其在长序列任务中的应用。因此，研究者重新关注可并行化的新型递归模型（RNN），这些模型在训练时可并行计算，性能与Transformer相当，且更易于扩展。

• 动机：论文重新审视了在Transformer出现之前主导序列建模领域的传统RNN模型（如LSTM和GRU），通过简化这些模型，提出了最小化版本（minLSTM和minGRU），旨在减少参数量、实现训练时的完全并行化，并在多种任务上验证其性能。

2 研究方法

• 简化传统RNN模型：

  • minGRU：

    1. 去除对前一状态的依赖：将GRU的更新门和候选隐藏状态的计算公式从依赖于前一隐藏状态 \(h_{t-1}\) 改为仅依赖于当前输入 \(x_t\)，从而去除递归依赖，使其可并行计算。

    2. 去除候选隐藏状态的范围限制：去掉 \(\tanh\) 函数，进一步简化模型。

    3. 最终得到的minGRU公式为：

\[\begin{aligned} z_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ \tilde{h}_t &= \text{Linear}_{dh}(x_t) \\ h_t &= (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t \end{aligned}\]

• minLSTM：

  1. 去除对前一状态的依赖：类似GRU，将LSTM的遗忘门、输入门和候选细胞状态的计算公式改为仅依赖于当前输入 \(x_t\)。

  2. 去除范围限制：去掉细胞状态和隐藏状态的 \(\tanh\) 函数。

  3. 简化输出缩放：去掉输出门，直接将细胞状态作为隐藏状态输出。

  4. 最终得到的minLSTM公式为：

\[\begin{aligned} f_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ i_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ \tilde{h}_t &= \text{Linear}_{dh}(x_t) \\ h_t &= f_t \odot h_{t-1} + i_t \odot \tilde{h}_t \end{aligned}\]

• 并行化训练：通过去除对前一状态的依赖，minLSTM和minGRU可以利用并行前缀扫描算法（Parallel Scan）进行训练，避免了传统RNN的逐时间步反向传播（BPTT），显著提高了训练效率。

3 实验设计与结果

• 实验设计：

  • 任务选择：包括选择性复制任务（Selective Copying Task）、强化学习任务（MuJoCo控制任务）、语言建模任务（Shakespeare数据集）等，覆盖了序列建模的多个领域。

  • 对比模型：与传统RNN（LSTM和GRU）、Transformer以及最新提出的并行化递归模型（如Mamba）进行对比。

• 实验结果：

  • 训练效率：minLSTM和minGRU在训练时的运行时间显著优于传统RNN，且随着序列长度增加，加速比更高。例如，在序列长度为4096时，minGRU和minLSTM比传统GRU和LSTM快约1324倍和1361倍。

  • 性能表现：

    • 在选择性复制任务中，minGRU和minLSTM能够成功解决任务，性能与Mamba的S6模型相当，优于其他现代基线模型（如S4和Hyena）。

    • 在强化学习任务中，minLSTM和minGRU在多个环境中的表现优于Decision S4，与Decision Transformer、Aaren和Mamba相当。

    • 在语言建模任务中，minGRU和minLSTM的测试损失与Mamba和Transformer相当，但训练速度更快。Transformer需要约2.5倍的训练步数才能达到类似的性能。

4 难点与解决方案

• 难点：

  1. 去除对前一状态的依赖：传统RNN的门控机制依赖于前一状态，这使得模型难以并行化训练。论文通过简化模型结构，将门控机制的输入改为仅依赖于当前输入，从而解决了这一问题。

  2. 模型性能的保持：在简化模型结构后，如何保持甚至提升模型性能是一个关键挑战。论文通过实验验证了minLSTM和minGRU在多种任务上的有效性，证明了简化模型的性能与现代复杂模型相当。

  3. 数值稳定性：在并行化训练中，数值稳定性是一个重要问题。论文通过引入对数空间实现（Log-Space Implementation）来提高数值稳定性。

• 解决方案：

  • 并行化训练：通过并行前缀扫描算法，minLSTM和minGRU能够实现训练时的完全并行化，显著提高了训练效率。

  • 多层堆叠：虽然单层minLSTM和minGRU的门控机制是时间无关的，但通过堆叠多层，模型能够学习到更复杂的函数，从而提升性能。

  • 对数空间实现：为了提高数值稳定性，论文提出了对数空间版本的minLSTM和minGRU，通过在对数空间中计算并行扫描，避免了数值溢出等问题。

5 结论与展望

• 结论：论文证明了通过简化传统RNN模型（LSTM和GRU），可以得到具有更少参数、完全并行化训练能力且性能与现代复杂模型相当的最小化版本（minLSTM和minGRU）。这些模型在多种任务上表现出色，挑战了当前社区对复杂架构的偏好。

• 展望：论文提出了一个值得深思的问题——“RNN是否已经足够？”尽管现代复杂模型在某些任务上取得了显著进展，但传统RNN模型的简化版本在效率和性能上仍具有竞争力。未来的研究可以进一步探索传统模型的潜力，以及如何在复杂性和效率之间找到更好的平衡。

论文详细解读

1. 研究背景

自1990年代以来，循环神经网络（RNN）及其变体（如LSTM和GRU）一直是序列建模的核心方法。然而，由于其固有的顺序性，传统RNN在训练长序列时效率低下。2017年，Transformer模型的出现凭借其并行化训练机制彻底改变了深度学习领域，但在处理长序列时，其二次复杂度的计算成本仍然较高。因此，研究者们重新关注可并行化训练且能有效扩展的新型递归模型。

2. 研究目标

本文旨在重新审视传统RNN模型（LSTM和GRU），通过简化这些模型，提出新的最小化版本（minLSTM和minGRU），使其在训练时完全可并行化，同时减少参数量，并在多种任务上验证其性能是否能够与现代复杂模型相媲美。

3. 研究方法

3.1 传统RNN模型回顾

• LSTM：通过引入细胞状态和多个门控机制（输入门、遗忘门、输出门）来解决梯度消失问题，能够有效捕捉长期依赖关系。LSTM的计算公式为：

\[\begin{aligned} f_t &= \sigma(\text{Linear}_{dh}([x_t, h_{t-1}])) \\ i_t &= \sigma(\text{Linear}_{dh}([x_t, h_{t-1}])) \\ \tilde{c}_t &= \tanh(\text{Linear}_{dh}([x_t, h_{t-1}])) \\ c_t &= f_t \odot c_{t-1} + i_t \odot \tilde{c}_t \\ o_t &= \sigma(\text{Linear}_{dh}([x_t, h_{t-1}])) \\ h_t &= o_t \odot \tanh(c_t) \end{aligned}\]

其中，\(h_t\) 是隐藏状态，\(c_t\) 是细胞状态，\(dh\) 是隐藏状态的维度。

• GRU：通过简化LSTM的结构，引入更新门和重置门，减少了参数量并提高了训练速度。GRU的计算公式为：

\[\begin{aligned} z_t &= \sigma(\text{Linear}_{dh}([x_t, h_{t-1}])) \\ r_t &= \sigma(\text{Linear}_{dh}([x_t, h_{t-1}])) \\ \tilde{h}_t &= \tanh(\text{Linear}_{dh}([x_t, r_t \odot h_{t-1}])) \\ h_t &= (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t \end{aligned}\]

3.2 提出的最小化版本（minLSTM和minGRU）

• minGRU：

  1. 去除对前一状态的依赖：将GRU的更新门和候选隐藏状态的计算公式从依赖于\(h_{t-1}\)改为仅依赖于当前输入\(x_t\)，从而去除递归依赖，使其可并行计算。

\[\begin{aligned} z_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ \tilde{h}_t &= \tanh(\text{Linear}_{dh}(x_t)) \end{aligned}\]

1. 去除候选隐藏状态的范围限制：去掉\(\tanh\)函数，进一步简化模型。

\[\tilde{h}_t = \text{Linear}_{dh}(x_t)\]

1. 最终得到的minGRU公式为：

\[\begin{aligned} z_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ \tilde{h}_t &= \text{Linear}_{dh}(x_t) \\ h_t &= (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t \end{aligned}\]

• minLSTM：

  1. 去除对前一状态的依赖：类似GRU，将LSTM的遗忘门、输入门和候选细胞状态的计算公式改为仅依赖于当前输入\(x_t\)。

\[\begin{aligned} f_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ i_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ \tilde{c}_t &= \tanh(\text{Linear}_{dh}(x_t)) \end{aligned}\]

1. 去除范围限制：去掉细胞状态和隐藏状态的\(\tanh\)函数。

\[\tilde{c}_t = \text{Linear}_{dh}(x_t)\]

1. 简化输出缩放：去掉输出门，直接将细胞状态作为隐藏状态输出。

\[h_t = c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t\]

1. 最终得到的minLSTM公式为：

\[\begin{aligned} f_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ i_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ \tilde{h}_t &= \text{Linear}_{dh}(x_t) \\ h_t &= f_t \odot h_{t-1} + i_t \odot \tilde{h}_t \end{aligned}\]

4. 实验设计与结果

4.1 实验设置

• 任务选择：

  • 选择性复制任务（Selective Copying Task）：模型需要从序列中提取数据标记，同时忽略噪声标记。

  • 强化学习任务（MuJoCo控制任务）：包括HalfCheetah、Hopper和Walker环境，评估模型在不同数据质量下的表现。

  • 语言建模任务（Shakespeare数据集）：基于莎士比亚作品的字符级语言建模任务，评估模型的生成能力。

• 对比模型：

  • 传统RNN（LSTM和GRU）

  • Transformer

  • 现代递归模型（如Mamba）

4.2 实验结果

• 训练效率：

  • minLSTM和minGRU在训练时的运行时间显著优于传统RNN。例如，在序列长度为4096时，minGRU和minLSTM比传统GRU和LSTM快约1324倍和1361倍。

  • minLSTM和minGRU的训练速度与Mamba相当，但比Transformer更快。Transformer需要约2.5倍的训练步数才能达到类似的性能。

• 性能表现：

  • 选择性复制任务：minGRU和minLSTM能够成功解决任务，性能与Mamba的S6模型相当，优于其他现代基线模型（如S4和Hyena）。

  • 强化学习任务：minLSTM和minGRU在多个环境中的表现优于Decision S4，与Decision Transformer、Aaren和Mamba相当。

  • 语言建模任务：minGRU和minLSTM的测试损失与Mamba和Transformer相当，但训练速度更快。

5. 关键结论

• 通过简化传统RNN模型（LSTM和GRU），可以得到具有更少参数、完全并行化训练能力且性能与现代复杂模型相当的最小化版本（minLSTM和minGRU）。

• 这些最小化版本在多种任务上表现出色，挑战了当前社区对复杂架构的偏好，提出了“RNN是否已经足够？”的问题。

6. 局限性

• 实验受限于硬件条件，使用了较旧的GPU（如P100、T4），导致训练时需要使用梯度累积，降低了训练效率。

• 尽管如此，实验结果表明，minLSTM和minGRU在效率和性能上的优势可能在更大规模的设置中仍然成立。

7. 未来工作

• 进一步探索传统RNN模型的潜力，研究如何在复杂性和效率之间找到更好的平衡。

• 在更大规模的数据集和更复杂的任务上验证minLSTM和minGRU的性能。

• 探索如何将这些最小化版本与其他现代技术（如稀疏注意力、低秩近似）结合，以进一步提升模型的性能和效率。

论文方法部分详细讲解

1. 传统RNN模型回顾

论文首先回顾了两种经典的RNN模型：LSTM和GRU，它们是序列建模领域的基石。

• LSTM（长短期记忆网络）：

  LSTM通过引入细胞状态（cell state）和多个门控机制来解决传统RNN的梯度消失问题。其核心公式为：

\[\begin{aligned} f_t &= \sigma(\text{Linear}_{dh}([x_t, h_{t-1}])) \quad \text{(遗忘门)} \\ i_t &= \sigma(\text{Linear}_{dh}([x_t, h_{t-1}])) \quad \text{(输入门)} \\ \tilde{c}_t &= \tanh(\text{Linear}_{dh}([x_t, h_{t-1}])) \quad \text{(候选细胞状态)} \\ c_t &= f_t \odot c_{t-1} + i_t \odot \tilde{c}_t \quad \text{(细胞状态更新)} \\ o_t &= \sigma(\text{Linear}_{dh}([x_t, h_{t-1}])) \quad \text{(输出门)} \\ h_t &= o_t \odot \tanh(c_t) \quad \text{(隐藏状态)} \end{aligned}\]

LSTM包含四个主要部分：遗忘门、输入门、候选细胞状态和输出门。这些门控机制使得LSTM能够有效地捕捉长期依赖关系。

• GRU（门控循环单元）：

  GRU是对LSTM的简化，通过引入更新门和重置门来减少参数量并提高训练速度。其核心公式为：

\[\begin{aligned} z_t &= \sigma(\text{Linear}_{dh}([x_t, h_{t-1}])) \quad \text{(更新门)} \\ r_t &= \sigma(\text{Linear}_{dh}([x_t, h_{t-1}])) \quad \text{(重置门)} \\ \tilde{h}_t &= \tanh(\text{Linear}_{dh}([x_t, r_t \odot h_{t-1}])) \quad \text{(候选隐藏状态)} \\ h_t &= (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t \quad \text{(隐藏状态更新)} \end{aligned}\]

GRU将LSTM的遗忘门和输入门合并为更新门，同时引入重置门来控制前一隐藏状态的影响。

2. 提出的最小化版本（minLSTM和minGRU）

2.1 minGRU：最小化的GRU

论文通过以下步骤将GRU简化为minGRU，使其能够并行化训练：

• Step 1：去除对前一状态的依赖

  传统GRU的更新门和候选隐藏状态依赖于前一隐藏状态 \(h_{t-1}\)。为了实现并行化，论文去除了这种依赖，仅保留对当前输入 \(x_t\) 的依赖：

\[\begin{aligned} z_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ \tilde{h}_t &= \tanh(\text{Linear}_{dh}(x_t)) \end{aligned}\]

这样，所有时间步的 \(z_t\) 和 \(\tilde{h}_t\) 可以并行计算。

• Step 2：去除候选隐藏状态的范围限制

  为了进一步简化模型，论文去除了 \(\tanh\) 函数，使得候选隐藏状态 \(\tilde{h}_t\) 的范围不再受限：

\[\tilde{h}_t = \text{Linear}_{dh}(x_t)\]

这一步减少了模型的非线性，但提高了计算效率。

• 最终的minGRU公式：

\[\begin{aligned} z_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ \tilde{h}_t &= \text{Linear}_{dh}(x_t) \\ h_t &= (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t \end{aligned}\]

minGRU通过去除对前一状态的依赖和范围限制，实现了训练时的完全并行化，同时显著减少了参数量。

2.2 minLSTM：最小化的LSTM

论文通过以下步骤将LSTM简化为minLSTM，使其能够并行化训练：

• Step 1：去除对前一状态的依赖

  传统LSTM的遗忘门、输入门和候选细胞状态依赖于前一隐藏状态 \(h_{t-1}\)。为了实现并行化，论文去除了这种依赖，仅保留对当前输入 \(x_t\) 的依赖：

\[\begin{aligned} f_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ i_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ \tilde{c}_t &= \tanh(\text{Linear}_{dh}(x_t)) \end{aligned}\]

这样，所有时间步的 \(f_t\)、\(i_t\) 和 \(\tilde{c}_t\) 可以并行计算。

• Step 2：去除范围限制

  为了进一步简化模型，论文去除了 \(\tanh\) 函数，使得候选细胞状态 \(\tilde{c}_t\) 的范围不再受限：

\[\tilde{c}_t = \text{Linear}_{dh}(x_t)\]

• Step 3：简化输出缩放

  传统LSTM通过输出门 \(o_t\) 来控制隐藏状态的输出。为了简化模型，论文去除了输出门，直接将细胞状态作为隐藏状态输出：

\[h_t = c_t = f_t \odot h_{t-1} + i_t \odot \tilde{c}_t\]

这一步减少了模型的复杂性，同时保持了LSTM的核心特性。

• 最终的minLSTM公式：

\[\begin{aligned} f_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ i_t &= \sigma(\text{Linear}_{dh}(x_t)) \\ \tilde{h}_t &= \text{Linear}_{dh}(x_t) \\ h_t &= f_t \odot h_{t-1} + i_t \odot \tilde{h}_t \end{aligned}\]

minLSTM通过去除对前一状态的依赖、范围限制和输出门，实现了训练时的完全并行化，同时显著减少了参数量。

3. 并行化训练

为了实现并行化训练，论文利用了并行前缀扫描算法（Parallel Scan）。该算法可以高效地计算形如 \(v_t = a_t \odot v_{t-1} + b_t\) 的递归关系。具体来说：

• 对于minGRU，递归关系可以表示为：

\[h_t = (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t\]

其中，\(a_t = (1 - z_t)\)，\(b_t = z_t \odot \tilde{h}_t\)。

• 对于minLSTM，递归关系可以表示为：

\[h_t = f_t \odot h_{t-1} + i_t \odot \tilde{h}_t\]

其中，\(a_t = f_t\)，\(b_t = i_t \odot \tilde{h}_t\)。

通过并行前缀扫描算法，minGRU和minLSTM可以在训练时完全并行化，避免了传统RNN的逐时间步反向传播（BPTT），显著提高了训练效率。

4. 数值稳定性优化

为了提高数值稳定性，论文提出了对数空间实现（Log-Space Implementation）。具体来说：

• 对于minGRU，对数空间中的递归关系为：

\[\begin{aligned} \log(a_t) &= -\text{Softplus}(\text{Linear}_{dh}(x_t)) \\ \log(b_t) &= \log(z_t) + \log(\tilde{h}_t) \\ \log(h_t) &= \log(a_t) + \log(b_t) \end{aligned}\]

其中，\(\log(z_t) = -\text{Softplus}(-\text{Linear}_{dh}(x_t))\)。

• 对于minLSTM，对数空间中的递归关系为：

\[\begin{aligned} \log(a_t) &= -\text{Softplus}(\text{Linear}_{dh}(x_t)) \\ \log(b_t) &= \log(i_t) + \log(\tilde{h}_t) \\ \log(h_t) &= \log(a_t) + \log(b_t) \end{aligned}\]

其中，\(\log(i_t) = -\text{Softplus}(-\text{Linear}_{dh}(x_t))\)。

通过在对数空间中计算并行前缀扫描，minGRU和minLSTM的数值稳定性得到了显著提高。

5. 实验验证

论文在多种任务上验证了minLSTM和minGRU的性能，包括选择性复制任务、强化学习任务和语言建模任务。实验结果表明，minLSTM和minGRU在这些任务上与现代复杂模型（如Mamba和Transformer）相当，甚至在某些情况下更优。

总结

论文通过简化传统RNN模型（LSTM和GRU），提出了新的最小化版本（minLSTM和minGRU），实现了训练时的完全并行化，同时显著减少了参数量。这些最小化版本在多种任务上表现出色，挑战了当前社区对复杂架构的偏好。通过并行前缀扫描算法和对数空间实现，论文确保了模型的训练效率和数值稳定性。

原文翻译

RNNs是我们所需要的全部吗？

Leo Feng

Mila – Université de Montréal & Borealis AI

leo.feng@mila.quebec

Frederick Tung

Borealis AI

frederick.tung@borealisai.com

Mohamed Osama Ahmed

Borealis AI

mohamed.o.ahmed@borealisai.com

Yoshua Bengio

Mila – Université de Montréal

yoshua.bengio@mila.quebec

Hossein Hajimirsadeghi

Borealis AI

hossein.hajimirsadeghi@borealisai.com

摘要

2017年，Transformer的引入重塑了深度学习的格局。最初提出用于序列建模的Transformer，随后在各个领域取得了广泛的成功。然而，Transformer的可扩展性限制——尤其是在序列长度方面——引发了人们对新型可并行化训练、性能相当且更有效扩展的循环模型的重新兴趣。在这项工作中，我们从历史的角度重新审视序列建模，重点关注在Transformer崛起之前主导该领域二十年的循环神经网络（RNNs）。具体来说，我们研究了LSTM（1997）和GRU（2014）。我们展示了通过简化这些模型，可以推导出最小化版本（minLSTM和minGRU），这些版本（1）比传统版本使用更少的参数，（2）在训练期间完全可并行化，（3）在一系列任务上取得了令人惊讶的竞争力表现，与包括Transformer在内的最新模型相媲美。

1 引言

自20世纪90年代以来，循环神经网络（RNNs）（Elman, 1990），如长短期记忆网络（LSTM）（Hochreiter & Schmidhuber, 1997）和后来的门控循环单元（GRUs）（Cho et al., 2014），一直是序列建模任务（如机器翻译和文本生成）的首选方法。然而，它们固有的顺序性质限制了并行化，使得这些模型在计算上效率低下，并且在长序列上训练速度过慢，这是现实应用中的常见挑战。

2017年，Transformer（Vaswani et al., 2017）通过自注意力机制引入了可并行化的训练机制，彻底改变了深度学习，在序列建模中取得了立竿见影的成功。这一突破导致了流行的大型语言模型的开发，并迅速扩展到其他领域，包括计算机视觉（Dosovitskiy et al., 2021）、强化学习（Chen et al., 2021）和生物信息学（Jumper et al., 2021）。然而，尽管自注意力机制能够有效地建模token之间的交互，但它存在二次计算复杂性的问题，使得Transformer在处理长序列时成本过高，尤其是在资源受限的环境中。为了解决这一问题，许多方法专注于提高Transformer的效率，探索了稀疏性（Kitaev et al., 2019）、低秩近似（Wang et al., 2020）和分块（Dao et al., 2022）等思路。

最近，Transformer的可扩展性限制引发了对替代方法的新兴趣：可并行化且更有效扩展的新型循环模型。在这一领域出现了几种有前景的方法，包括状态空间模型（Gu et al., 2021）、线性化注意力（Peng et al., 2023）以及最近的线性循环神经网络（Orvieto et al., 2023）。值得注意的是，这些最先进的循环模型利用输入依赖的转换，并展示了与Transformer相似的强大性能。这些方法不仅在扩展到大型语言模型方面取得了成功，还扩展到其他领域，如图像（Zhu et al., 2024a）和图数据（Wang et al., 2024a）。

在这项工作中，我们从历史的角度重新审视序列建模，重点关注在Transformer崛起之前主导该领域二十年的RNNs。具体来说，我们探索了LSTM（1997）和GRU（2014），它们是输入依赖循环模型的早期示例。我们展示了通过移除其门控对先前状态的依赖，可以并行训练这些模型。进一步的简化导致了最小化版本（minLSTM和minGRU），这些版本（1）比传统版本使用更少的参数，（2）在训练期间完全可并行化，（3）尽管简单，但在一系列任务上取得了令人惊讶的竞争力表现，挑战了社区中增加架构和算法复杂性的主流趋势。在附录中，我们提供了minGRU和minLSTM的PyTorch实现，仅需几行代码，使得这些模型轻量且高度适应初学者、从业者和研究人员。

2 背景

在本节中，我们回顾传统的循环神经网络（RNN）。RNN是一种序列模型，它在时间步长上维护一个隐藏状态，以捕捉时间依赖性。因此，它们特别适合处理涉及序列数据的任务，如时间序列预测、自然语言处理，以及其他需要根据先前步骤的上下文来指导当前预测的任务。然而，标准RNN（Elman，1990）面临着梯度消失和梯度爆炸的挑战，这限制了它们学习长期依赖关系的能力。

2.1 长短期记忆网络（LSTM）

为了解决这些问题，Hochreiter和Schmidhuber（1997）引入了长短期记忆（LSTM）网络。LSTM是一种非常成功的RNN类型，专门设计用于缓解梯度消失问题，使模型能够有效地捕捉长期依赖关系。LSTM的计算方式如下：

（隐藏状态）

\[\boldsymbol{h}_t = \boldsymbol{o}_t \odot \tanh(\boldsymbol{c}_t)\]

（输出门）

\[\boldsymbol{o}_t = \sigma(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}]))\]

（细胞状态更新）

\[\boldsymbol{c}_t = \boldsymbol{f}_t \odot \boldsymbol{c}_{t - 1} + \boldsymbol{i}_t \odot \tilde{\boldsymbol{c}}_t\]

（遗忘门）

\[\boldsymbol{f}_t = \sigma(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}]))\]

（输入门）

\[\boldsymbol{i}_t = \sigma(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}]))\]

（候选细胞状态）

\[\tilde{\boldsymbol{c}}_t = \tanh(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}]))\]

其中，\(\odot\) 表示向量的逐元素乘法，\(t\) 是当前时间步，\(\boldsymbol{h}_t\) 是输出的隐藏状态。\([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}]\) 表示时间步 \(t\) 的输入向量 \(\boldsymbol{x}_t\) 与前一个隐藏状态 \(\boldsymbol{h}_{t - 1}\) 的连接。\(d_h\) 表示隐藏状态的大小，\(\boldsymbol{c}_t\) 是细胞状态，它在时间步之间传递信息，\(\tilde{\boldsymbol{c}}_t\) 是将被添加到细胞状态的候选细胞状态。

门 \(\boldsymbol{i}_t\)、\(\boldsymbol{f}_t\) 和 \(\boldsymbol{o}_t\) 控制信息在LSTM中的流动。输入门 \(\boldsymbol{i}_t\) 决定从候选细胞状态 \(\tilde{\boldsymbol{c}}_t\) 中添加多少新信息到细胞状态 \(\boldsymbol{c}_t\) 中。遗忘门 \(\boldsymbol{f}_t\) 决定前一个细胞状态 \(\boldsymbol{c}_{t - 1}\) 中的哪一部分应该被丢弃。输出门 \(\boldsymbol{o}_t\) 决定细胞状态中的哪些信息应该作为隐藏状态 \(\boldsymbol{h}_t\) 输出。\(\sigma\)（sigmoid）和 \(\tanh\) 函数用于缩放值，确保在训练过程中输出不会爆炸或消失。一个LSTM模块同时维护一个细胞状态和一个隐藏状态，总共有 \(O(4d_h(d_x + d_h))\) 个参数，其中 \(d_x\) 是输入大小。

2.2 门控循环单元（GRU）

为简化LSTM，Cho 等人（2014）引入了门控循环单元（GRU）。与LSTM的三个门和两个状态（隐藏状态和细胞状态）不同，GRU仅使用两个门和一个单一状态（隐藏状态）。这种复杂度的降低使得GRU能够实现更快的训练和推理速度，同时在许多任务上仍具有竞争力。GRU的计算方式如下：

（隐藏状态更新）

\[\boldsymbol{h}_t = (1 - \boldsymbol{z}_t) \odot \boldsymbol{h}_{t - 1} + \boldsymbol{z}_t \odot \tilde{\boldsymbol{h}}_t\]

（更新门）

\[\boldsymbol{z}_t = \sigma(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}]))\]

（重置门）

\[\boldsymbol{r}_t = \sigma(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}]))\]

（候选隐藏状态）

\[\tilde{\boldsymbol{h}}_t = \tanh(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{r}_t \odot \boldsymbol{h}_{t - 1}]))\]

其中，\(\tilde{\boldsymbol{h}}_t\) 表示候选隐藏状态，即隐藏状态的一个潜在新值。GRU将LSTM的遗忘门和输入门合并为一个单一的更新门 \(\boldsymbol{z}_t \in (0, 1)\)，该更新门决定应该向前传递多少过去的信息（即 \(1 - \boldsymbol{z}_t\)），以及应该添加多少来自候选隐藏状态的新信息（即 \(\boldsymbol{z}_t\)）。此外，GRU去掉了LSTM的输出门，并引入了一个重置门 \(\boldsymbol{r}_t\)，它控制在计算候选隐藏状态 \(\tilde{\boldsymbol{h}}_t\) 时，过去隐藏状态 \(\boldsymbol{h}_{t - 1}\) 的使用量。

通过减少门和状态的数量，GRU也减少了参数和计算的总数，仅需要 \(O(3d_h(d_x + d_h))\) 个参数。然而，GRU和LSTM仍然只是序列模型。因此，它们在训练期间需要通过时间反向传播（BPTT），这导致训练时间呈线性增长，并限制了它们处理长文本上下文的能力。

2.3 并行扫描

由于这种限制，2017 年Transformer的引入彻底改变了该领域，它取代了LSTM和GRU，成为序列建模的实际方法。Transformer在训练期间利用并行化，克服了传统循环模型的顺序瓶颈。然而，Transformer在序列长度方面具有二次复杂度，这限制了它们处理极长上下文的能力，尤其是在资源受限的情况下。

作为回应，新的循环序列模型重新兴起，为Transformer提供了替代方案。这些模型在能够并行训练的同时实现了可比的性能，并且避免了困扰传统RNN（如LSTM和GRU）的通过时间反向传播（BPTT）问题。在这些创新中，许多架构依赖并行前缀扫描算法（Blelloch，1990）来进行高效训练。

并行扫描算法是一种并行计算方法，用于通过结合律运算符\(\oplus\)（例如，\(+\) 和 \(\times\)）从\(N\)个顺序数据点计算\(N\)个前缀计算。该算法可以根据输入序列\(\{u_k\}_{k = 1}^N\)高效地计算前缀和序列\(\{\bigoplus_{i = 1}^k u_i\}_{k = 1}^N\)。并行扫描算法的一个重要应用是计算一类常见的递推关系，形式为\(v_t = a_tv_{t - 1} + b_t\)，其中\(v_t\)、\(a_t\) 和 \(b_t\) 是实数，且\(v_0 \leftarrow b_0\)（Martin & Cundy，2018）。该方法将序列\(a_1, \ldots, a_n\) 和 \(b_0, b_1, \ldots, b_n\) 作为输入，并并行计算序列\(v_1, \ldots, v_n\)。这种方法自然地扩展到向量值的递推关系，例如\(\boldsymbol{v}_t = \boldsymbol{a}_t \odot \boldsymbol{v}_{t - 1} + \boldsymbol{b}_t\)，其中\(\odot\)表示逐元素乘法。

3 方法

有趣的是，我们可以看到GRU的隐藏状态更新和LSTM的细胞状态更新与向量公式相似。在本节中，我们证明通过从GRU和LSTM的各种门中去除对先前状态的依赖，它们可以通过并行扫描进行训练。在此基础上，我们通过去除它们对输出范围的限制（即\(\tanh\)函数）进一步简化这些RNN。结合这些步骤，我们描述了可以并行训练的GRU和LSTM的最简版本（minGRU和minLSTM）。

3.1 最简GRU：minGRU

3.1.1 步骤1：从门中去除对先前状态的依赖

回顾一下GRU的隐藏状态更新公式如下：

\[\boldsymbol{h}_t = (1 - \boldsymbol{z}_t) \odot \boldsymbol{h}_{t - 1} + \boldsymbol{z}_t \odot \tilde{\boldsymbol{h}}_t\]

我们可以观察到，这种更新类似于前面提到的并行扫描公式\(\boldsymbol{v}_t = \boldsymbol{a}_t \odot \boldsymbol{v}_{t - 1} + \boldsymbol{b}_t\)，其中\(\boldsymbol{a}_t \leftarrow (1 - \boldsymbol{z}_t)\)，\(\boldsymbol{b}_t \leftarrow \boldsymbol{z}_t \odot \tilde{\boldsymbol{h}}_t\)，\(\boldsymbol{v}_t \leftarrow \boldsymbol{h}_t\)。然而，\(\boldsymbol{z}_t\) 和 \(\tilde{\boldsymbol{h}}_t\) 依赖于前一个隐藏状态 \(\boldsymbol{h}_{t - 1}\)，即\(\boldsymbol{z}_t = \sigma(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}]))\) 且 \(\tilde{\boldsymbol{h}}_t = \tanh(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{r}_t \odot \boldsymbol{h}_{t - 1}]))\)。因此，不能直接应用并行扫描，因为该算法的输入\(\boldsymbol{a}_1, \ldots, \boldsymbol{a}_n\) 和 \(\boldsymbol{b}_1, \ldots, \boldsymbol{b}_n\) 依赖于已经知道的输出\(\boldsymbol{h}_1, \ldots, \boldsymbol{h}_{n - 1}\)。

一个简单的解决方法是通过去除对前一个隐藏状态（即\(\boldsymbol{h}_{t - 1}\)）的依赖来简化GRU。具体的变化如下：

\[\begin{align*} \boldsymbol{z}_t = \sigma(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}])) &\Rightarrow \boldsymbol{z}_t = \sigma(\text{Linear}_{d_h}(\boldsymbol{x}_t))\\ \boldsymbol{r}_t = \sigma(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}])) &\\ \tilde{\boldsymbol{h}}_t = \tanh(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{r}_t \odot \boldsymbol{h}_{t - 1}])) &\Rightarrow \tilde{\boldsymbol{h}}_t = \tanh(\text{Linear}_{d_h}(\boldsymbol{x}_t)) \end{align*}\]

通过从候选隐藏状态 \(\tilde{\boldsymbol{h}}_t\) 中去除对 \(\boldsymbol{h}_{t - 1}\) 的依赖，原本用于控制 \(\boldsymbol{h}_{t - 1}\) 权重的重置门 \(\boldsymbol{r}_t\) 也不再需要，因此被去除。在没有对先前隐藏状态的依赖后，算法的输入\(\boldsymbol{a}_1, \ldots, \boldsymbol{a}_n\) 和 \(\boldsymbol{b}_1, \ldots, \boldsymbol{b}_n\) 都可以轻松并行计算，从而可以通过并行扫描高效地计算出\(\boldsymbol{h}_1, \ldots, \boldsymbol{h}_n\)。

尽管在理论上有人担心缺少对先前状态的依赖（Merrill 等人，2024），但也有大量的实证证据支持省略这些依赖的模型的有效性，比如xLSTM（Beck 等人，2024）和Mamba（Gu & Dao，2024）。这些循环模型不是通过显式地对先前状态的依赖进行建模来捕捉长距离依赖关系，而是可以通过堆叠多个层来学习这些关系。值得注意的是，在xLSTM论文中，他们的完全并行化版本（xLSTM[1:0]），即消除了隐藏状态依赖的版本，其性能与保留这些依赖的版本（如xLSTM[7:1]）相似，在某些情况下甚至更好。

3.1.2 步骤2：去除候选状态的范围限制

在GRU的隐藏状态更新中，从前一个隐藏状态传递过来的比例\((1 - \boldsymbol{z}_t)\) 与为新候选隐藏状态添加的量\((\boldsymbol{z}_t)\) 之和为1。因此，GRU隐藏状态值的规模与时间无关。相反，其隐藏状态的规模取决于候选隐藏状态\(\tilde{\boldsymbol{h}}_t\) 的规模。双曲正切函数（\(\tanh\)）在LSTM和GRU中起着关键作用，它限制了（候选）隐藏状态的范围，即\(\tilde{\boldsymbol{h}}_t, \boldsymbol{h}_t \in (-1, 1)^{d_h}\) 。\(\tanh\) 函数有助于稳定训练，并缓解由于对隐藏状态的线性变换应用sigmoid（\(\sigma\)）激活函数（例如，\(\boldsymbol{z}_t = \sigma(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}]))\) ）而导致的梯度消失问题。在前面的步骤中，这些隐藏状态的依赖关系已被去除。因此，我们通过如下方式去除对（候选）隐藏状态的范围限制（\(\tanh\) ），进一步简化GRU：

\[\tilde{\boldsymbol{h}}_t = \tanh(\text{Linear}_{d_h}(\boldsymbol{x}_t)) \Rightarrow \tilde{\boldsymbol{h}}_t = \text{Linear}_{d_h}(\boldsymbol{x}_t)\]

3.1.3 minGRU

结合这两个简化步骤，得到了GRU的最简版本（minGRU）：

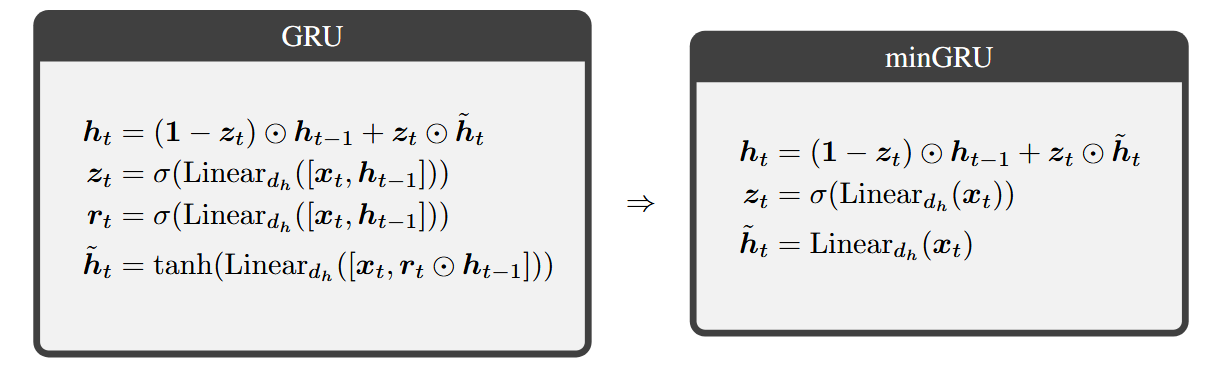
得到的模型比原始GRU高效得多，仅需要\(O(2d_h d_x)\) 个参数，而GRU需要\(O(3d_h(d_x + d_h))\) 个参数，其中\(d_x\) 和\(d_h\) 分别表示输入\(\boldsymbol{x}_t\) 和隐藏状态\(\boldsymbol{h}_t\) 的维度大小。在RNN中，经常会使用状态扩展（即\(d_h = \alpha d_x\) ，其中\(\alpha \geq 1\) ），这有助于模型更好地从输入数据中提取特征。当\(\alpha = 1, 2, 3, 4\) 时，minGRU分别使用GRU参数的约33%、22%、17%和13%。

此外，现在GRU的最简版本可以使用并行扫描算法进行并行训练，无需通过时间反向传播（BPTT）。附录中包含了伪代码和一个简单的PyTorch实现。

3.2.1 步骤1：从门中去除对先前状态的依赖

回顾LSTM的细胞状态更新公式如下：

\[\boldsymbol{c}_t = \boldsymbol{f}_t \odot \boldsymbol{c}_{t - 1} + \boldsymbol{i}_t \odot \tilde{\boldsymbol{c}}_t\]

与GRU的隐藏状态类似，我们可以看到LSTM的细胞状态更新类似于前面提到的并行扫描公式\(\boldsymbol{v}_t = \boldsymbol{a}_t \odot \boldsymbol{v}_{t - 1} + \boldsymbol{b}_t\) ，其中\(\boldsymbol{a}_t \leftarrow \boldsymbol{f}_t\)，\(\boldsymbol{b}_t \leftarrow \boldsymbol{i}_t \odot \tilde{\boldsymbol{c}}_t\)，\(\boldsymbol{v}_t \leftarrow \boldsymbol{c}_t\) 。然而，\(\boldsymbol{f}_t\)，\(\boldsymbol{i}_t\) 和 \(\tilde{\boldsymbol{c}}_t\) 依赖于前一个隐藏状态 \(\boldsymbol{h}_t\) 。因此，LSTM的细胞状态更新不能直接应用并行扫描算法。我们可以采用与GRU类似的方式，通过如下方式去除对隐藏状态的依赖：

\[\begin{align*} \boldsymbol{f}_t = \sigma(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}])) &\Rightarrow \boldsymbol{f}_t = \sigma(\text{Linear}_{d_h}(\boldsymbol{x}_t))\\ \boldsymbol{i}_t = \sigma(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}])) &\Rightarrow \boldsymbol{i}_t = \sigma(\text{Linear}_{d_h}(\boldsymbol{x}_t))\\ \tilde{\boldsymbol{c}}_t = \tanh(\text{Linear}_{d_h}([\boldsymbol{x}_t, \boldsymbol{h}_{t - 1}])) &\Rightarrow \tilde{\boldsymbol{c}}_t = \tanh(\text{Linear}_{d_h}(\boldsymbol{x}_t)) \end{align*}\]

3.2.2 步骤2：去除候选状态的范围限制

与GRU类似，LSTM利用双曲正切函数（\(\tanh\)）将其状态范围限制在\((-1, 1)\) 之间。LSTM应用了两次范围限制：一次是在计算候选细胞状态时，另一次是在计算隐藏状态时。在这一步中，我们如下去除这两次限制：

\[\begin{align*} \tilde{\boldsymbol{c}}_t = \tanh(\text{Linear}_{d_h}(\boldsymbol{x}_t)) &\Rightarrow \tilde{\boldsymbol{c}}_t = \text{Linear}_{d_h}(\boldsymbol{x}_t)\\ \boldsymbol{h}_t = \boldsymbol{o}_t \odot \tanh(\boldsymbol{c}_t) &\Rightarrow \boldsymbol{h}_t = \boldsymbol{o}_t \odot \boldsymbol{c}_t \end{align*}\]

3.2.3 步骤3：简化输出的缩放

延续简化的思路，我们去掉用于缩放隐藏状态的输出门 \(\boldsymbol{o}_t\) 。没有输出门时，归一化后的隐藏状态等于细胞状态，即\(\boldsymbol{h}_t = \boldsymbol{o}_t \odot \boldsymbol{c}_t \Rightarrow \boldsymbol{h}_t = \boldsymbol{c}_t\) ，这使得同时拥有隐藏状态和细胞状态变得不必要。因此，我们进行如下修改：

\[\begin{align*} \boldsymbol{h}_t = \boldsymbol{o}_t \odot \boldsymbol{c}_t \\ \boldsymbol{o}_t = \sigma(\text{Linear}_{d_h}(\boldsymbol{x}_t)) &\Rightarrow \begin{cases} \boldsymbol{h}_t = \boldsymbol{f}_t \odot \boldsymbol{h}_{t - 1} + \boldsymbol{i}_t \odot \tilde{\boldsymbol{h}}_t\\ \tilde{\boldsymbol{h}}_t = \text{Linear}_{d_h}(\boldsymbol{x}_t) \end{cases}\\ \boldsymbol{c}_t = \boldsymbol{f}_t \odot \boldsymbol{c}_{t - 1} + \boldsymbol{i}_t \odot \tilde{\boldsymbol{c}}_t \\ \tilde{\boldsymbol{c}}_t = \text{Linear}_{d_h}(\boldsymbol{x}_t) \end{align*}\]

在许多序列建模场景（例如文本生成）中，优化目标/指标在规模上与时间无关。回顾LSTM的细胞状态更新公式\(\boldsymbol{c}_t = \boldsymbol{f}_t \odot \boldsymbol{c}_{t - 1} + \boldsymbol{i}_t \odot \tilde{\boldsymbol{c}}_t\) ，其中\(\boldsymbol{i}_t, \boldsymbol{f}_t \in (0, 1)^{d_h}\) ，以及GRU的隐藏状态更新公式¹ \(\boldsymbol{h}_t^{GRU} = (1 - \boldsymbol{z}_t) \odot \boldsymbol{h}_{t - 1}^{GRU} + \boldsymbol{z}_t \odot \tilde{\boldsymbol{h}}_t^{GRU}\) ，其中\(\boldsymbol{z}_t \in (0, 1)^{d_h}\) 。GRU保留前一个隐藏状态的\((1 - \boldsymbol{z}_t) \in (0, 1)\) 部分，并添加新候选状态的 \(\boldsymbol{z}_t\) 部分。由于这些比例之和为1，模型确保其输出（即隐藏状态）在规模上与时间无关。相比之下，LSTM的遗忘门和输入门是独立计算的（例如，\(\boldsymbol{f}_t, \boldsymbol{i}_t \to 1\) 或 \(\boldsymbol{f}_t, \boldsymbol{i}_t \to 0\)），这使得其状态在规模上与时间相关² 。对于时间无关性很重要的任务，我们可以通过简单地对LSTM的输入门和遗忘门进行归一化来确保其输出在规模上与时间无关，即\(\boldsymbol{f}_t', \boldsymbol{i}_t' \leftarrow \frac{\boldsymbol{f}_t}{\boldsymbol{f}_t + \boldsymbol{i}_t}, \frac{\boldsymbol{i}_t}{\boldsymbol{f}_t + \boldsymbol{i}_t}\) ，确保\(\boldsymbol{f}_t' + \boldsymbol{i}_t' = 1\) ，并且LSTM状态的规模与时间无关。

3.2.4 最简LSTM（minLSTM）

结合上述三个步骤，得到了LSTM的最简版本（minLSTM）：

通过隐藏状态更新公式\(\boldsymbol{h}_t = \boldsymbol{f}_t' \odot \boldsymbol{h}_{t - 1} + \boldsymbol{i}_t' \odot \tilde{\boldsymbol{h}}_t\) ，并使用归一化的遗忘门 \(\boldsymbol{f}_t'\) 和输入门 \(\boldsymbol{i}_t'\)（计算方式为\(\boldsymbol{f}_t', \boldsymbol{i}_t' \leftarrow \frac{\boldsymbol{f}_t}{\boldsymbol{f}_t + \boldsymbol{i}_t}, \frac{\boldsymbol{i}_t}{\boldsymbol{f}_t + \boldsymbol{i}_t}\) ），可以实现与时间无关的输出。

所得模型比原始LSTM高效得多，与LSTM的\(O(4d_h(d_x + d_h))\) 个参数相比，它仅需要\(O(3d_h d_x)\) 个参数。考虑到状态扩展（即\(d_h = \alpha d_x\) ，其中\(\alpha \geq 1\) ），当\(\alpha = 1, 2, 3\) 或\(4\) 时，minLSTM分别使用LSTM参数的约38%、25%、19%或15%。

此外，LSTM的最简版本现在可以使用并行扫描算法进行并行训练，无需通过时间反向传播（BPTT）。附录中包含了伪代码和一个简单的PyTorch实现。

4 RNN是我们所需要的全部吗？

在本节中，我们将最简版本（minLSTM和minGRU）与它们的传统版本（LSTM和GRU）以及现代序列模型进行比较。附录中提供了伪代码、PyTorch实现以及关于实验设置的详细信息。

4.1 最简LSTM和GRU效率高

在测试时，循环序列模型通常按顺序展开，这使得推理相对高效。然而，传统RNN的主要瓶颈在于其训练过程，训练需要通过时间反向传播（BPTT），计算效率低下。这也是许多早期基于RNN的模型最终被弃用的原因之一。

在本节中，我们比较了训练传统RNN（LSTM和GRU）、它们的简化版本（minLSTM和minGRU）³ 以及Mamba（使用官方实现，Mamba是一种最近流行的循环序列模型）所需的资源。

对于这些实验，使用固定的批量大小64，同时改变序列长度。我们测量了进行前向传播、计算损失以及进行反向传播以计算梯度所涉及的总运行时间和内存复杂度。为确保公平直接的比较，所有模型都在相同的层数下进行测试。

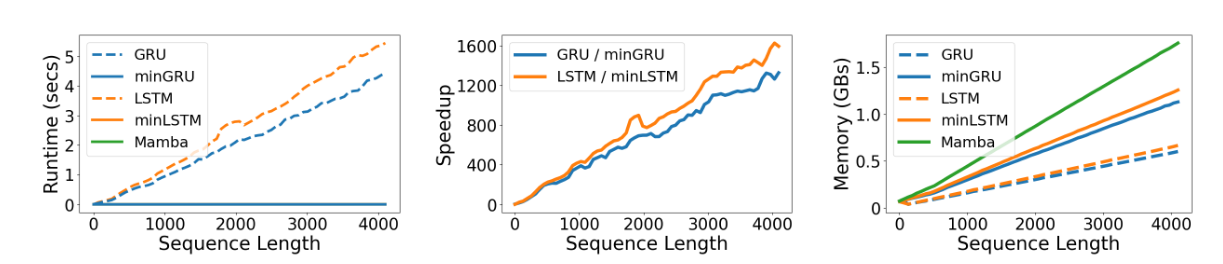
图1：T4 GPU上的训练运行时间（左）、加速比（中）和内存占用（右），批次大小为64。在训练运行时间图（左）中，minGRU、minLSTM和Mamba的线条重叠。这些方法在训练运行时间上大致相同。

运行时间：我们需要强调的是，推理速度可能因硬件和实现方式而异。PyTorch的内置RNN是经过高度优化的底层GPU实现。为了公平比较，在这些实验中，minGRU、minLSTM、GRU和LSTM都是用普通PyTorch编写的。在运行时间方面（见图1左侧），LSTM和GRU的简化版本（minLSTM和minGRU）与Mamba的运行时间相近。在100次运行中取平均值，对于序列长度为512，minLSTM、minGRU和Mamba的运行时间分别为2.97、2.72和2.71毫秒。对于序列长度为4096，运行时间分别为3.41、3.25和3.15毫秒。相比之下，传统的RNN版本（LSTM和GRU）的运行时间与序列长度呈线性关系。对于序列长度为512，minGRU和minLSTM在每个训练步骤上的速度分别比GRU和LSTM快175倍和235倍（见图1中间）。随着序列长度的增加，这种提升更加显著，当序列长度为4096时，minGRU和minLSTM的速度分别快1324倍和1361倍。因此，在minGRU完成固定轮数训练需要一天的情况下，其传统版本GRU可能需要3年时间。

图1：T4 GPU上的训练运行时间（左）、加速比（中）和内存占用（右），批次大小为64。在训练运行时间图（左）中，minGRU、minLSTM和Mamba的线条重叠。这些方法在训练运行时间上大致相同。

内存：通过利用并行扫描算法来高效并行计算输出，minGRU、minLSTM和Mamba创建了更大的计算图，因此与传统RNN相比需要更多内存（见图1右侧）。最简变体（minGRU和minLSTM）相比它们的传统版本（GRU和LSTM）多使用约88%的内存。Mamba相比minGRU多使用56%的内存。然而在实际应用中，运行时间通常是训练RNN时的瓶颈。

去除 \(\boldsymbol{h}_{t - 1}\) 的影响

原始的LSTM和GRU使用输入 \(\boldsymbol{x}_t\) 和前一个隐藏状态 \(\boldsymbol{h}_{t - 1}\) 来计算各种门。这些模型利用与时间相关的门来学习复杂函数。然而，minLSTM和minGRU通过去除门对前一个隐藏状态 \(\boldsymbol{h}_{t - 1}\) 的依赖，实现了训练效率的提升。因此，minLSTM和minGRU的门仅依赖于输入 \(\boldsymbol{x}_t\)，这使得循环模块更加简单。这样一来，由单层minLSTM或minGRU组成的模型的门与时间无关，因为它们基于与时间无关的输入 \(\boldsymbol{x}_{1:n}^{(1)}\)。

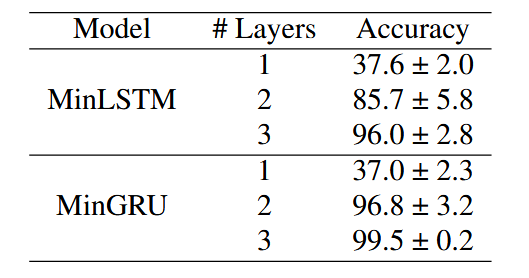
表1：选择性复制任务（Gu & Dao, 2024）上的层数比较。

然而，在深度学习中，模型是通过堆叠模块构建的。尽管第一层的输入 \(\boldsymbol{x}_{1:n}^{(1)}\) 与时间无关，但其输出 \(\boldsymbol{h}_{1:n}^{(1)}\) 与时间相关，并作为第二层的输入，即 \(\boldsymbol{x}_{1:n}^{(2)} \leftarrow \boldsymbol{h}_{1:n}^{(1)}\)。因此，从第二层开始，minLSTM和minGRU的门也将与时间相关，从而能够对更复杂的函数进行建模。在表1中，我们根据Mamba论文（Gu & Dao，2024）中的选择性复制任务，比较了不同层数模型的性能。我们可以立即看到时间相关性的影响：将层数增加到2层或更多会显著提升性能。

训练稳定性

表1：选择性复制任务（Gu & Dao, 2024）上的层数比较。

层数的另一个影响是，随着层数的增加，准确性的方差会减小，稳定性会提高（见表1）。此外，虽然minLSTM和minGRU都能解决选择性复制任务，但我们可以看到，在经验上minGRU比minLSTM更稳定，它能更一致地完成任务，且方差更低。minLSTM丢弃旧信息并添加新信息，通过两组参数（遗忘门和输入门）控制比例。在训练过程中，这两组参数会朝着不同方向调整，使得比例更难控制和优化。相比之下，minGRU丢弃和添加信息的过程由一组参数（更新门）控制。

4.2 最简循环神经网络（RNN）表现惊人

在本节中，我们聚焦于几十年前提出的模型LSTM（1997年）和GRU（2014年）的最简版本的实证性能，并将它们与几种现代序列模型进行比较。需要注意的是，我们这项工作的主要目标不是在特定任务上取得最佳性能，而是要证明简化传统架构能够产生具有竞争力的结果，可与近期的序列模型相媲美。

选择性复制任务：我们首先来看选择性复制任务，该任务最初在具有影响力的Mamba论文（Gu & Dao，2024）中提出。这个任务是一个关键基准，展示了Mamba的状态空间模型S6相较于以前的先进模型（如S4（Gu等人，2021）和Hyena（Poli等人，2023））所做出的改进。该任务要求模型进行基于内容的推理，它们必须有选择地记住相关的标记，同时过滤掉不相关的标记。

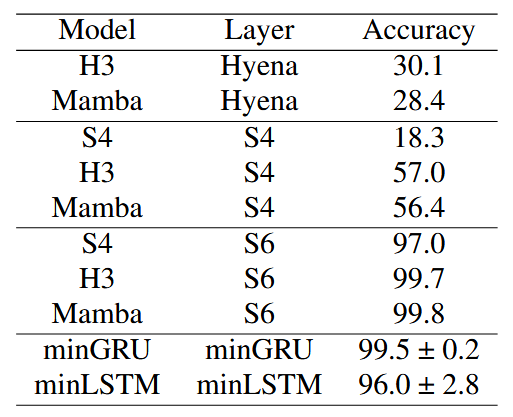
表2：选择性复制任务。minLSTM、minGRU和Mamba的S6（Gu & Dao, 2024）能够解决该任务。其他方法如S4、H3和Hyena最多只能部分解决该任务。

在表2中，我们将简化版本的LSTM和GRU（minLSTM和minGRU）与几种可以并行训练的知名循环序列模型进行比较，这些模型包括S4（Gu等人，2021）、H3（Fu等人，2023）、Hyena（Poli等人，2023）和Mamba（S6）（Gu & Dao，2024）。这些基线模型的结果直接引自Mamba论文。值得注意的是，只有Mamba的S6模型成功解决了这个任务。

minGRU和minLSTM也都能够很好地解决选择性复制任务，取得了与S6相当的性能，并且超过了其他现代基线模型，这凸显了这些利用基于内容的门控机制的传统模型（LSTM和GRU）的有效性。

强化学习：接下来，我们考虑来自D4RL基准（Fu等人，2020）的MuJoCo运动任务。具体来说，我们研究三个环境：半猎豹（HalfCheetah）、跳跃者（Hopper）和步行者（Walker）。对于每个环境，模型在三个不同数据质量的数据集上进行训练：中等质量（M）、中等重放质量（M - R）和中等专家质量（M - E）。

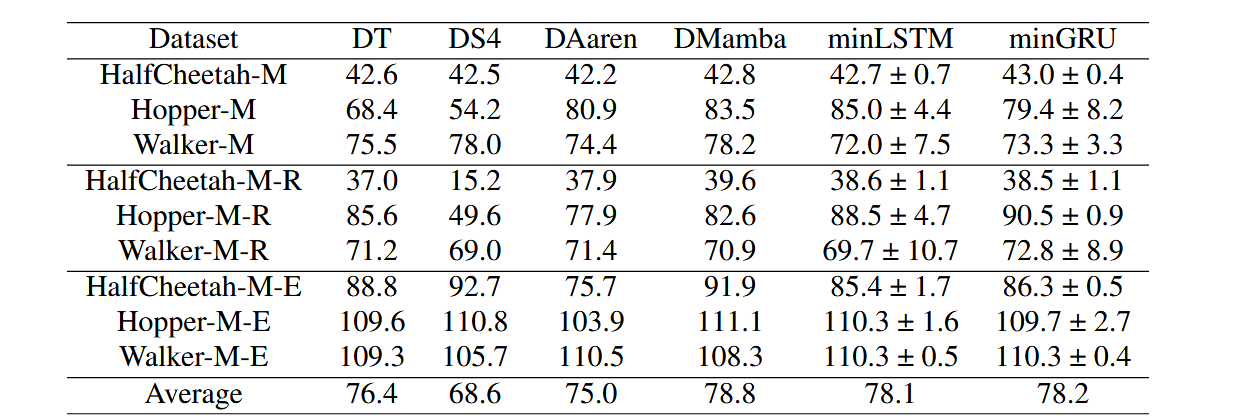
表3：D4RL（Fu et al., 2020）数据集上的强化学习结果。我们报告了专家归一化回报（越高越好），遵循（Fu et al., 2020），并在五个随机种子上的平均值。LSTM和GRU的最小化版本minLSTM和minGRU优于Decision S4（David et al., 2023），并与Decision Mamba（Ota, 2024）、(Decision) Aaren（Feng et al., 2024）和Decision Transformer（Chen et al., 2021）表现相当。

在表3中，我们将minLSTM和minGRU与各种决策Transformer变体进行比较，包括原始的决策Transformer（DT）（Chen等人，2021）、决策S4（DS4）（David等人，2023）、决策Mamba（Ota，2024）和（决策）Aaren（Feng等人，2024）。基线结果从决策Mamba和Aaren的论文中获取。minLSTM和minGRU的性能优于决策S4，并且与决策Transformer、Aaren和Mamba的性能相当。与其他循环方法不同，决策S4是一个其循环转换不依赖于输入的模型，这影响了其性能。在3×3 = 9个数据集的平均得分方面，minLSTM和minGRU的性能超过了除决策Mamba之外的所有基线模型，与决策Mamba的差异很小。

语言建模

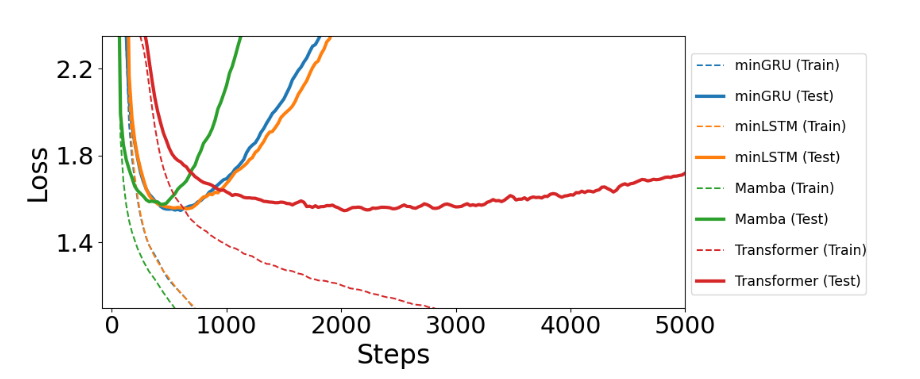
图2：Shakespeare数据集上的语言建模结果。几十年前的RNN（LSTM和GRU）的最小化版本与Mamba和Transformer表现相当。Transformer需要约2.5倍的训练步骤才能达到相当的性能，最终出现过拟合。

最后，我们考虑一个语言建模任务。在这个任务中，我们使用nanoGPT（Karpathy，2022）框架，基于莎士比亚的作品训练一个字符级的GPT模型。在图2中，我们绘制了学习曲线和交叉熵损失，比较了提出的最简LSTM和GRU（minLSTM和minGRU）与Mamba和Transformer的表现。我们发现，minGRU、minLSTM、Mamba和Transformer的测试损失分别为1.548、1.555、1.575和1.547，性能相当。Mamba的表现略逊于其他模型，但训练速度更快，尤其是在早期阶段，它在400步时达到最佳性能，而minGRU和minLSTM则分别持续训练到575步和625步。相比之下，Transformer的训练速度明显较慢，要达到相当的性能，需要比minGRU多2000步（约2.5倍）的训练步骤，这使得它的训练速度明显更慢，且资源消耗更大（与minGRU、minLSTM和Mamba的线性复杂度相比，Transformer具有二次复杂度） 。

5 相关工作

在本节中，我们简要概述了近年来表现出强大性能的高效循环序列模型，这些模型在可扩展性方面优于Transformer，同时提供了更好的可扩展性。关于高效循环模型复兴的更全面讨论，我们建议读者参考最近的综述（Tiezzi et al., 2024）。总体而言，这些模型在三个关键方向上取得了进展：

深度状态空间模型（SSMs）

基于连续时间线性系统，Gu et al. (2021) 提出了S4，这是一种状态空间模型，可以在推理时像RNN一样展开，并像卷积神经网络一样进行训练。S4的成功为该领域的后续发展铺平了道路（Gu et al., 2022; Gupta et al., 2022; Hasani et al., 2023; Smith et al., 2023），并在语言处理（Mehta et al., 2023）和音频分析（Goel et al., 2022）等多个领域得到了应用。最近，Mamba在SSMs中取得了重大突破，超越了之前的模型并引起了广泛关注。Mamba的一个关键创新是引入了S6，这是一种具有输入依赖转换矩阵的状态空间模型，与之前使用输入独立转换矩阵的模型形成对比。Mamba和其他状态空间模型的成功促使了多篇关于该主题的综述发表（Wang et al., 2024b; Patro & Agneeswaran, 2024; Qu et al., 2024）。

循环版本的注意力机制

另一个流行的方向是注意力机制，特别是与线性注意力相关的研究（Katharopoulos et al., 2020）。例如，Sun et al. (2023) 和 Qin et al. (2023) 提出了使用输入独立门控机制（衰减因子）的线性注意力模型。相比之下，Katsch (2023) 和 Yang et al. (2024) 提出了使用输入依赖门控的线性注意力变体。最近，Feng et al. (2024) 展示了softmax注意力也可以被视为RNN，并基于其RNN公式提出了一个循环模型。

可并行化的RNNs

我们的工作与几篇关于并行化RNN的著名论文密切相关。Bradbury et al. (2017) 修改了经典的门控RNN，利用卷积层提高效率，并在时间上应用它们。Martin & Cundy (2018) 证明了具有线性依赖性的RNN可以使用并行扫描进行高效训练。基于这项工作，作者提出了GILR，一种门控线性RNN，其中输出可以作为传统RNN（如LSTM）中先前状态依赖的替代，从而实现并行训练。值得注意的是，minGRU等同于GILR，但没有激活函数。最近，Orvieto et al. (2023) 提出了一种线性门控RNN，利用复杂对角递归和指数参数化，取得了与状态空间模型相当的性能。Qin et al. (2024b) 提出了HGRN，其token mixer HGRU是一种线性门控RNN，增加了复杂值（极坐标）递归、遗忘门的下界和输出门。HGRN2（Qin et al., 2024a）通过引入状态扩展改进了HGRN。Beck et al. (2024) 使用指数门控和归一化状态扩展了LSTM。他们的xLSTM包括可并行化（mLSTM）和仅顺序（sLSTM）版本。mLSTM移除了隐藏状态依赖以实现并行化，引入了矩阵记忆单元，并使用查询向量从记忆中检索。Zhu et al. (2024b) 基于HGRN的见解重新审视了GRU，提出了一种可并行化的token mixer，移除了矩阵乘法并利用三元权重量化。

6 结论

在这项工作中，我们重新审视了序列建模的历史，重点关注了在Transformer模型崛起之前主导该领域二十年的传统RNN，特别是LSTM（1997）和GRU（2014）。我们展示了通过移除门控对先前状态的依赖，可以实现传统RNN的并行训练。进一步的简化导致了最小化版本——minLSTM和minGRU——这些版本具有以下优势：（1）比传统版本使用更少的参数，（2）在训练期间完全可并行化，（3）尽管简单，但在一系列任务上取得了令人惊讶的竞争力表现，与现代模型相媲美。在附录中，我们提供了minGRU和minLSTM的PyTorch实现，仅需几行代码。这使得它们轻量且易于初学者、从业者和研究人员使用。我们希望这项工作能够引发关于序列建模演变的更广泛讨论，鼓励在更复杂架构的背景下重新评估像LSTM和GRU这样的简单基础模型。鉴于这些几十年前的RNN最小化版本的惊人有效性，以及现代RNN架构的最新成功，我们提出了一个问题：“RNNs是我们所需要的全部吗？”

局限性

现代模型如Mamba和xLSTM是在具有80 GB内存的现代A100 GPU上运行的。相比之下，我们的实验是在较旧的GPU（即P100、T4和Quadro 5000）上进行的，这些GPU仅有16 GB内存（约为其他模型可用内存的20%）。这些硬件限制影响了我们进行大规模实验的能力。为了适应内存限制，我们在训练某些任务时使用了梯度累积，将有效批次大小减半，这导致了显著更慢的训练时间。虽然这种方法使我们能够在可用内存限制内运行实验，但也限制了我们的评估规模。

尽管存在这些局限性，我们相信从实验中得出的结论很可能适用于更大规模的设置。传统RNN的最小化版本与许多最近的循环序列模型（如输入依赖门控）具有基本相似性，这表明在给定足够计算资源的情况下，它们在更大数据集上的性能很可能是一致的。