k060, G061 GPU-Accelerated Transparent Point-Based Rendering

Zhangwenniu 于 2025-03-17 发布  |   阅读量: 次

论文链接

ACM Link

发表时间：Published: 30 July 2006

发表于2006 ACM SIGGRAPH

Citation:

@inproceedings{10.1145/1179849.1180072,
author = {Zhang, Yanci and Pajarola, Renato},
title = {GPU-accelerated transparent point-based rendering},
year = {2006},
isbn = {1595933646},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/1179849.1180072},
doi = {10.1145/1179849.1180072},
booktitle = {ACM SIGGRAPH 2006 Sketches},
pages = {178–es},
location = {Boston, Massachusetts},
series = {SIGGRAPH '06}
}@inproceedings{10.1145/1179849.1180072,
author = {Zhang, Yanci and Pajarola, Renato},
title = {GPU-accelerated transparent point-based rendering},
year = {2006},
isbn = {1595933646},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/1179849.1180072},
doi = {10.1145/1179849.1180072},
booktitle = {ACM SIGGRAPH 2006 Sketches},
pages = {178–es},
location = {Boston, Massachusetts},
series = {SIGGRAPH '06}
}

论文重点与难点

1 透明点基渲染的核心问题

论文的核心问题是解决透明点基对象渲染中的两个混合操作冲突：PBR（Point-Based Rendering）插值混合和透明度混合（transparency-compositing）。PBR插值混合用于在屏幕空间内对同一表面层的重叠点进行平滑混合，而透明度混合则用于按从后向前的顺序对表面层进行α混合以生成透明效果。这两个操作的冲突是透明点基渲染的主要难点。

2 算法的核心思想

论文提出了一种新颖的算法，将这两种混合操作分离到不同的渲染阶段。基于图着色算法（graph coloring algorithm），将点集划分为多个组，使得组内点的重叠最小化。对于单个组内的点，省略PBR混合，因为组内点的重叠较小；而透明度混合则在第一阶段针对每个组分别进行。在后处理阶段，通过组合透明度混合阶段的图像来完成PBR混合。

3 预处理阶段的关键点

预处理的目的是将点划分为组，以实现以下两个目标：

最小化重叠分组可以表述为一个K种颜色的加权图着色（K-colors Weighted Graph Coloring, WGC）问题。通过定义加权图\(G(S, E)\)，其中\(S = \{p_1, \dots, p_n\}\)是点集，\(E = \{e_{ij} \vert \text{iff } p_i \text{和} p_j \text{有非零重叠}\}\)是边集，\(W = \{w_{ij} \vert \text{点} p_i \text{和} p_j \text{的重叠}\}\)是权重。目标是为图\(G\)中的每个节点分配K种颜色之一，生成K个子图，同时最小化子图中权重的总和。该问题可以通过两步贪婪策略解决，包括初始化和优化步骤。为了改善表面覆盖，可能需要在组之间复制一些点或增大点的半径。

4 渲染阶段的关键点

渲染阶段的核心是3-pass算法：

1. 最近层的几何阶段（Geometry Pass for Nearest Layer）：使用高质量的PBR混合渲染由WGC算法生成的点组\(S_k\)到目标图像\(F_k\)，包括最近片元的深度（深度缓冲区\(Z\)）和混合核权重信息。

2. 其他层的几何阶段（Geometry Pass for Other Layers）：使用从后向前的透明度α混合渲染点组\(S_k\)到目标图像\(O_k\)，但忽略最近层的所有片元，使用上一步的深度掩码\(Z\)。

3. 合成阶段（Compositing Pass）：根据每个片元的PBR核权重将图像\(F_k\)组合在一起，得到最近可见层的平滑插值图像\(C_F\)；将图像\(O_k\)平均合成\(C_O\)。最终通过α混合\(C_F\)和\(C_O\)实现高质量的透明效果。

5 难点与解决方案

6 算法的优势

7 实验结果

fig.1

图1：渲染结果。a) 不透明和透明对象；b) 折射和反射环境映射，包括菲涅尔效应和色散效果。

论文展示了算法在渲染透明点基对象时的效果，包括不透明和透明对象的混合渲染（图1a），以及折射和反射环境映射的高质量渲染（图1b）。这些结果验证了算法的有效性和实用性。

论文详细讲解

1 研究背景与问题

论文研究的核心问题是透明点基对象的渲染问题。透明点基对象渲染的主要难点在于解决两种混合操作的冲突：PBR插值混合（PBR-interpolation） 和 透明度混合（transparency-compositing）。

这两种混合操作在传统方法中难以同时高效实现，因为PBR插值混合的权重会干扰透明度混合的效果。

2 算法设计

为了解决上述问题，论文提出了一种新颖的算法，将这两种混合操作分离到不同的渲染阶段。算法的核心是基于图着色算法（graph coloring algorithm），将点集划分为多个组，使得组内点的重叠最小化。具体步骤如下：

2.1 预处理阶段（Preprocessing）

预处理阶段的目标是将点集划分为多个组，以实现以下两个目标：

1. 最小化组内点的重叠，以便将PBR混合推迟到图像合成的后处理阶段。

2. 每个组对表面有良好的覆盖，以便进行透明度α混合。

预处理的具体方法是将点集划分问题表述为一个K种颜色的加权图着色（K-colors Weighted Graph Coloring, WGC）问题。定义加权图\(G(S, E)\)，其中：

目标是为图\(G\)中的每个节点分配K种颜色之一，生成K个子图，同时最小化子图中权重的总和。该问题可以通过两步贪婪策略解决，包括初始化和优化步骤。为了改善表面覆盖，可能需要在组之间复制一些点或增大点的半径。

2.2 渲染阶段（Rendering）

渲染阶段的核心是3-pass算法，具体步骤如下：

1. 最近层的几何阶段（Geometry Pass for Nearest Layer）

使用高质量的PBR混合渲染由WGC算法生成的点组\(S_k\)到目标图像\(F_k\)，包括最近片元的深度（深度缓冲区\(Z\)）和混合核权重信息。

2. 其他层的几何阶段（Geometry Pass for Other Layers）

使用从后向前的透明度α混合渲染点组\(S_k\)到目标图像\(O_k\)，但忽略最近层的所有片元，使用上一步的深度掩码\(Z\)。

3. 合成阶段（Compositing Pass）

根据每个片元的PBR核权重将图像\(F_k\)组合在一起，得到最近可见层的平滑插值图像\(C_F\)；将图像\(O_k\)平均合成\(C_O\)。最终通过α混合\(C_F\)和\(C_O\)实现高质量的透明效果。

3 算法优势与效果

论文提出的算法具有以下优势：

fig.1

图1：渲染结果。a) 不透明和透明对象；b) 折射和反射环境映射，包括菲涅尔效应和色散效果。

1. 支持混合渲染：能够正确渲染混合不透明和透明点表面（如图1a所示）。

2. 高质量透明效果：通过分离混合操作，算法能够实现高质量的透明渲染，包括多层折射和反射效果（如图1b所示）。

3. 效率提升：通过将PBR混合推迟到后处理阶段，减少了计算复杂度，提高了渲染效率。

4 实验结果

论文通过实验验证了算法的有效性。实验结果表明：

fig.1

图1：渲染结果。a) 不透明和透明对象；b) 折射和反射环境映射，包括菲涅尔效应和色散效果。

5 总结

论文提出了一种基于图着色算法的透明点基渲染方法，通过分离PBR混合和透明度混合操作，解决了传统方法中的冲突问题。该方法不仅能够实现高质量的透明渲染，还支持混合不透明和透明点表面的渲染，具有较高的实用性和效率。

论文方法部分详细讲解

1 预处理阶段（Preprocessing）

预处理阶段的目标是将点集划分为多个组，以实现以下两个目标：

1.1 问题表述

预处理的核心是将点集划分问题表述为一个K种颜色的加权图着色（K-colors Weighted Graph Coloring, WGC）问题。具体定义如下：

目标是为图 \(G\) 中的每个节点分配 \(K\) 种颜色之一，生成 \(K\) 个子图，同时最小化子图中权重的总和。

1.2 解决方案

该问题通过两步贪婪策略解决：

1. 初始化：为每个点分配一个初始颜色。

2. 优化：通过迭代优化，调整点的颜色分配，以最小化组内重叠。

为了改善表面覆盖，可能需要在组之间复制一些点或增大点的半径。

2 渲染阶段（Rendering）

渲染阶段的核心是3-pass算法，具体步骤如下：

2.1 最近层的几何阶段（Geometry Pass for Nearest Layer）

2.2 其他层的几何阶段（Geometry Pass for Other Layers）

2.3 合成阶段（Compositing Pass）

3 算法优势

4 总结

论文提出的方法通过预处理阶段的图着色算法优化点的分组，并通过3-pass算法分离PBR混合和透明度混合操作，实现了高质量的透明点基渲染。这种方法不仅解决了传统方法中的冲突问题，还支持混合不透明和透明点表面的渲染，具有较高的实用性和效率。

原文翻译

GPU加速的透明点基渲染

Yanci Zhang∗ Renato Pajarola†

可视化与多媒体实验室

苏黎世大学信息学系

1 概述

fig.2

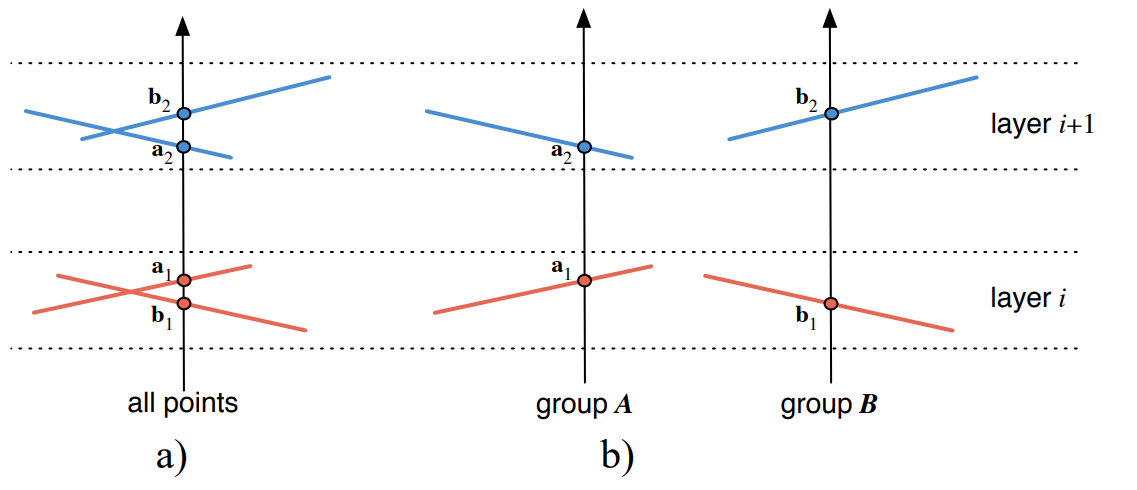
图2：a) 透明点的渲染必须区分每个片段的混合以进行点插值以及透明α混合。b) 我们将点划分为组；其中a1、b1分别在其组内与a2、b2进行透明α混合，然后在后处理阶段执行PBR插值。

渲染透明点基对象的主要难点在于解决两种混合操作之间的冲突：PBR插值和透明合成。PBR插值用于在屏幕空间内混合同一表面层中的重叠splat，以实现平滑的表面渲染；而透明合成则用于按从后到前的顺序α混合表面层，以生成透明效果。我们提出了一种新颖的算法，将这两种混合操作分离到不同的渲染通道中，如图2所示。该方法基于图着色算法，将点集划分为重叠最小的组。对于单个组内的点，由于splat之间的重叠较小，因此省略了PBR混合，而是分别对每个组进行透明混合。在后处理阶段，通过组合透明α混合阶段的图像，最终实现PBR混合。

2 预处理

预处理阶段的目的是将点划分为组，以实现以下两个目标：(1) 最小化单个组内splat之间的重叠，以便将PBR混合推迟到图像合成后处理阶段；(2) 每个组提供良好的表面覆盖，以允许透明α混合。最小重叠分组可以表述为K色加权图着色（WGC）问题。我们定义加权图\(G(S, E)\)，其中点集\(S = \{p_1...p_n\}\)，边集\(E = \{e_{ij} \vert \text{当且仅当} p_i \text{和} p_j \text{有非零重叠}\}\)，权重集\(W = \{w_{ij} \vert p_i \text{和} p_j \text{之间的重叠}\}\)。K色WGC的目标是为\(G\)中的每个节点分配一种颜色，生成K个子图，同时最小化子图中的权重和。该问题可以通过两步贪心策略解决，包括初始化和优化步骤。为了提高表面覆盖率，某些splat可能会在组之间重复，或者splat半径可以增大。

3 渲染

需要注意的是，PBR混合核不能用作插值权重，因为它们会干扰透明α混合。因此，每个片段对最终平滑点插值的贡献是相等的。由于以下观察，可以通过单独考虑最近的透明层来掩盖这种简化的PBR混合引入的视觉伪影：首先，视觉伪影在透明表面层后面显著减少；其次，在当前8位颜色和α分辨率下，任何低于1/256的误差都没有影响。因此，我们可以单独且高质量地渲染最近层，使用PBR混合核，因为同一层内没有α混合。以下3通道算法描述了我们透明PBR解决方案的基本方法：

1. 最近层的几何通道：使用高质量的PBR混合将WGC算法生成的点组\(S_k\)渲染到K个目标图像\(F_k\)中，包括最近片段的深度（深度缓冲Z）和混合核权重信息。

2. 其他层的几何通道：使用从后到前的透明α混合将点组\(S_k\)渲染到K个目标图像\(O_k\)中，但忽略来自最近层的所有片段，使用前一个通道的深度掩码Z。

3. 合成通道：根据每个片段的PBR核权重将图像\(F_k\)组合在一起，生成最近可见层的平滑插值图像\(C_F\)。将图像\(O_k\)平均为\(C_O\)。最终通过α合成\(C_F\)和\(C_O\)实现高质量的透明效果。

fig.1

图1：渲染结果。a) 不透明和透明对象；b) 折射和反射环境映射，包括菲涅尔效应和色散效果。

我们的方法允许混合不透明和透明点表面正确渲染，如图1 a)所示。需要注意的是，不透明表面和基本透明点渲染可以通过修改的算法实现，该算法仅对点几何进行一次渲染，此处不再进一步讨论，但在附带的视频中进行了演示。高质量的透明PBR如图1 b)所示。事实上，我们的算法还可以模拟多层折射和反射等视觉效果，也在视频序列中进行了演示。

评论