论文重点与难点

1 研究背景与挑战

• 透明物体重建的难点：透明物体由于折射和反射的特性，其光线路径复杂，难以通过传统方法进行几何重建。以往方法依赖于复杂设置（如手动标注、暗室条件或特殊图案），限制了其实际应用。

• 简化设置的需求：本文提出了一种在自然场景中仅使用多视角RGB图像重建透明物体的方法，无需手动标注或特殊环境设置，大大简化了透明物体重建的流程。

2 方法的核心技术

• 体积渲染与轮廓估计：

• 体积渲染：通过神经体积渲染（Neural Volume Rendering）技术，将整个场景（包括透明物体和背景平面）建模为一个3D神经场，忽略透明物体的折射和反射，将其视为具有自身颜色的不透明物体。虽然这种方法可以准确恢复背景平面的形状，但透明物体的形状会严重退化。

• 轮廓估计：通过分析体积渲染中光线的权重分布，将优化后的3D神经场投影回输入视图，估计透明物体的多视角轮廓。这些轮廓为后续的形状重建提供了强约束。

• 基于可微分折射渲染的形状重建：

• 神经SDF场：使用神经符号距离场（Neural SDF Field）表示透明物体的形状，避免了离散化误差。

• 可微分折射渲染：通过隐式折射渲染技术，优化透明物体的形状，使其折射出的颜色与输入图像一致。该方法考虑了折射路径的优化，而无需显式匹配光线与背景的对应关系。

• 光线采样：为了降低计算成本，仅对靠近轮廓边缘的光线进行采样，计算轮廓损失，而不是对所有光线进行计算。

3 实验验证

• 合成数据实验：

• 数据来源：使用Mitsuba渲染器生成合成数据，透明物体的形状来自在线资源和现有数据集，背景平面的纹理来自公开数据集。

• 结果：本文方法能够准确估计透明物体的多视角轮廓，并重建出高精度的形状。例如，对于“Dog”形状，使用108张输入图像时，轮廓误差为$6.1 \times 10^{-3}$，形状误差为$0.77 \times 10^{-5}$。

• 真实数据实验：

• 数据采集：使用普通RGB相机拍摄40-50张多视角图像，并通过COLMAP获取相机参数。

• 结果：与现有方法（如Li et al. 2020）相比，本文方法能够更准确地重建出透明物体的细节，如虎的腹部褶皱、牛的尾巴和角等。例如，对于“Cow”形状，本文方法的轮廓误差为$6.00 \times 10^{-3}$，形状误差为$0.25 \times 10^{-4}$，而Li et al. 2020方法的形状误差为$1.85 \times 10^{-4}$。

4 难点与解决方案

• 多段折射路径优化的病态性：透明物体的折射路径优化是一个高度病态的问题，需要额外的约束来收敛到真实情况。本文通过估计多视角轮廓为优化提供了强约束。

• 基于颜色的优化：直接基于颜色监督优化折射路径可能会导致歧义和高频伪影。本文通过神经SDF场的隐式表示和可微分渲染技术，避免了这些问题。

• 计算成本：优化过程中需要计算大量的光线与形状的交互。本文通过采样靠近轮廓边缘的光线来降低计算成本。

5 局限性与未来工作

• 接触区域的重建问题：对于透明物体与背景平面接触的区域（如物体的脚部），由于这些区域的折射畸变较少，难以通过当前方法准确重建。

• 未来改进方向：可能需要进一步优化折射渲染模型，或者引入额外的约束条件来改善接触区域的重建效果。

论文详细讲解

1 研究背景与动机

透明物体的几何重建一直是计算机视觉中的一个难题。其主要挑战在于透明物体的折射和反射特性导致光线路径复杂，难以通过传统方法进行精确重建。以往的方法通常依赖于复杂的设置，例如手动标注物体轮廓、在暗室条件下拍摄，或者使用带有特殊图案的背景来推断光线与背景的对应关系。这些方法虽然能够取得一定的效果，但设置复杂，限制了其在普通用户中的应用。

本文提出了一种在自然场景中仅使用多视角RGB图像重建透明物体的方法，无需手动标注或特殊环境设置，大大简化了透明物体重建的流程。

2 方法概述

本文的核心思想是利用神经体积渲染和可微分折射渲染来重建透明物体的几何形状。具体来说，方法分为以下几个关键步骤：

1. 场景重建与轮廓估计：

• 使用神经体积渲染技术将整个场景（包括透明物体和背景平面）建模为一个3D神经场。

• 通过分析体积渲染中光线的权重分布，将优化后的3D神经场投影回输入视图，估计透明物体的多视角轮廓。

• 这些轮廓为后续的形状重建提供了强约束。

2. 基于可微分折射渲染的形状重建：

• 使用神经符号距离场（Neural SDF Field）表示透明物体的形状，避免了离散化误差。

• 通过隐式折射渲染技术，优化透明物体的形状，使其折射出的颜色与输入图像一致。

• 采用光线采样方法，仅对靠近轮廓边缘的光线进行采样，计算轮廓损失，降低计算成本。

3 场景重建与轮廓估计

3.1 神经体积渲染

• 场景网络：使用场景网络$A_{scene}$来表示整个场景的形状和外观，其中$A_{scene} : (x, v) \rightarrow (d, c)$，$x$是3D位置，$v$是视图方向，$d$是符号距离，$c$是颜色。

• 体积渲染：通过神经体积渲染技术优化$A_{scene}$，恢复场景的外观和形状。然而，由于透明物体的外观随视图方向变化较大，体积渲染无法准确恢复透明物体的形状，但可以准确恢复背景平面的形状。

3.2 轮廓估计

• 权重分布分析：对于射向背景平面的光线和射向透明物体的光线，其权重分布存在显著差异。通过分析这些权重分布，可以估计出透明物体的轮廓。

• 轮廓函数：定义轮廓函数$S(x, v)$，通过积分光线上的权重来判断光线是否击中透明物体。对于射向背景平面的光线，$S(x, v) = 0$；对于射向透明物体的光线，$S(x, v) = 1$。通过设置阈值（如0.4），可以确定每条光线是否击中透明物体，从而估计出多视角的轮廓。

4 基于可微分折射渲染的形状重建

4.1 神经SDF场

• 对象网络：使用对象网络$A_{obj}$来表示透明物体的SDF场，仅输出SDF值以专注于形状重建。

• 轮廓损失：使用估计的轮廓对$A_{obj}$进行初始化，并添加Eikonal正则化项以约束SDF场的梯度。

4.2 可微分折射渲染

• 隐式折射渲染：对于每条光线，通过SDF场找到与透明物体表面的交点，并根据斯涅尔定律计算折射光线。忽略反射光线，因为它们通常不会击中背景平面。

• 渲染过程：通过两次折射计算最终的渲染颜色。具体来说，对于一条光线，首先找到与透明物体表面的交点，计算折射光线，然后再次折射以获取最终的渲染颜色。渲染颜色通过背景平面的纹理获取。

• Fresnel项：计算两次折射的Fresnel项，以考虑光线在界面处的反射损失。

4.3 光线采样

• 轮廓约束：为了降低计算成本，仅对靠近轮廓边缘的光线进行采样，计算轮廓损失。通过形态学梯度（如膨胀和腐蚀操作）选择靠近轮廓边缘的光线。

5 实验验证

5.1 合成数据实验

• 数据生成：使用Mitsuba渲染器生成合成数据，透明物体的形状来自在线资源和现有数据集，背景平面的纹理来自公开数据集。

• 结果：本文方法能够准确估计透明物体的多视角轮廓，并重建出高精度的形状。例如，对于“Dog”形状，使用108张输入图像时，轮廓误差为$6.1 \times 10^{-3}$，形状误差为$0.77 \times 10^{-5}$。

5.2 真实数据实验

• 数据采集：使用普通RGB相机拍摄40-50张多视角图像，并通过COLMAP获取相机参数。

• 结果：与现有方法（如Li et al. 2020）相比，本文方法能够更准确地重建出透明物体的细节，如虎的腹部褶皱、牛的尾巴和角等。例如，对于“Cow”形状，本文方法的轮廓误差为$6.00 \times 10^{-3}$，形状误差为$0.25 \times 10^{-4}$，而Li et al. 2020方法的形状误差为$1.85 \times 10^{-4}$。

6 局限性与未来工作

• 接触区域的重建问题：对于透明物体与背景平面接触的区域（如物体的脚部），由于这些区域的折射畸变较少，难以通过当前方法准确重建。

• 未来改进方向：可能需要进一步优化折射渲染模型，或者引入额外的约束条件来改善接触区域的重建效果。

详细讲解论文的方法部分

1 方法概述

本文提出了一种基于隐式可微分折射渲染的方法，用于从多视角RGB图像重建自然场景中的透明物体。该方法的核心在于两个关键技术：

• 体积渲染与轮廓估计：通过体积渲染估计透明物体的多视角轮廓。

• 可微分折射渲染：利用神经符号距离场（SDF）进行可微分折射渲染，优化透明物体的形状，使其折射出的颜色与输入图像一致。

2 体积渲染与轮廓估计

2.1 体积渲染

• 场景网络：使用神经网络$A_{scene}$表示整个场景的形状和外观，其中$A_{scene} : (x, v) \rightarrow (d, c)$，$x$是3D位置，$v$是视图方向，$d$是符号距离，$c$是颜色。

• 优化过程：通过神经体积渲染优化$A_{scene}$，恢复场景的外观和形状。具体来说，体积渲染通过积分光线上的颜色信息来计算最终像素颜色：

$$C(r) = \int_{0}^{+\infty} L(x) \cdot T(x) \cdot \alpha(x) \, dx$$

其中，$L(x)$是点$x$的颜色，$T(x)$是光线从起点到点$x$的透射率，$\alpha(x)$是点$x$的不透明度。

2.2 轮廓估计

• 权重分布分析：对于射向背景平面的光线和射向透明物体的光线，其权重分布存在显著差异。通过分析这些权重分布，可以估计出透明物体的轮廓。

• 轮廓函数：定义轮廓函数$S(x, v)$，通过积分光线上的权重来判断光线是否击中透明物体：

$$S(x, v) = \int_{0}^{+\infty} \alpha(x) \, dx$$

对于射向背景平面的光线，$S(x, v) \approx 0$；对于射向透明物体的光线，$S(x, v) \approx 1$。通过设置阈值（如0.4），可以确定每条光线是否击中透明物体，从而估计出多视角的轮廓。

3 基于可微分折射渲染的形状重建

3.1 神经SDF场

• 对象网络：使用对象网络$A_{obj}$来表示透明物体的SDF场，仅输出SDF值以专注于形状重建。$A_{obj} : x \rightarrow d$，其中$d$是符号距离。

• 轮廓损失：使用估计的轮廓对$A_{obj}$进行初始化，并添加Eikonal正则化项以约束SDF场的梯度：

$$\mathcal{L}_{eikonal} = \left\| \nabla A_{obj}(x) - 1 \right\|_2$$

3.2 可微分折射渲染

• 隐式折射渲染：对于每条光线，通过SDF场找到与透明物体表面的交点，并根据斯涅尔定律计算折射光线。忽略反射光线，因为它们通常不会击中背景平面。

• 渲染过程：通过两次折射计算最终的渲染颜色。具体来说，对于一条光线，首先找到与透明物体表面的交点，计算折射光线，然后再次折射以获取最终的渲染颜色：

$$C_{rendered} = (1 - F_1)(1 - F_2) \cdot C_{background}$$

其中，$F_1$和$F_2$是两次折射的Fresnel项，$C_{background}$是背景平面的颜色。

• Fresnel项：计算两次折射的Fresnel项，以考虑光线在界面处的反射损失：

$$F = \frac{1}{2} \left( \frac{\eta_1 \cos \theta_i - \eta_2 \cos \theta_t}{\eta_1 \cos \theta_i + \eta_2 \cos \theta_t} \right)^2 + \frac{1}{2} \left( \frac{\eta_2 \cos \theta_t - \eta_1 \cos \theta_i}{\eta_2 \cos \theta_t + \eta_1 \cos \theta_i} \right)^2$$

其中，$\eta_1$和$\eta_2$分别是入射介质和折射介质的折射率，$\theta_i$和$\theta_t$分别是入射角和折射角。

3.3 光线采样

• 轮廓约束：为了降低计算成本，仅对靠近轮廓边缘的光线进行采样，计算轮廓损失。通过形态学梯度（如膨胀和腐蚀操作）选择靠近轮廓边缘的光线：

$$S_{sampled} = S \oplus k - S \ominus k$$

其中，$k$是结构元素（如5×5的方形核），$\oplus$和$\ominus$分别表示膨胀和腐蚀操作。

4 优化目标

• 渲染损失：衡量渲染颜色与输入图像颜色的差异：

$$\mathcal{L}_{render} = \frac{1}{|R|} \sum_{r \in R} \left\| C_{rendered}(r) - C_{input}(r) \right\|_1$$

其中，$R$是采样光线集合，$C_{rendered}(r)$是渲染颜色，$C_{input}(r)$是输入图像颜色。

• 轮廓损失：提供额外的约束，防止退化结果：

$$\mathcal{L}_{silhouette} = \frac{1}{|S_{sampled}|} \sum_{r \in S_{sampled}} \left\| S_{estimated}(r) - S_{groundtruth}(r) \right\|_1$$

• 正则化损失：添加Eikonal正则化项以约束SDF场的梯度：

$$\mathcal{L}_{regularization} = \left\| \nabla A_{obj}(x) - 1 \right\|_2$$

• 总损失：

$$\mathcal{L} = \lambda_1 \mathcal{L}_{render} + \lambda_2 \mathcal{L}_{silhouette} + \lambda_3 \mathcal{L}_{regularization}$$

其中，$\lambda_1, \lambda_2, \lambda_3$是权重系数。

5 实验验证

• 合成数据实验：使用Mitsuba渲染器生成合成数据，透明物体的形状来自在线资源和现有数据集，背景平面的纹理来自公开数据集。实验结果表明，本文方法能够准确估计透明物体的多视角轮廓，并重建出高精度的形状。

• 真实数据实验：使用普通RGB相机拍摄40-50张多视角图像，并通过COLMAP获取相机参数。实验结果表明，本文方法能够更准确地重建出透明物体的细节，如虎的腹部褶皱、牛的尾巴和角等。

6 局限性与未来工作

• 接触区域的重建问题：对于透明物体与背景平面接触的区域（如物体的脚部），由于这些区域的折射畸变较少，难以通过当前方法准确重建。

• 未来改进方向：可能需要进一步优化折射渲染模型，或者引入额外的约束条件来改善接触区域的重建效果。

原文翻译

通过隐式可微折射渲染实现透明物体重建

作者：

Fangzhou Gao∗ 天津大学 中国 gaofangzhou@tju.edu.cn

Lianghao Zhang∗ 天津大学 中国 opoiiuiouiuy@tju.edu.cn

Li Wang 天津大学 中国 li_wang@tju.edu.cn

Jiamin Cheng 天津大学 中国 cjm@tju.edu.cn

Jiawan Zhang† 天津大学 中国 jwzhang@tju.edu.cn

摘要

重建透明物体的几何形状一直是一个长期存在的挑战。现有方法依赖于复杂的设置，例如手动标注或暗室条件，以获取物体轮廓，并且通常需要具有设计图案的受控环境来推断射线与背景的对应关系。然而，这些复杂的安排限制了普通用户的实际应用。在本文中，我们显著简化了设置，并提出了一种在未知自然场景中无需人工辅助即可重建透明物体的新方法。我们的方法结合了两项关键技术。首先，我们引入了一种基于体渲染的方法，通过将3D神经场投影到2D图像上来估计物体轮廓。这一自动化过程从自然场景中捕获的图像中生成高度准确的多视角物体轮廓。其次，我们提出了通过可微折射渲染与神经SDF场进行透明物体优化的方法，使我们能够基于颜色而非显式的射线-背景对应关系来优化折射射线。此外，我们的优化还包括一种射线采样方法，以低计算成本监督物体轮廓。大量的实验和比较表明，我们的方法在提供更便捷设置的同时，能够生成高质量的结果。

CCS概念

• 计算方法 → 重建；网格几何模型。

关键词

透明物体，多视角重建，神经渲染

ACM参考格式

Fangzhou Gao, Lianghao Zhang, Li Wang, Jiamin Cheng, and Jiawan Zhang. 2023. 通过隐式可微折射渲染实现透明物体重建。在SIGGRAPH Asia 2023会议论文（SA会议论文’23），2023年12月12-15日，悉尼，新南威尔士州，澳大利亚。ACM，纽约，纽约州，美国，11页。https://doi.org/10.1145/3610548.3618236

1 引言

透明物体由于折射和反射所表现出的独特特性，给其重建带来了长期挑战。由多段组成的复杂光路阻碍了大多数常用方法中使用的对应匹配。在重建透明物体时，必须考虑物体的环境，以分析和约束折射光路。先前的方法要么将环境建模为已知的环境光照以输入预训练网络[Li et al. 2020]，要么需要独特的图案来推断相机射线与背景之间的对应关系[Lyu et al. 2020; Wu et al. 2018; Xu et al. 2022]。然而，这些严格的前提条件在实践中导致了复杂的设置，例如提前捕获环境图或部署显示设计图案的显示器。此外，它们都依赖于手动标注[Li et al. 2020; Xu et al. 2022]或暗室[Lyu et al. 2020; Wu et al. 2018]来提取多视角物体轮廓。这种复杂的设置给普通用户带来了沉重的负担，并限制了实际应用。但由于两个问题，简化设置具有挑战性。首先，优化多段折射光路是一个严重不适定问题[Kutulakos and Steger 2008]，它严重依赖于物体轮廓来提供额外的约束。然而，简单的基于图像的分割方法很难估计出跨视角一致的准确轮廓。其次，虽然基于颜色而非显式的射线-背景对应关系来优化折射射线是一种有前景的方法，但监督颜色会加剧歧义，并导致自交、折叠和显式网格表示中的高频伪影，即使是最近的混合表示[Xu et al. 2022]。在本文中，我们解决了这两个问题，并提出了一种新方法，能够从多视角RGB图像中自动重建未受控自然场景中的透明物体。我们的方法显著简化了透明物体重建所需的设置，使其与用于不透明物体的多视角立体方法一样便捷。这一成果归功于两项关键技术的结合。首先，我们观察并分析了使用神经体渲染进行透明物体重建时产生的形状-辐射度歧义。虽然通过体渲染得到的透明物体形状仍然不准确，但我们提出将3D神经场投影回每个输入视图，并判断射线是否击中透明物体。通过投影，轮廓中的正样本可以通过不完美的透明表面恢复，而负样本则通过恢复良好的不透明环境恢复。这些多视角轮廓为后续物体重建提供了强有力的正则化。其次，我们利用输入图像和估计的轮廓来重建透明物体，表示为神经SDF场。神经隐式表示避免了优化过程中的离散化伪影。重建主要依赖于神经SDF场的隐式可微折射渲染。这种方法使我们能够通过强制重建物体折射出与输入图像相同的颜色来优化折射光路和物体形状，使其接近真实情况。此外，重建还包括一种射线采样方法，以低计算成本选择最重要的射线来约束物体轮廓。总之，据我们所知，我们提出了第一种仅使用多视角RGB照片作为输入，在未受控自然场景中重建透明物体的方法。它极大地简化了透明物体重建的设置，这归功于以下技术贡献：

• 从3D神经场估计准确的多视角2D物体轮廓的投影方法。

• 通过神经SDF场的可微折射渲染进行透明物体优化。

• 用于低成本轮廓约束的射线采样。

在合成数据和真实数据上进行的实验评估验证了我们提出方法的优越性。我们的方法在更便捷的设置下，取得了比先前方法更好的结果。

2 相关工作

在本节中，我们回顾了关于透明表面重建的研究。此外，我们简要回顾了通过神经渲染对不透明物体进行的多视图重建，这启发我们将神经渲染应用于透明物体的重建。

2.1 透明表面重建

由于透明表面独特的光学特性，重建透明表面具有挑战性。为此，引入了各种特殊的硬件和设置，例如光场探针[Wetzstein et al. 2011]、偏振相机[Huynh et al. 2010; Miyazaki and Ikeuchi 2005]、深度相机[Alt et al. 2013; Tanaka et al. 2016]和断层扫描[Trifonov et al. 2006]。更多细节可以在综述[Ihrke et al. 2010]中找到。此外，还提出了一系列使用消费级相机重建透明表面的方法，这些方法可以分为在受控环境中的重建和在自然场景中的重建。

2.1.1 受控环境

Kutulakos等人[2008]分析了透明表面的光路三角测量。基于此，一系列方法被提出，用于重建单层[Morris and Kutulakos 2011; Qian et al. 2017; Shan et al. 2012]和双层透明表面[Qian et al. 2016]，通过在环境中使用特殊图案来提供相机光线与环境点之间的对应关系。Wu等人[2018]提出了一种方法，通过在暗室中使用转台和显示格雷码的显示器来重建透明物体的完整3D形状。这种设置使他们能够获得多视角的对应关系。从视觉外壳开始，通过强制其法线将光线折射到正确的方向来优化物体的点云。Lyu等人[2020]进一步改进了该方法，使用基于网格的可微分折射光线追踪，恢复了更详细的形状。最近，提出了一种混合网格-神经表示方法，用于在自然光下恢复详细形状，并使用iPad显示设计的图案[Xu et al. 2022]。除了分析折射外，一些方法还利用透明表面的镜面反射与受控光源[Morris and Kutulakos 2007; Yeung et al. 2011]。与这些方法相比，我们的方法可以在不受控制的自然场景中重建透明物体。

2.1.2 自然场景

Morris等人[2014]和Xiong等人[2021]重建了流体表面和浸入场景。Stets等人[2019]使用深度学习从单张图像中预测透明物体的深度和法线。此外，一些基于神经网络的方法被提出，用于恢复透明表面的深度图，以用于机器人操作[Ichnowski et al. 2021; Sajjan et al. 2020; Zhu et al. 2021]。Li等人[2020]引入了一种基于物理的网络，用于在自然光照条件下重建透明物体的完整形状。他们在潜在特征空间中优化了物体形状。然而，他们的方法依赖于预先捕获的环境图和手动注释的多视角轮廓。相比之下，我们的方法消除了预先获取和手动注释的需求，使其更加方便和实用。此外，最近提出了一种折射新视角合成方法[Bemana et al. 2022]。但它旨在进行视角合成，无法为复杂的透明物体生成真实的形状。更多讨论见第4节。

2.2 基于神经渲染的多视角重建

最近，一系列基于可微分渲染的方法被提出，用于恢复不透明物体的形状和外观，并将其表示为隐式神经场，从而能够以较低的成本连续恢复3D内容。根据渲染技术的不同，这些方法可以分为基于表面渲染和基于体渲染的方法。基于表面渲染的方法根据光线与物体表面的交点确定辐射度，这种方法只能将梯度反向传播到局部区域，并且需要物体掩码作为监督[Niemeyer et al. 2020; Yariv et al. 2020]。相比之下，NeRF [Mildenhall et al. 2020] 及其后续工作[Darmon et al. 2022; Fu et al. 2022; Oechsle et al. 2021; Wang et al. 2021; Yariv et al. 2021] 使用体渲染来聚合沿光线所有采样点的辐射度。这些方法能够收敛到更好的结果，并且不需要掩码。受这些方法的启发，我们将神经渲染应用于折射，并从多视角图像中重建透明物体。

3 方法

3.1 概述

为了从RGB图像中重建透明物体，我们假设环境具有丰富的纹理，从而产生明显的折射畸变作为视觉线索。我们采用可微折射渲染来在未知的自然场景中重建透明物体。然而，直接通过折射恢复物体的形状极具挑战性。一方面，周围环境未知，这阻碍了折射渲染。另一方面，优化多分段折射光路是一个高度不适定的问题，如果没有额外的约束，无法收敛到真实情况。

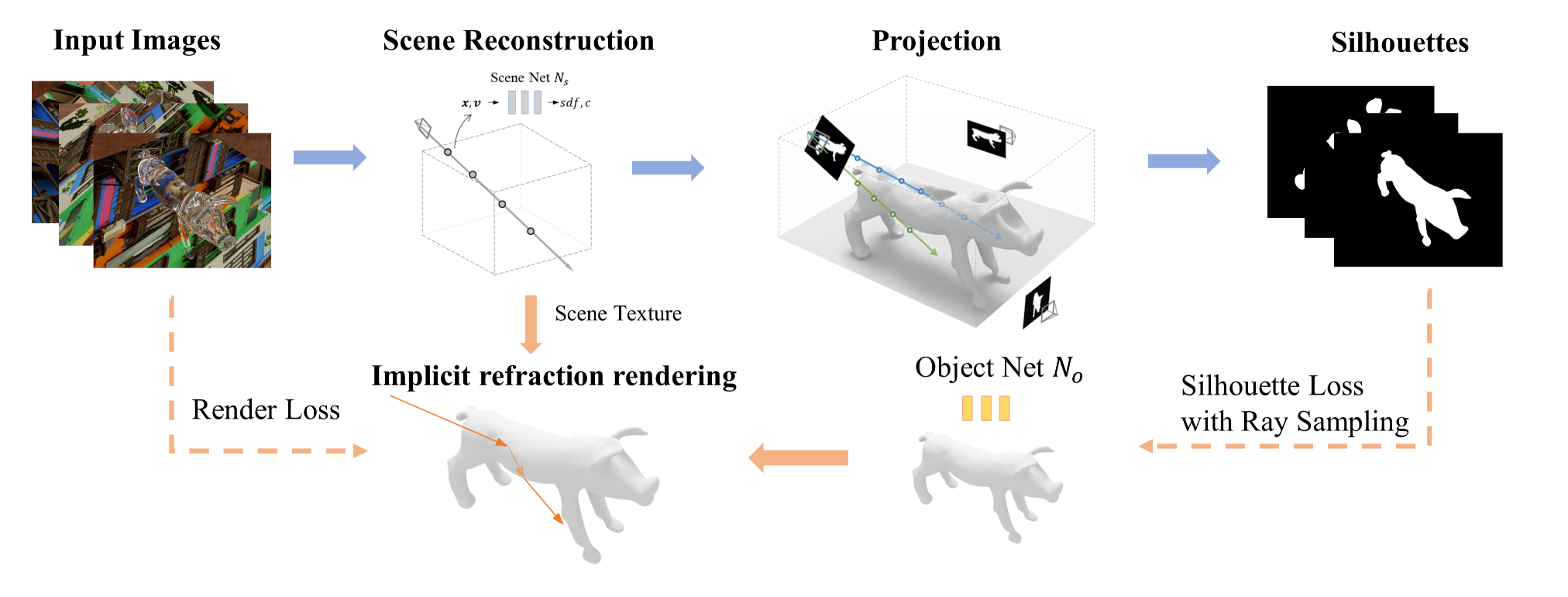
图2：我们方法的概述。我们首先采用神经体渲染来恢复整个场景，并通过将神经场投影回输入视图来估计物体轮廓。然后，我们通过隐式折射渲染重建物体的形状，使其折射出与输入图像相同的颜色。我们还利用估计的轮廓，通过设计的射线采样方法对物体形状进行正则化。

因此，我们首先忽略折射和反射，将透明物体的外观视为其自身的固有颜色，与不透明的周围环境采用相同的外观模型。假设透明物体放置在一个外观未知的平面上，我们使用神经网络$N_s$来表示整个场景的形状和外观，包括透明物体和平面。随后，我们通过神经体渲染对网络$N_s$进行优化，由于多视图图像施加的约束，这可以准确恢复不透明平面的外观和形状。对于透明物体，如图2上部所示，我们舍弃其不准确的深度信息，并将优化后的神经场投影回输入视图，以获取准确的多视图物体轮廓。这些轮廓在后续阶段作为物体重建的强约束条件。

图2：我们方法的概述。我们首先采用神经体渲染来恢复整个场景，并通过将神经场投影回输入视图来估计物体轮廓。然后，我们通过隐式折射渲染重建物体的形状，使其折射出与输入图像相同的颜色。我们还利用估计的轮廓，通过设计的射线采样方法对物体形状进行正则化。

利用恢复的平面和轮廓，我们接着考虑实际的折射过程，并重建出与输入图像颜色相同的折射物体。为了实现这一点，我们使用一个称为$N_o$的新物体网络来拟合物体的有符号距离场（SDF）。神经隐式表示是连续的，并且没有离散化伪影[Niemeyer等人，2020]。用估计的轮廓初始化网络$N_o$后，如图2下部所示，我们随后通过具有神经SDF场的可微折射渲染和渲染损失来优化$N_o$。物体的形状和折射光路被优化到真实情况，以便折射出与输入相同的颜色。在优化过程中，我们仅对靠近轮廓边缘的光线计算轮廓损失，以此来约束物体轮廓，有效降低了计算成本。

在本文的其余部分，我们首先描述透明物体重建前的准备工作，包括场景重建和物体轮廓估计（3.2节），然后详细介绍物体重建（3.3节）。

3.2 场景重建和轮廓估计

在这一步中，我们忽略折射，假设光线沿直线传播。我们使用场景网络$N_s$来表示整个场景的形状和外观。通过位置编码，$N_s : (x, v) \to s, c$将三维位置$x$映射为与视角无关的有符号距离$s$和与视角相关的颜色$c$。随后，我们采用[Wang等人，2021]中的神经体渲染方法来优化$N_s$。

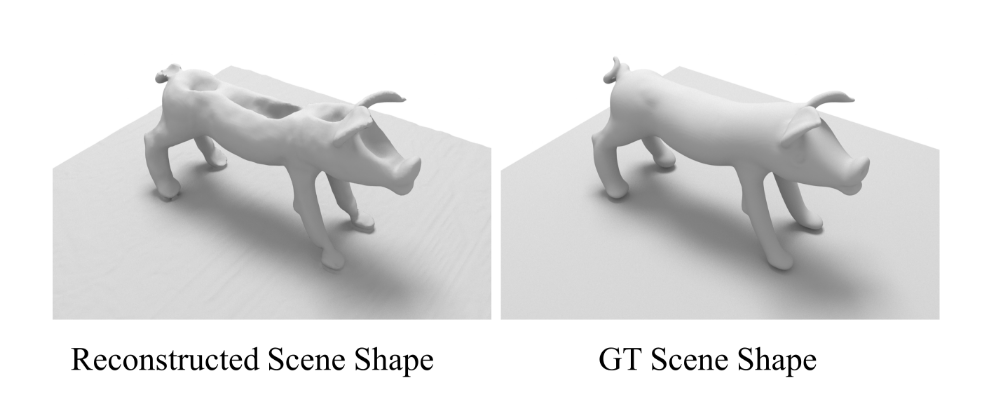
图3：通过神经体渲染优化的场景形状。场景由一个不透明平面和一个放置在其上的透明物体组成。前者被很好地恢复，而后者则退化。

然而，仅靠这种方法无法得到精确的几何形状。虽然不透明平面能得到较好的重建，但如图3所示，透明物体的形状严重失真。这主要是因为透明物体的“自身外观”会随视角方向快速变化，不完全符合神经体渲染中平滑的双向反射分布函数（BRDF）假设[Zhang等人，2020]。因此，出现了形状 - 辐射度模糊问题。

尽管在形状重建中存在固有误差，我们对光线的权重分布进行了分析，并利用它来估计精确的物体轮廓。

在体渲染中，对于表示为$p(t) = o + tv$的光线，其颜色计算如下：

$$C = \int_{0}^{+\infty} w(t)c(t)dt \tag{1}$$

其中，$w(t)$是点的权重，在我们的方法中，它如[Wang等人，2021]所述，根据有符号距离场（SDF）值计算得出。

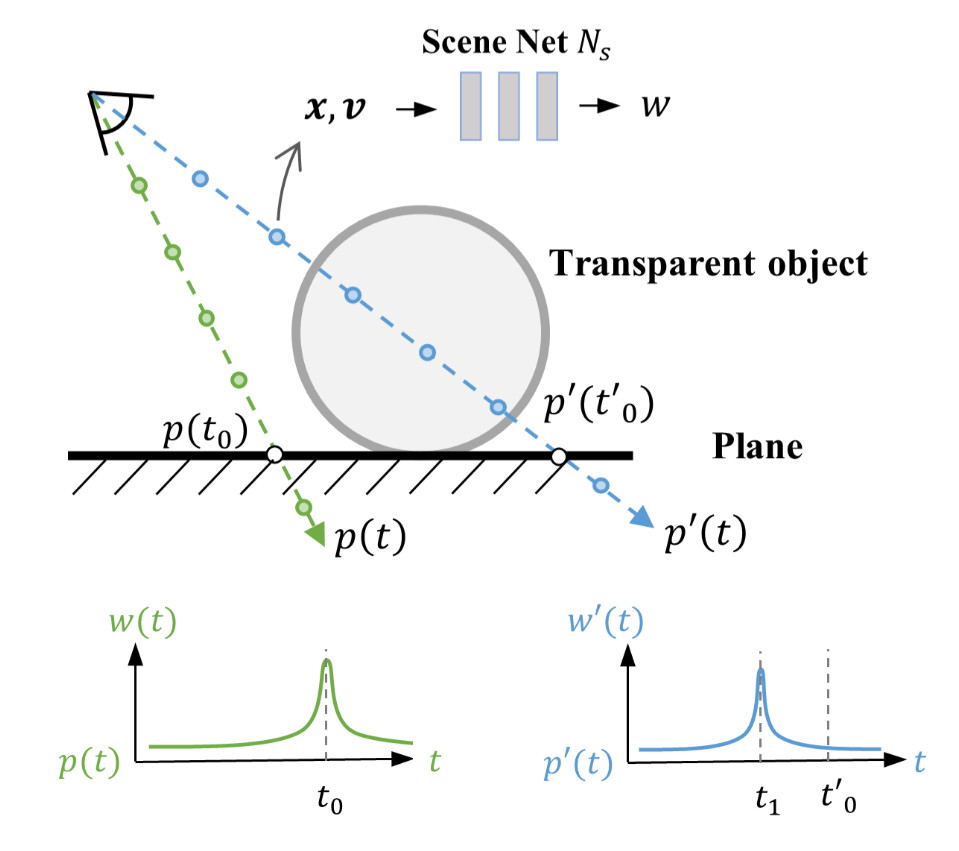
图4：射线$p(t)$和射线$p’(t)$的权重分布示意图。$p(t_0)$和$p’(t’_0)$分别是它们与平面的交点。我们在下方展示了权重分布。

在我们的场景中，透明物体放置在不透明平面上，存在两种光线：击中平面的光线和击中透明物体的光线，如图4所示。对于击中平面的光线$p(t)$，由于平面是具有平滑双向反射分布函数（BRDF）的简单不透明物体，它应该能很好地收敛到接近真实的情况。该光线的颜色应该仅由平面上交点的颜色决定。设$t_0$表示光线与平面交点的深度，大致上，我们有：

$$w(t)= \begin{cases} 0, & t \neq t_0 \\ 1, & t = t_0 \end{cases}\tag{2}$$

对于击中透明物体的光线$p’(t)$，由于折射和反射，其颜色与它和平面的交点$p’(t_0’)$的颜色有显著差异。因此，它必须由平面前方某点的颜色来拟合，大致可以表示为：

$$\exists t_1 < t_0',\quad w(t_1)=1\tag{3}$$

请注意，$t_1$通常不是透明表面的准确深度，因为正如我们前面提到的，其外观变化很快。

然后我们定义一个轮廓函数$f_M(o, v)$来计算沿光线的权重积分，同时将平面上及平面以下的点的权重手动设置为零。

$$\begin{align} f_M(o, v) &= \int_{0}^{+\infty} w'(t)dt \\ w'(t) &= \begin{cases} w(t), & t < t_0(\mathbf{o}, \mathbf{v}) \\ 0, & t \geq t_0(\mathbf{o}, \mathbf{v}) \end{cases} \end{align}\tag{4}$$

其中，$t_0(\mathbf{o}, \mathbf{v})$根据光线原点$\mathbf{o}$和方向$\mathbf{v}$计算光线与平面交点的深度。

图2：我们方法的概述。我们首先采用神经体渲染来恢复整个场景，并通过将神经场投影回输入视图来估计物体轮廓。然后，我们通过隐式折射渲染重建物体的形状，使其折射出与输入图像相同的颜色。我们还利用估计的轮廓，通过设计的射线采样方法对物体形状进行正则化。

可以很容易地算出，对于击中平面的光线，$f_M = 0$；对于击中物体的光线，$f_M = 1$。通过设置阈值$\sigma$，我们可以利用$f_M$来判断光线是否击中物体。阈值的选择对结果没有显著影响。在我们的实验中，阈值设为0.4。将$f_M$应用于所有光线，就能确定每个像素，进而估计出准确的多视图轮廓，如图2上部所示。对于每个视图，我们选择面积最大的连通区域作为最终结果，以消除噪声。这些估计出的轮廓为后续的形状重建提供了强有力的约束。

3.3 形状重建

我们使用一个新的物体网络$N_o$来表示透明物体的有符号距离场（SDF）。与场景网络$N_s$不同，$N_o$只输出SDF值，因为我们关注的是形状。我们采用[Wang等人，2021]中的轮廓损失，利用估计的轮廓来优化$N_o$，并添加[Gropp等人，2020]中的程函项作为正则化项。

仅由轮廓约束的初始形状不够准确。因此，我们进一步考虑实际的折射光路，并通过强制其折射颜色与输入图像一致来优化初始形状。这种监督主要通过隐式折射渲染和用于轮廓约束的光线采样来实现。

3.3.1 隐式折射渲染

为了使用SDF场对折射颜色进行可微渲染，对于图像中的一个像素，我们跟踪并折射光线，直到它击中平面以获取渲染颜色。我们仅考虑两次折射，不考虑反射，因为大多数反射光线不会击中平面。

具体来说，对于表示为$p(t) = o + tv$的光线，我们获取沿光线的一组采样点的SDF值，然后使用[Fu等人，2022]中的线性插值来定位光线与物体表面的交点$\hat{x}$。我们使用$\hat{x}$处的SDF梯度作为其法向量[Niemeyer等人，2020]：

$$n(\hat{x}) = \nabla S_{obj}(\hat{x}, v)/\|\nabla S_{obj}(\hat{x}, v)\|_2 \tag{5}$$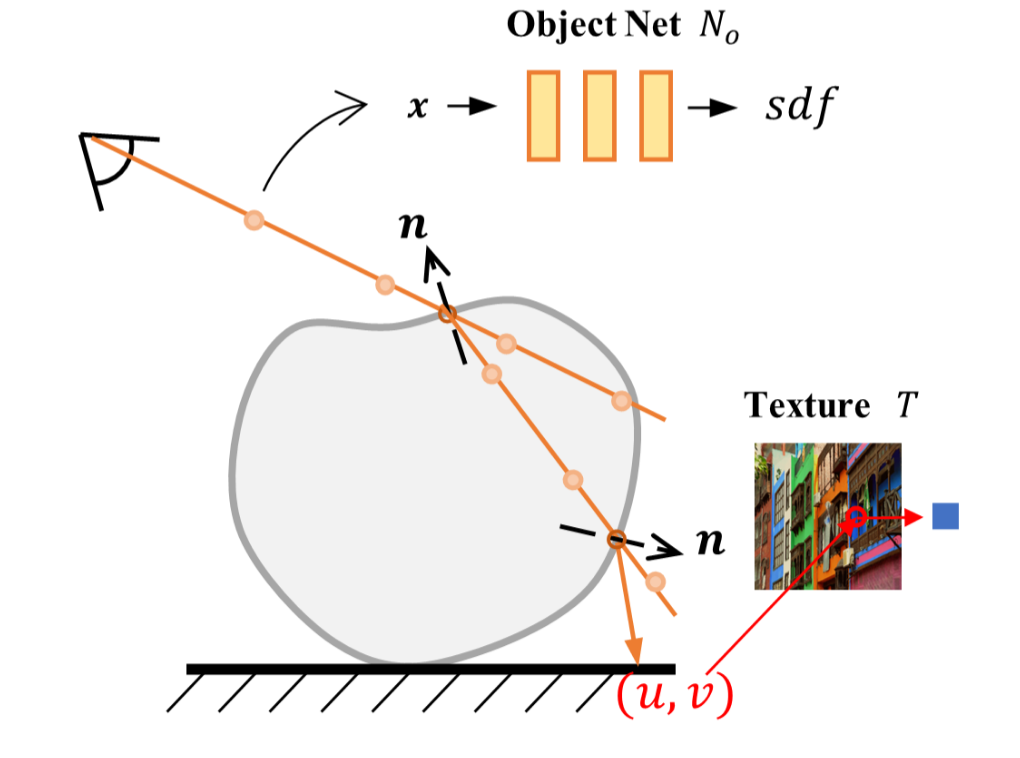

图5：我们的隐式折射渲染示意图。我们从采样点中定位射线与隐式SDF场的交点，并对其进行两次折射，直到它击中平面，从平面纹理中获取渲染颜色。

然后，根据斯涅尔定律和物体的折射率（IoR）计算折射光线，物体的初始折射率手动初始化为$IoR_{init}$，并与物体网络$N_o$一起进行优化。我们再次跟踪并折射新光线，以得到从物体射出的光线，该光线用于渲染最终颜色，如图5所示。

在光线跟踪过程中，两次折射的菲涅尔项$F_1$，$F_2$根据菲涅尔方程分别计算：

$$\mathcal{F} = \frac{1}{2}\left(\frac{\eta_i l_i \cdot n - \eta_t l_t \cdot N}{\eta_i l_i \cdot n + \eta_t l_t \cdot N}\right)^2 + \frac{1}{2}\left(\frac{\eta_t l_t \cdot N - \eta_i l_i \cdot n}{\eta_t l_t \cdot N + \eta_i l_i \cdot n}\right)^2 \tag{6}$$

其中，$\eta_i$，$\eta_t$分别是入射介质和折射介质的折射率。$l_i$，$l_t$分别是入射光线和折射光线的方向。

我们通过体渲染，从平面正上方分别渲染平面上的每个点。

为了渲染最终颜色，我们使用场景网络$N_c$，通过体渲染从顶视图渲染平面的外观。对于每个点，光线原点设置在其正上方非常近的位置，以排除透明物体的颜色。我们将渲染结果存储为与视角无关的显式纹理$T^*$，为了进行从粗到细的优化，该纹理可以进行模糊处理。在优化过程中，用于渲染的纹理$T$按如下方式进行模糊：

$$T = Gaussian(T^*, \sigma) \tag{7}$$

其中，$Gaussian$是高斯模糊，$\sigma$是模糊核的标准差，随着优化进行而减小。在我们的实验中，我们将纹理大小设置为$512×512$。

然后对于从物体射出的光线，我们计算它与平面的交点，并使用双线性插值获取纹理作为背景颜色$c_b$。渲染颜色$c$进一步计算为：

$$c = (1 - \mathcal{F}_1)(1 - \mathcal{F}_2)c_b \tag{8}$$

虽然我们的方法可以处理未知且任意的平面纹理，只要它们能产生明显的折射畸变，但纹理丰富的平面可以减少颜色模糊性，有助于光线收敛，并得到更准确的结果。

3.3.2 用于轮廓约束的光线采样

我们继续使用估计的轮廓来约束物体的形状。然而，计算所有光线的轮廓损失效率很低。由于最终的形状接近较好的初始状态，在整个优化过程中，大多数远离轮廓边缘的光线的轮廓损失都很低。并且神经SDF的权重只能沿着光线进行优化[Zhang等人，2022]。因此，这些光线无法有效地监督物体的形状。

我们不计算所有光线的轮廓损失，而是对靠近轮廓边缘的光线进行采样，这些光线对于约束轮廓最为重要，然后计算轮廓损失。这使我们能够大幅减少用于计算轮廓损失的光线数量。在我们的实验中，通过形态学梯度很容易实现这一点：

$$G_i = M_i \oplus b - M_i \ominus b \tag{9}$$

其中，$M_i$是第$i$个轮廓，$b$是一个结构元素，在我们的实验中是一个$5×5$的方形核，$\oplus$和$\ominus$分别表示膨胀和腐蚀操作，$G_i$是采样结果。在优化过程中，我们仅使用$G_i$内的光线来计算轮廓损失。

3.3.3 损失

我们使用以下损失来优化物体网络$S_o$和折射率：

$$L = \lambda_{ren}L_{render} + \lambda_{sil}L_{silhouette} + \lambda_{reg}L_{regularize} \tag{10}$$

其中，$L_{render}$是渲染损失，$L_{silhouette}$是轮廓损失，$L_{regularize}$是正则化损失。$\lambda_{ren}$、$\lambda_{sil}$、$\lambda_{reg}$分别为1.0、1.0、1.5。

• 渲染损失：渲染损失衡量渲染颜色与输入图像中真实颜色之间的差异。对于每次迭代，我们在估计的轮廓内对光线进行采样以计算渲染损失。在隐式折射渲染过程中，能够在不发生全反射的情况下击中平面的有效光线被记录为二值掩码$M_{ren}$。将光线$p$的像素颜色记为$\widetilde{c}(p)$，渲染颜色记为$c(p)$，渲染损失计算如下：

$$L_{render} = \frac{1}{|M_{ren}|} \sum_{p} M_{ren}(p)\|c(p) - \widetilde{c}(p)\|_1 \tag{11}$$

• 轮廓损失：轮廓损失为优化提供了额外的约束，并有效地防止结果退化。与用于计算渲染损失的采样光线无关，对于每次迭代，我们在$G_i$内对光线进行采样，以计算与形状初始化时相同的轮廓损失。

• 正则化损失：我们对用于计算渲染损失和轮廓损失的光线都计算[Gropp等人，2020]中的程函项，以对SDF场进行正则化。我们还添加权重为0.1的$l_2$损失$|IoR - IoR_{init}|_2$来对折射率进行正则化。

4 实验

我们在合成数据和真实数据上评估了我们的方法，并与在未受控场景中重建透明物体的最先进方法[Li et al. 2020]进行了比较。值得注意的是，他们的方法需要更复杂的设置，包括预先捕获环境图并手动标注每个视角的物体轮廓。其他透明物体重建方法专注于在具有设计图案的高度受控场景中进行重建[Lyu et al. 2020; Wu et al. 2018; Xu et al. 2022]，这些方法不适合与我们的方法进行公平比较。我们在补充材料中与[Lyu et al. 2020]在合成数据上进行了比较以供参考。最近，一种折射新视角合成方法被提出，通过eikonal场近似折射，并且仅以RGB图像作为输入[Bemana et al. 2022]。然而，我们通过实验发现它无法处理复杂透明物体中常见的全内反射，因此不能应用于透明物体重建。Bemana等人的方法在我们的实验中为大多数物体生成了不真实的结果。我们在补充材料中展示了他们的结果并进行了详细讨论。

4.1 实现细节

图9：真实数据的捕获图像。图像经过裁剪以便更好地可视化。

我们遵循[Wang et al. 2021]中的网络结构和位置编码。我们假设感兴趣区域位于单位球体内，并使用NeRF++[Zhang et al. 2020]处理球体外的场景。我们保持与[Wang et al. 2021]中相同的采样点数用于轮廓估计。对于使用估计轮廓进行形状初始化，我们设置迭代次数为100k，并添加eikonal项以正则化SDF场。轮廓损失和eikonal损失的权重均为1.0。对于基于折射渲染的形状优化，我们为粗采样采样16个点，为细采样采样另外16个点。每批次采样1024条射线用于渲染损失，256条射线用于轮廓损失，并优化模型300k次迭代。高斯模糊中的σ初始设置为10，每30k次迭代减半。形状优化在单个NVIDIA RTX4090 GPU上耗时约4小时，整个过程耗时11小时。对于真实数据采集，我们通过围绕物体拍摄大约40-50张RGB图像。部分图像如图9所示。然后我们使用COLMAP[Schonberger and Frahm 2016]获取相机参数。平面的位置通过使用RANSAC拟合从运动恢复的稀疏3D点计算得出。

4.2 合成数据结果

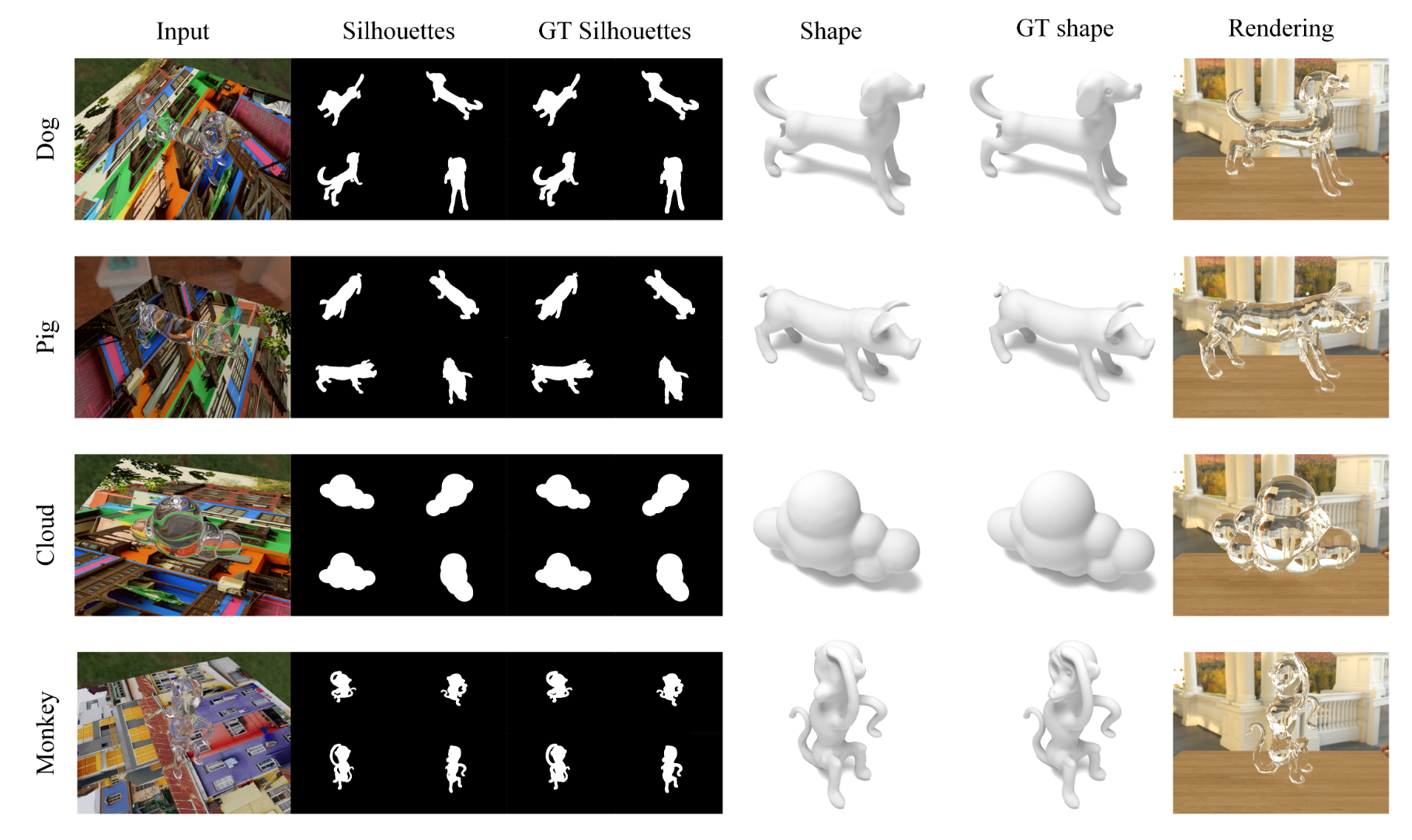
图6：我们在合成数据上的结果。我们展示了一些估计的轮廓和恢复的物体形状，并与真实值进行了比较。“输入”显示了其中一张输入多视角图像。我们恢复的轮廓和形状都非常准确。我们还在新环境中展示了重建结果的渲染图像。

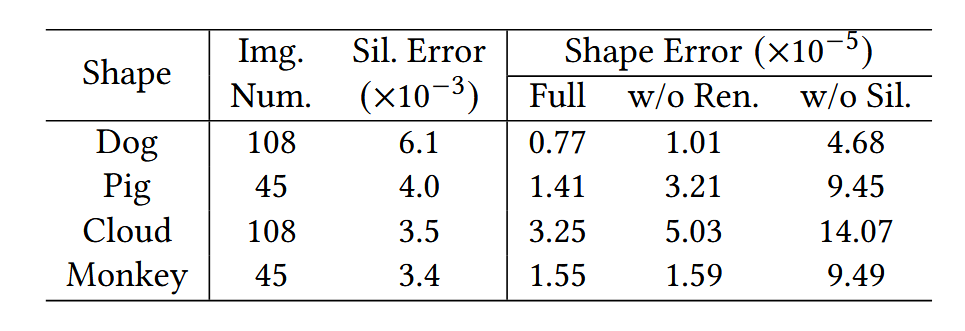
表1：我们在合成数据上的定量结果，包括输入图像数量、通过平均绝对误差（MAE）测量的轮廓误差、我们完整方法的形状重建误差、没有渲染损失的方法以及没有轮廓损失的方法。形状误差通过Chamfer距离测量，并通过包围盒对角线归一化。

我们在Mitsuba[Nimier-David et al. 2019]中渲染合成数据以评估我们的方法。透明物体的形状来自在线资源和[Lyu et al. 2020]中的数据，折射率设置为1.5。我们在优化中将初始折射率设置为$IoR_{init} = 1.6$，以验证其处理未知折射率的能力。平面的纹理来自[Agustsson and Timofte 2017]。我们从物体网络$N_o$中提取显式网格，并计算与真实形状的Chamfer距离以测量重建误差。我们展示了包含不同数量图像的合成样本，以证明我们方法的泛化能力。如图6所示，我们的方法为所有样本生成了高质量的结果。估计的多视角轮廓接近真实值，这证明了我们轮廓估计方法的优越性。此外，我们的方法重建了准确的物体形状。定量结果总结在表1中。

4.3 真实数据结果

图7：我们展示了在真实数据上的重建结果及其渲染效果，以便进行全面比较。与[Li et al. 2020]相比，我们的方法准确捕捉了物体的细节，如红框所示，且无需轮廓作为输入。

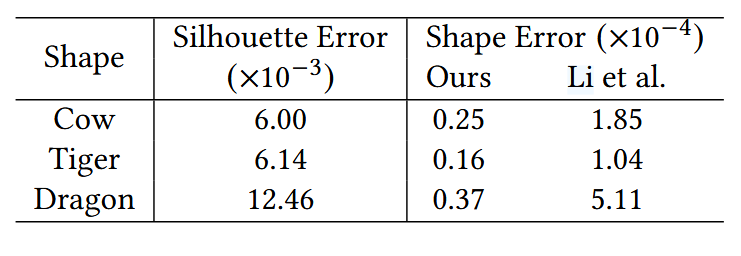
表2：我们在真实数据上的定量结果，与[Li et al. 2020]进行了比较。真实轮廓是通过在真实拍摄条件下渲染真实形状获得的。轮廓误差通过平均绝对误差（MAE）测量，形状误差通过Chamfer距离测量，并通过包围盒对角线归一化。

我们在三种真实透明物体上评估了我们的方法，并与[Li et al. 2020]进行了比较。我们使用ICP将结果与真实形状对齐，这些真实形状是通过将这些透明物体喷涂DPT-5后用扫描仪扫描获得的。如图7所示，我们的方法重建的形状精确地保留了表面细节和薄结构，例如老虎腹部的褶皱、牛的尾巴和角以及龙的尾巴和胡须。相比之下，Li等人的方法产生了过于平滑的结果，缺乏细节。这可能归因于他们的方法依赖于数据先验，并且受到合成训练数据分布与真实数据之间差距的影响。表2中总结的定量结果也证明了我们方法的优越性。我们的方法在不需要轮廓作为输入的情况下，取得了比最先进方法更好的结果。

4.4 消融实验

表1：我们在合成数据上的定量结果，包括输入图像数量、通过平均绝对误差（MAE）测量的轮廓误差、我们完整方法的形状重建误差、没有渲染损失的方法以及没有轮廓损失的方法。形状误差通过Chamfer距离测量，并通过包围盒对角线归一化。

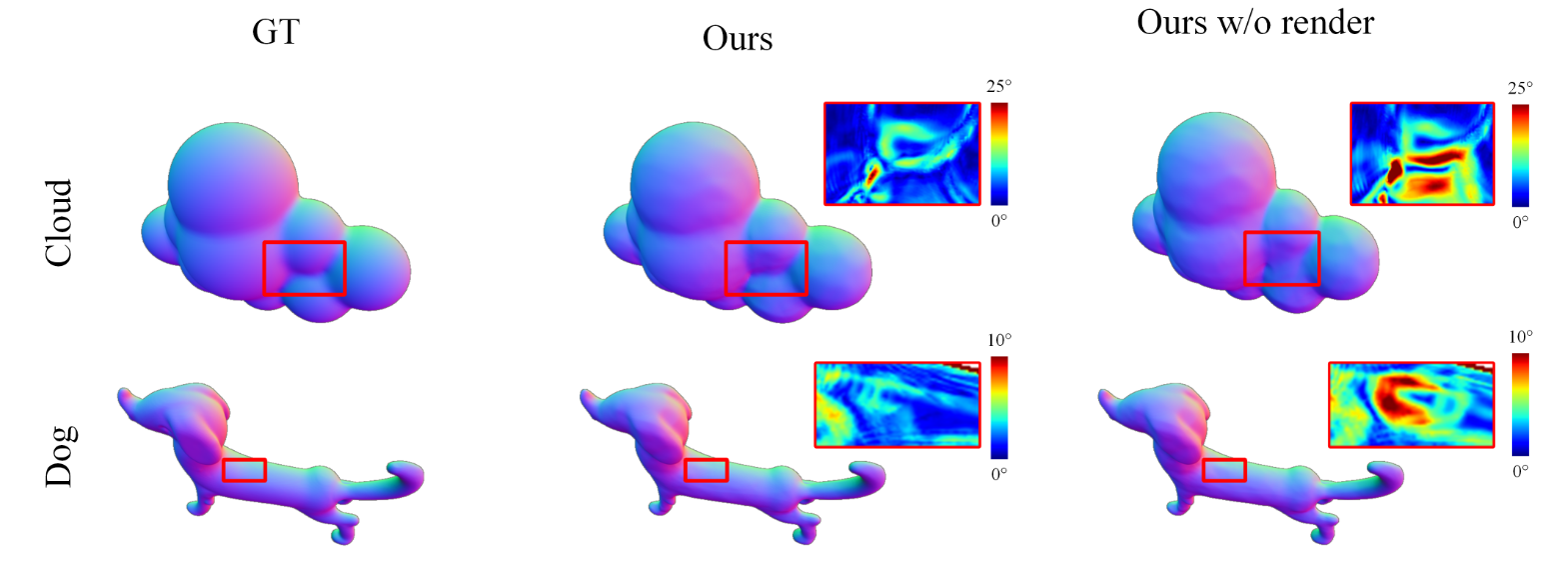
图8：消融实验的可视化结果。我们展示了真实形状的法线图、使用我们完整方法的结果以及没有渲染损失的结果。红框标记区域的角度误差（以度为单位）被放大并显示在右上角，其颜色条显示在上方。渲染损失显著改善了表面细节。

我们在合成数据上分别移除渲染损失和轮廓损失，以验证它们的效果。当移除轮廓损失时，物体形状无法保持正确的轮廓并表现出显著误差，如表1中的定量结果所示。我们还在图8中展示了没有渲染损失的结果，并与包含全部损失项恢复的形状进行了比较。如图8中的正常结果所示，“云”形状包含完全凹陷的区域（用红框标记），这些区域仅通过轮廓约束无法重建。没有渲染损失的优化会导致平坦的重建结果，而带有渲染损失的优化通过优化折射光路能够准确恢复形状。此外，有限数量的轮廓不足以完全约束物体的轮廓，渲染损失可以进一步优化凸区域，如图8中的“狗”形状。定量结果总结在表1中。

5 局限性与未来工作

图7：我们展示了在真实数据上的重建结果及其渲染效果，以便进行全面比较。与[Li et al. 2020]相比，我们的方法准确捕捉了物体的细节，如红框所示，且无需轮廓作为输入。

图10：失败案例。我们重建的真实物体“老虎”前脚的放大显示。由于缺乏折射畸变，我们的方法丢失了靠近平面的部分。

图6：我们在合成数据上的结果。我们展示了一些估计的轮廓和恢复的物体形状，并与真实值进行了比较。“输入”显示了其中一张输入多视角图像。我们恢复的轮廓和形状都非常准确。我们还在新环境中展示了重建结果的渲染图像。

尽管我们的方法能够生成高质量的结果，但在恢复透明物体与底层平面之间的接触区域（如图7和图10中物体的底部）时存在局限性。这主要是因为这些靠近平面的部分折射畸变较少，在场景重建中难以区分。此外，击中平面的折射光线数量不足以及颜色监督的模糊性会干扰优化过程，使得一些细节难以恢复（如图6中的猴子眼睛和图7中牛块上的条纹）。

6 结论

在本文中，我们提出了据我们所知第一种在不受控制的自然场景中重建透明物体的方法，且无需输入物体轮廓，这大大简化了透明物体重建的设置。我们将通过体渲染恢复的神经场投影回2D图像，以估计准确的多视角物体轮廓，并进一步执行隐式折射渲染，以重建由神经SDF场表示的详细形状。我们的方法简化了设置，能够在几分钟内完成完整的数据采集，这极大地促进了透明物体重建的实际应用。

致谢

本工作部分得到了中国国家重点研发计划（2022YFF0904301）的支持。

附录

图7：我们展示了在真实数据上的重建结果及其渲染效果，以便进行全面比较。与[Li et al. 2020]相比，我们的方法准确捕捉了物体的细节，如红框所示，且无需轮廓作为输入。

图8：消融实验的可视化结果。我们展示了真实形状的法线图、使用我们完整方法的结果以及没有渲染损失的结果。红框标记区域的角度误差（以度为单位）被放大并显示在右上角，其颜色条显示在上方。渲染损失显著改善了表面细节。

图9：真实数据的捕获图像。图像经过裁剪以便更好地可视化。

图10：失败案例。我们重建的真实物体“老虎”前脚的放大显示。由于缺乏折射畸变，我们的方法丢失了靠近平面的部分。

附录包含图7、图8、图9、图10。

通过隐式可微折射渲染实现透明物体重建 - 补充材料 -

高方舟，张梁浩，王莉，程嘉敏，张佳婉†

天津大学，中国

gaofangzhou@tju.edu.cn，opoiuiouiuy@tju.edu.cn，li_wang@tju.edu.cn，cjm@tju.edu.cn，jwzhang@tju.edu.cn

ACM引用格式：

高方舟，张梁浩，王莉，程嘉敏，张佳婉. 2023. 通过隐式可微折射渲染实现透明物体重建 - 补充材料 -. 收录于《2023年亚太计算机图形学大会（SIGGRAPH Asia 2023）会议论文集》（SA会议论文‘23），2023年12月12 - 15日，澳大利亚新南威尔士州悉尼. 美国计算机协会（ACM），美国纽约州纽约市，2页. https://doi.org/10.1145/3610548.3618236

1 与程函场的比较

最近，Bemana等人[2022]提出了一种用于折射新视图合成的新方法，该方法也以多视图RGB图像作为输入，并考虑了折射光线。由于他们的方法无法处理单位球体外部的场景，我们在一个纹理丰富的盒子内渲染透明物体。真实物体的边界框已给出。

图1：[Bemana等人，2022]在合成数据“猪”上的结果。我们展示了他们在两个新视图上的视图合成结果，并与作为参考的真实情况进行比较。形状是通过移动立方体算法从他们的程函场中提取出来的，并手动设置了最优阈值。

Bemana等人利用程函场来表示场景中各点的折射率（IoR），以实现光线折射的模拟。然而，他们的方法在优化过程中没有考虑全反射引起的高光效果。因此，在处理复杂物体时，无法提供合理的结果。如图1所示，从正面观察时，猪头布满高光，而他们的方法得出的结果并不真实。相比之下，正如论文主体部分所述，我们的方法能够重建出可靠的结果。

图3：[Bemana等人，2022]在合成数据“球”上的结果。左侧是他们的视图合成结果。右侧，我们展示了球的横截面上的折射率（IoR）分布，并在下方提供了一个色条作为参考。

此外，程函场的高度自由度常常使其无法收敛到准确的表示。如图3所示，尽管Bemana等人的方法生成的图像看似合理，但程函场覆盖的是一个折射率逐渐变化的场，而不是一个具有清晰边界的均匀实体。这在使用移动立方体算法（marching cubes algorithm）提取准确几何形状时，在设置合适的阈值方面带来了挑战。

2 与DRT方法的比较

我们还将我们的方法与[Lyu等人，2020]的方法进行了比较，后者在高度受控的场景中重建透明物体，使用合成数据作为参考。他们的方法需要大约1500张通过显示格雷码的屏幕拍摄的图像，以重建出详细的形状。

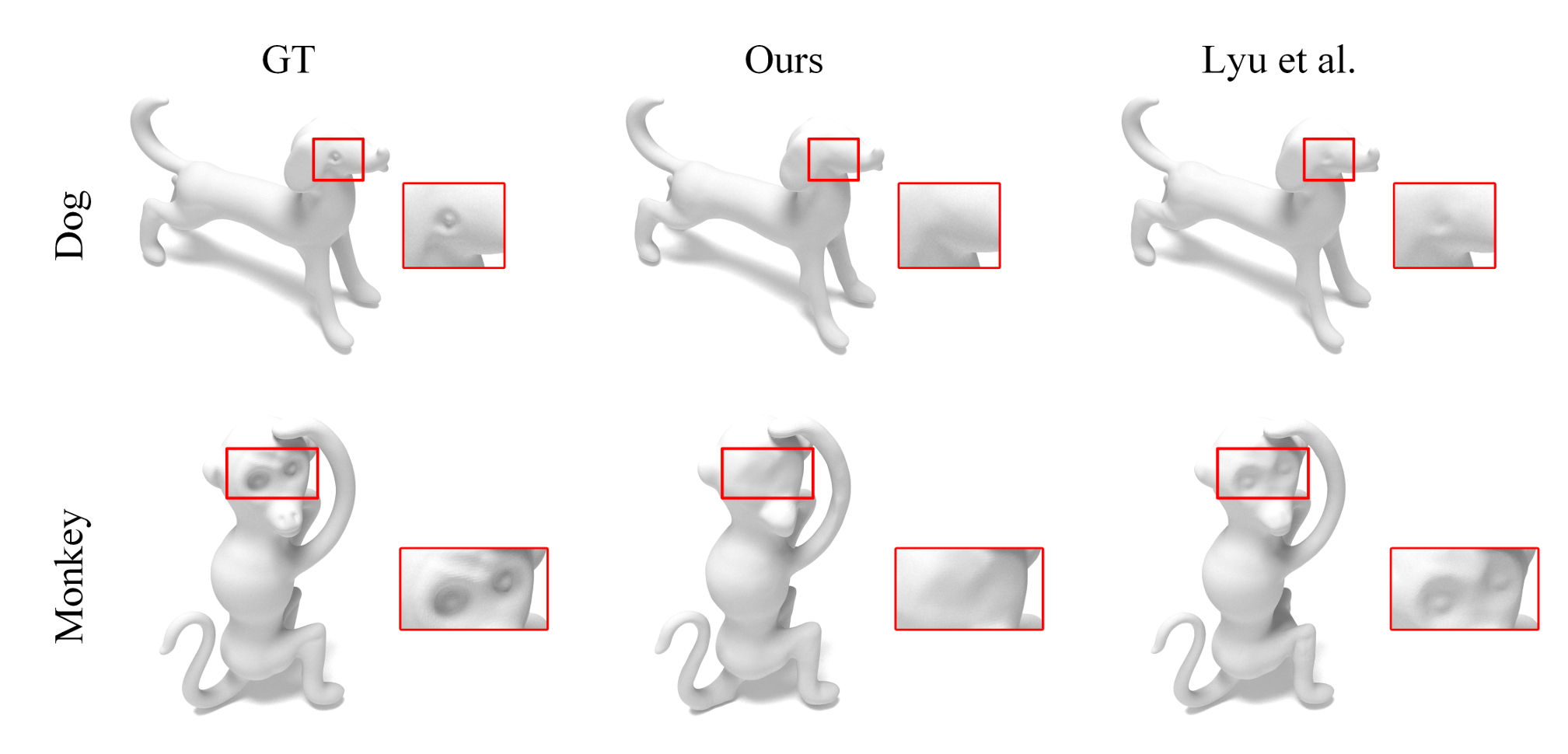
图2：我们的方法与[Lyu等人，2020]方法的比较。两种方法都能重建出整体精确的形状，而Lyu等人的方法在受限的设置下能够重建出更细节的眼睛（用红色框标记）。

我们在合成的透明物体上运行他们的方法，输入图像是按照他们的设置渲染的。比较结果如图2所示。两种方法重建的形状在整体上都接近真实形状，而他们的方法由于设置更为受限，能够恢复更多的局部细节。

致谢

本研究工作部分得到了中国国家重点研发计划（2022YFF0904301）的支持。