标题
Marching cubes: A high resolution 3D surface construction algorithm
1987, ACM SIGGRAPH Computer Graphics, 18320 citations.
链接
论文链接:
代码实现:原论文中提到,代码使用C语言实现。目前已经有Python版本的代码实现,同时也是NeRF在GitHub代码中引用的实现库,PyMCubes。
NeRF中采用的提取Mesh代码:
NeRF的GitHub链接:
此前我的NeRF阅读笔记:
作者
William E. Lorensen, Harvey E.Cline
General Electric Company
Corporate Research and Development
Schenectady, New York 12301
1987年,通用电力公司的两个研发部门的大佬写的文章。
要点
目的
我们假定空间中的每个位置都有一些属性值,可以通过这些数值来判断空间中的该点处于物体的内部还是外部。
在给定空间中的数值后,希望找到物体的三维轮廓边界,也就是物体的外表面。
最后,需要将外表面表示为计算机可以体现的模式,Mesh网格。也就是将物体的外表面三角面片化,得到最后面片化的网格顶点及三角面片。
思想
-
首先设想一片纯白的空间,这片纯白的空间正中央只有一个沙发。
-
接下来,把这片空间切成无数长宽高相等的小立方体,沙发的表面会与每个小立方体有相交的地方。有许多小立方体划分到沙发内部;一些小立方体和沙发表面有交集;另一些小立方体完全与沙发不相交,在纯白空间中的其他地方。
- 随后,考虑与沙发的表面有相交的立方体。一个正方体,有8个顶点以及12条边,物体的表面可能与正方体有各种形式的相交办法。
- 我们这样简化思考:正方体的8个顶点,每个顶点要么在物体表面的内部,要么在物体表面的外部,要么恰好在物体的表面之上。
- 将这三种情况简化成两种,立方体的每个顶点,要么在物体表面的内部,要么在物体表面的外部或者恰好在表面上。
- 如果顶点在物体内部,我们给顶点赋值为1;如果顶点在物体外部或者物体内部,我们给该顶点赋值为0。
- 这样,按照立方体处于物体的表面内部还是外部,就产生了$2^{8}=256$种可能的状态。
- 这$2^{8}=256$种状态,存在许多可以合并的状态。做如下两种简化:
- 简化一,顶点在物体内部赋值为0还是1,并不影响表面是如何与正方体相交的。因此,将0和1翻转过来,两类表示是相同的。256种状态合并为128种状态。
- 简化二,如果给这些立方体做旋转,几种状态是可以合并的。
- 经过这两种简化,物体与立方体的相交,简化为14种状态,以及1种完全不相交的状态。
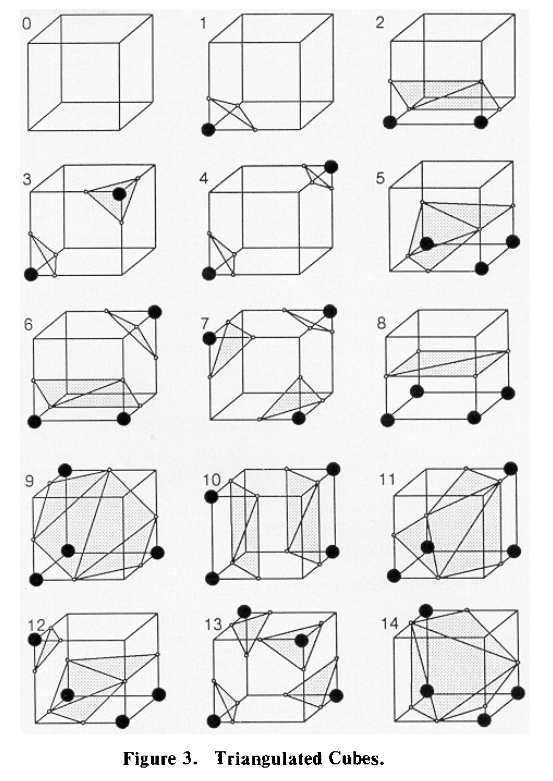
- 注意到,这里的所有状态,只有0-4个三角面片,没有更多三角面片了。
- 随后,作者将这256种状态,与其状态对应的三角面片的形成方案相对应,形成索引表。每个顶点有2种状态,可用一个bit表示;8个顶点对应8bit,也就是一个字节。此后,只要查索引表,就可形成对应的mesh结构。
- 最后,要线性插值得到三角面片的顶点位置,以及顶点所对应的法向量。
方法
文中给出了两种优化。
- 计算法向量的时候,每个三角面片的顶点,在cubes被marching之后,只有3条新的边需要重新计算。经过缩减计算时间,三角面片的每个顶点,应该只需要计算一次。
- 多个表面相交的时候,立方体在不同表面内部、外部的时候,给出一张真值表,提供具体生成三角面片的方案。
想法
优点
- 思想简洁。
- 实现高效。构建索引表、每次只计算新的三个边,都是好的优化策略。
缺点
- 距离当下的时间有些远,具体的细节还不太清楚。
评论